北师大版五年级上册数学4.3 平行四边形的面积 课件 (共14张PPT)
文档属性
| 名称 | 北师大版五年级上册数学4.3 平行四边形的面积 课件 (共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 263.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-03 08:30:06 | ||
图片预览



文档简介
(共14张PPT)
平行四边形的面积
《多边形的面积》第3课时
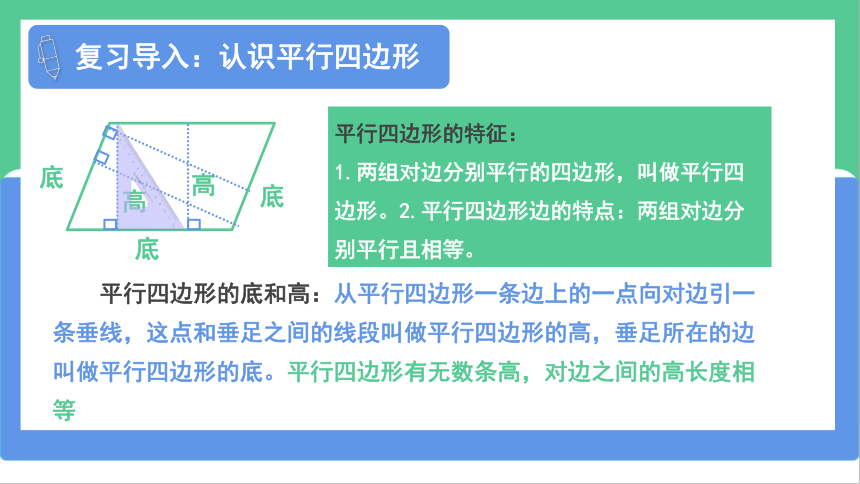
复习导入:认识平行四边形
平行四边形的底和高:从平行四边形一条边上的一点向对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高,垂足所在的边叫做平行四边形的底。平行四边形有无数条高,对边之间的高长度相等
底
底
底
高
高
平行四边形的特征:
1.两组对边分别平行的四边形,叫做平行四边形。2.平行四边形边的特点:两组对边分别平行且相等。
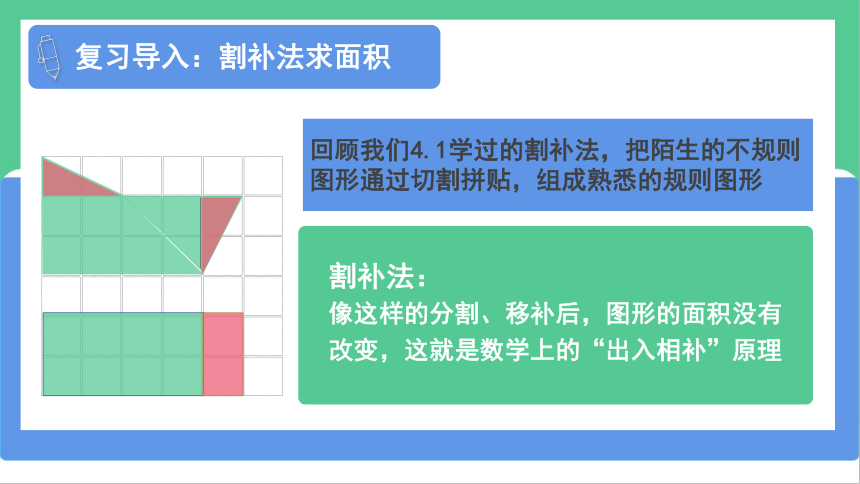
复习导入:割补法求面积
割补法:
像这样的分割、移补后,图形的面积没有改变,这就是数学上的“出入相补”原理
回顾我们4.1学过的割补法,把陌生的不规则图形通过切割拼贴,组成熟悉的规则图形
思考,平行四边形能否通过切割拼贴,组成其他规则图形?多边形面积如何计算?
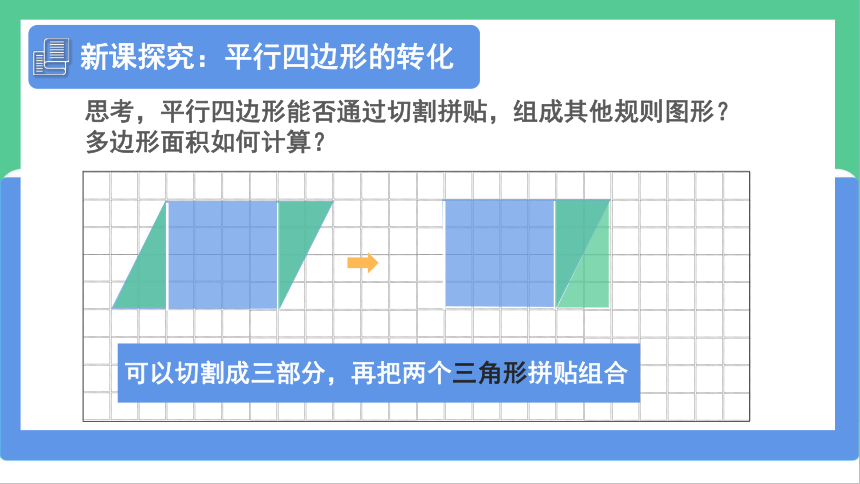
新课探究:平行四边形的转化
可以切割成三部分,再把两个三角形拼贴组合
我们发现:
沿高把平行四边形分成三部分(两个三角形+一个矩形),通过平移或旋转(把两个三角形拼接成矩形),可以转化成长方形。
新课探究:平行四边形的转化
思考:有没有其他方法?
思考,平行四边形能否通过切割拼贴,组成其他规则图形?多边形面积如何计算?
可以切割成三部分,再把两个梯形拼贴组合
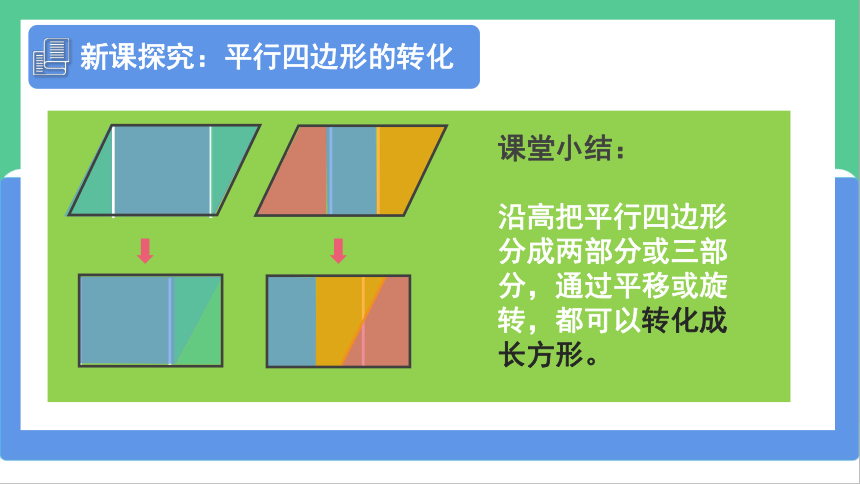
新课探究:平行四边形的转化
课堂小结:
沿高把平行四边形分成两部分或三部分,通过平移或旋转,都可以转化成长方形。
新课探究:平行四边形的转化
新课探究:平行四边形的面积
平行四边形的底和高
底:4+2
高:4
长方形的长和宽
底:4+2
高:4
新课探究:平行四边形的面积
平行四边形的底边
平行四边形的高
长方形的长
长方形的宽
=
平行四边形的面积
长方形的面积
=
面积=长×宽
面积=底×高
=
所以,平行四边形面积=底×高. 用字母表示就是S= a×h.
新课探究:平行四边形的面积
课堂小结:
1.沿高把平行四边形分成两部分或三部分,通过平移或旋转,都可以转化成长方形。
2.平行四边形的面积=底×高;字母表达式:S= ɑ × h 。已知平行四边形的底、高和面积三个量中的任意两个量,都可以求出第三个量。即 S= ɑ × h,a=s÷h,h=s÷a.
课堂练习:学以致用
1.已知平行四边形的底是5.8米,高是0.6米,求面积
2.平行四边形的底是10米,高是16米, 求面积?
3.一个平行四边形的底是5分米,高是0.5厘米,求面积?
4.平行四边形的底和高分别与长方形的长和宽相等,它们的面积一定相等吗?为什么?
课堂练习:学以致用
5.一块平行四边形菜地,底是30米,高是15米每平方米收青菜4千克。这块地共可收青菜多少千克?
6.一块平行四边形的草地,底是18米,高是10米.这块草地的面积是多少?
课堂练习:学以致用
任意一个平行四边形都可以转化成一个( ),它的面积与原平行四边形的面积( )。这个长方形的长与原平行四边形的( )相等。这个长方形的( )与原平行四边形的( )相等。因为长方形的面积等于( ),所以平行四边形的面积等于( ) 。
长方形
相等
底
宽
高
长×宽
底×高
谢谢观看
平行四边形的面积
《多边形的面积》第3课时
复习导入:认识平行四边形
平行四边形的底和高:从平行四边形一条边上的一点向对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高,垂足所在的边叫做平行四边形的底。平行四边形有无数条高,对边之间的高长度相等
底
底
底
高
高
平行四边形的特征:
1.两组对边分别平行的四边形,叫做平行四边形。2.平行四边形边的特点:两组对边分别平行且相等。
复习导入:割补法求面积
割补法:
像这样的分割、移补后,图形的面积没有改变,这就是数学上的“出入相补”原理
回顾我们4.1学过的割补法,把陌生的不规则图形通过切割拼贴,组成熟悉的规则图形
思考,平行四边形能否通过切割拼贴,组成其他规则图形?多边形面积如何计算?
新课探究:平行四边形的转化
可以切割成三部分,再把两个三角形拼贴组合
我们发现:
沿高把平行四边形分成三部分(两个三角形+一个矩形),通过平移或旋转(把两个三角形拼接成矩形),可以转化成长方形。
新课探究:平行四边形的转化
思考:有没有其他方法?
思考,平行四边形能否通过切割拼贴,组成其他规则图形?多边形面积如何计算?
可以切割成三部分,再把两个梯形拼贴组合
新课探究:平行四边形的转化
课堂小结:
沿高把平行四边形分成两部分或三部分,通过平移或旋转,都可以转化成长方形。
新课探究:平行四边形的转化
新课探究:平行四边形的面积
平行四边形的底和高
底:4+2
高:4
长方形的长和宽
底:4+2
高:4
新课探究:平行四边形的面积
平行四边形的底边
平行四边形的高
长方形的长
长方形的宽
=
平行四边形的面积
长方形的面积
=
面积=长×宽
面积=底×高
=
所以,平行四边形面积=底×高. 用字母表示就是S= a×h.
新课探究:平行四边形的面积
课堂小结:
1.沿高把平行四边形分成两部分或三部分,通过平移或旋转,都可以转化成长方形。
2.平行四边形的面积=底×高;字母表达式:S= ɑ × h 。已知平行四边形的底、高和面积三个量中的任意两个量,都可以求出第三个量。即 S= ɑ × h,a=s÷h,h=s÷a.
课堂练习:学以致用
1.已知平行四边形的底是5.8米,高是0.6米,求面积
2.平行四边形的底是10米,高是16米, 求面积?
3.一个平行四边形的底是5分米,高是0.5厘米,求面积?
4.平行四边形的底和高分别与长方形的长和宽相等,它们的面积一定相等吗?为什么?
课堂练习:学以致用
5.一块平行四边形菜地,底是30米,高是15米每平方米收青菜4千克。这块地共可收青菜多少千克?
6.一块平行四边形的草地,底是18米,高是10米.这块草地的面积是多少?
课堂练习:学以致用
任意一个平行四边形都可以转化成一个( ),它的面积与原平行四边形的面积( )。这个长方形的长与原平行四边形的( )相等。这个长方形的( )与原平行四边形的( )相等。因为长方形的面积等于( ),所以平行四边形的面积等于( ) 。
长方形
相等
底
宽
高
长×宽
底×高
谢谢观看
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
