高中数学必修第一册人教A版(2019)3.4《函数的应用(一)》名师课件(共29张PPT)
文档属性
| 名称 | 高中数学必修第一册人教A版(2019)3.4《函数的应用(一)》名师课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-03 00:00:00 | ||
图片预览






文档简介
(共29张PPT)
人教A版同步教材名师课件
函数的应用(一)
学习目标
学 习 目 标 核心素养
掌握一次函数、二次函数、分段函数的函数模型及其特点 数学建模
掌握幂函数的实际应用 数学运算
能根据题意建立函数关系,并能利用函数模型解决实际问题 数学建模
课程目标
1、能够找出简单实际问题中的函数关系式,初步体会应用一次函数、二次函数、幂函数、分段函数模型解决实际问题;
2、感受运用函数概念建立模型的过程和方法,体会一次函数、二次函数、幂函数、分段函数模型在数学和其他学科中的重要性.
数学学科素养
1、数学抽象:总结函数模型;
2、逻辑推理:找出简单实际问题中的函数关系式,根据题干信息写出分段函数;
3、数学运算:结合函数图象或其单调性来求最值;
4、数据分析:二次函数通过对称轴和定义域区间求最优问题;
5、数学建模:在具体问题情境中,运用数形结合思想,将自然语言用数学表达式表示出来.
学习目标
探究新知
(1)一次函数模型:( 为常数,),也称线性函数模型.
(2)二次函数模型:当研究的问题呈现先增长后减少的特点时,可以选用二次函数模型( 为常数, );当研究的问题呈现先减少后增长的特点时,可以选用二次函数模型( 为常数, ).
(3)幂函数模型:(为常数, , ).
(4)反比例函数模型:(为常数,).
(5)分段函数模型:一种比较复杂的函数模型,可以用来描述在不同区间上有不同变化规律的实际问题.或者将定义域上变化复杂的函数分成几段区间来研究,在每一段区间上函数有各自的变化规律,根据函数的具体变化,再分段选择相应的函数模型.
常见的几种函模型:
探究新知
(1)审题:弄清题意,分清条件和结论,理清数量关系,初步选择模型.
(2)建模:将自然语言转化为数学语言,利用数学知识,建立相应的函数模型.
(3)求解:根据实际问题所需要解决的目标及函数式的结构特征正确求得函数模型的解.
(4)还原:应用问题不是单纯的数学问题,既要符合数学学科背景又要符合实际背景,因此解出的结果要代入原问题中进行检验、评判,最后得出结论,作出回答.
实际问题中函数建模的基本步骤:
探究新知
(1)通过实际问题抽象函数模型时,有时需要用待定系数法、归纳法等方法确定函数关系式.
(2)确定的函数关系式不一定符合实际情况,还需要进行检验.
(3)要熟知各类函数模型的增长或减少的变化情况,如一次函数模型是恒增或恒减的,二次函数模型是先增后减或先减后增等.
①
典例讲解
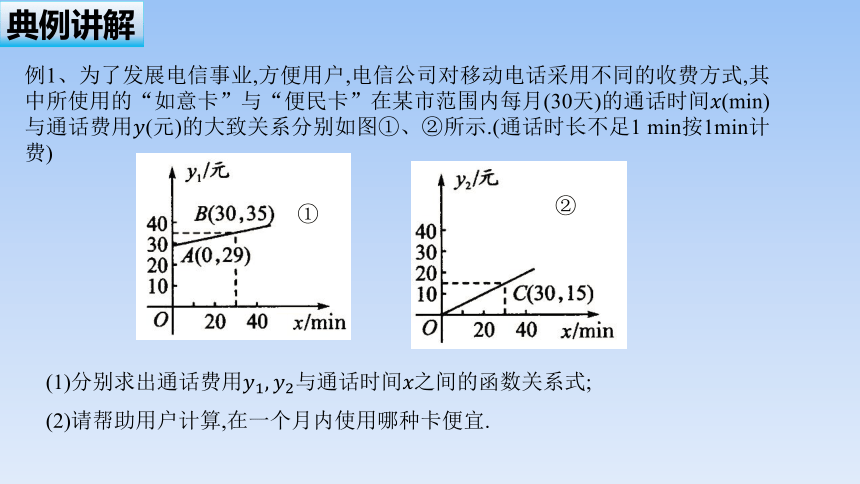
例1、为了发展电信事业,方便用户,电信公司对移动电话采用不同的收费方式,其中所使用的“如意卡”与“便民卡”在某市范围内每月(30天)的通话时间(min)与通话费用(元)的大致关系分别如图①、②所示.(通话时长不足1 min按1min计费)
②
(1)分别求出通话费用与通话时间之间的函数关系式;
(2)请帮助用户计算,在一个月内使用哪种卡便宜.
①
典例讲解
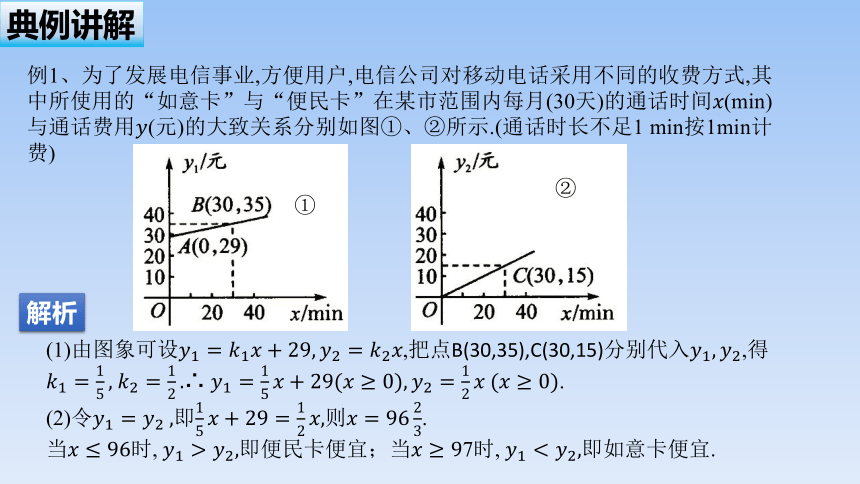
例1、为了发展电信事业,方便用户,电信公司对移动电话采用不同的收费方式,其中所使用的“如意卡”与“便民卡”在某市范围内每月(30天)的通话时间(min)与通话费用(元)的大致关系分别如图①、②所示.(通话时长不足1 min按1min计费)
②
(1)由图象可设,把点B(30,35),C(30,15)分别代入,得 ∴ .
(2)令即则.
当时, 即便民卡便宜;当7时, 即如意卡便宜.
解析
方法归纳
变式训练
1.某列火车从北京西站开往石家庄,全程277 km.火车出发10 min开出13km,之后以120 km/h的速度匀速行驶.试写出火车行驶的总路程s与匀速行驶的时间t之间的函数关系式,并求离开北京2h时火车行驶的路程.
因为火车匀速行驶的总时间为(277-13)÷120(h),所以 . 因为火车匀速行驶th所行驶的路程为km,所以火车行驶的总路程与匀速行驶的时间之间的函数关系式为. 离开北京2h时火车匀速行驶的时间为2 (h),此时火车行驶的路程(km).
解析
典例讲解
例2、一辆汽车在某段路程中行驶的平均速率(单位:km/h)与时间(单位:h)的关系如图所示.
(1)求图中阴影部分的面积,关说明所求面积的实际含义;
(2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004km,试建立汽车行驶这段路程时汽车里程表读数与时间的函数解析式,并作出相应的图象.
解析
(1)阴影部分的面积为.
阴影部分的面积表示汽车在这5 h内行驶的路程为360km.
典例讲解
解析
(2)根据题意得:图象如右图示.
例2、一辆汽车在某段路程中行驶的平均速率(单位:km/h)与时间(单位:h)的关系如图所示.
(1)求图中阴影部分的面积,关说明所求面积的实际含义;
(2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004km,试建立汽车行驶这段路程时汽车里程表读数与时间的函数解析式,并作出相应的图象.
方法归纳
(1)在函数定义域内,根据自变量取值范围的不同,由题设确定出不同的函数解析式.
(2)应用分段函数模型的关键是确定各段的边界点,即明确自变量的取值区间,从而写出函数解析式.特别注意,分段函数的最值是整个定义域上的最值.
(3)要注意结合实际问题的意义,有时还可结合图象去求解.
变式训练
2.经市场调查,某门市部的一种小商品在过去的20天内的日销售量(件)与销售价格(元)均为关于时间(天)的函数,日销售量近似满足函数,销售价格近似满足函数
(1)试写出该种商品的日销售额与时间的函数表达式;
(2)求该种商品的日销售额的最大值.
解析
(1)由已知得即
变式训练
2.经市场调查,某门市部的一种小商品在过去的20天内的日销售量(件)与销售价格(元)均为关于时间(天)的函数,日销售量近似满足函数,销售价格近似满足函数
(1)试写出该种商品的日销售额与时间的函数表达式;
(2)求该种商品的日销售额的最大值.
解析
(2)由(1)知,①当时,[0,5]上递增,在(5,10]上递减,∴(当=5时取得).
②当时,在(10,20]上递减,∴.
由①②知.故该种商品的日销售额的最大值为1225元.
例3、某个体经营者把前六个月试销A,B两种商品的逐月投资与所获纯利润制成下表:
该经营者准备下个月投入12万元经营这两种商品,但不知投入A,B两种商品各多少万元才最合算.请你帮他制订一个资金投入方案,使得该经营者能获得最大纯利润,并求出最大纯利润.(均精确到0.1万元)
以投资额为横坐标,纯利润为纵坐标,画出散点图,如图所示:
解析
典例讲解
例3、某个体经营者把前六个月试销A,B两种商品的逐月投资与所获纯利润制成下表:
解析
典例讲解
据此,可考虑用函数 ①表示投资A种商品的金额与其纯利润的关系,用函数 ②表示投资B种商品的金额与其纯利润的关系.
把代入①式,得0.65,解得,经检验,解析式基本满足题意,故所获纯利润关于月投资A种商品的金额的函数解析式可近似地用来表示.
把代入②式,解得,经检验,解析式基本满足题意,故所获纯利润关于月投资B种商品的金额的函数解析式可近似地用来表示.
例3、某个体经营者把前六个月试销A,B两种商品的逐月投资与所获纯利润制成下表:
解析
典例讲解
设下个月投入A,B两种商品的资金分别是万元、 万元,纯利润为W万元,得
即.
故当时,取得最大值,约为4.1.此时,.即下个月投入A,B两种商品的资金分别约为3.2万元、8.8万元时,可获得最大纯利润,约为4.1万元.
方法归纳
二次函数模型主要用来解决实际问题中的利润最大、用料最省等问题,是高考考查的重点.解题时,建立二次函数解析式后,可以利用配方法、判别式法、换元法、函数的单调性等来求函数的最值,从而解决实际问题.
3.某汽车租赁公司拥有汽车100辆.每辆车的月租金为3000元时,可全部租出,每辆车的月租金每增加50元,未租出的车就会增加一辆租出的车每辆每月需要维护费150元,未租出的车每辆每月要维护费50 元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
解析
(1)当每辆车的月租金定为3600元时,未租出的车辆数为,所以这时租出了辆车.
(2)设每辆车的月租金定为元,租赁公司的月收益为元,
则
所以
所以,当时,最大,其最大值为307050.
因此当每辆车的月租金定为4050元时,租赁公司的月收益最大,最大月收益为307050元.
变式训练
典例讲解
例4、某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元.
(1)分别写出两类产品的收益与投资额的函数关系式;
(2)该家庭现有20万元资金,全部用于理财投资,怎么分配资金能使投资获得最大收益?最大收益是多少万元?
解析
(1)设两类产品的收益与投资额的函数关系式分别为:
,从而有,
所以.
典例讲解
例4、某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元.
(1)分别写出两类产品的收益与投资额的函数关系式;
(2)该家庭现有20万元资金,全部用于理财投资,怎么分配资金能使投资获得最大收益?最大收益是多少万元?
解析
(2)设投资债券产品万元,则股票类投资为万元,获得的收益为万元.
令,则,
所以当,即时,取得最大值, .所以当投资债券16万元,投资股票4万元时,能获得最大收益,最大收益是3万元.
方法归纳
(1)给出含参数的函数关系式,利用待定系数法求出参数,确定函数关系式.
(2)根据题意,直接列出相应的函数关系式.
幂函数模型应用的求解策略
变式训练
4.在固定压力差(压力差为常数)下,当气体通过圆形管道时,其流量速度与管道半径的四次方成正比.
(1)若气体在半径为的管道中,流量速度为400,求该气体通过半径为r的管道时,其流量速度的函数解析式;
(2)已知(1)中的气体通过的管道半径为,计算该气体的流量速度(保留一位小数).
(1)设.
因为当时,,所以,故所求函数解析式为.
(2)当时,该气体的流量速度为.
解析
当堂练习
1.某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,开源节流,现要从这些边角料上截取矩形铁片(如图中阴影部分)备用,当截取的矩形面积最大时,矩形两边长应为( )
A. B. C. D.
A
当堂练习
2.加工爆米花时,爆开且不娴的粒数占加工总粒数的百分比称为“可食用率”.在特定条件下,可食用率与加工时间(单位:分钟)满足函数关系是常数),如图记录了三次试验的数据.根据上述函数模型和试验数据,可以得到最佳加工时间为( )
A.分钟 B. 分钟 C. D.
B
当堂练习
3.国家规定个人稿费的纳税办法是:不超过800元的不纳税;超过800而不超过4000元的按超过800元部分的14%纳税;超过4000元的按全部稿酬的11%纳税,某人出版了一本书,共纳税420元,则这个人的稿费为 元.
4.现测得的两组对应值分别为(1,2),(2,5),现有两个待选模型,甲:,乙:,若又测得的一组对应值为(3,10.2),则应选用 作为函数模型.
3800
甲
归纳小结
作 业
教材P95练习:1、3
人教A版同步教材名师课件
函数的应用(一)
学习目标
学 习 目 标 核心素养
掌握一次函数、二次函数、分段函数的函数模型及其特点 数学建模
掌握幂函数的实际应用 数学运算
能根据题意建立函数关系,并能利用函数模型解决实际问题 数学建模
课程目标
1、能够找出简单实际问题中的函数关系式,初步体会应用一次函数、二次函数、幂函数、分段函数模型解决实际问题;
2、感受运用函数概念建立模型的过程和方法,体会一次函数、二次函数、幂函数、分段函数模型在数学和其他学科中的重要性.
数学学科素养
1、数学抽象:总结函数模型;
2、逻辑推理:找出简单实际问题中的函数关系式,根据题干信息写出分段函数;
3、数学运算:结合函数图象或其单调性来求最值;
4、数据分析:二次函数通过对称轴和定义域区间求最优问题;
5、数学建模:在具体问题情境中,运用数形结合思想,将自然语言用数学表达式表示出来.
学习目标
探究新知
(1)一次函数模型:( 为常数,),也称线性函数模型.
(2)二次函数模型:当研究的问题呈现先增长后减少的特点时,可以选用二次函数模型( 为常数, );当研究的问题呈现先减少后增长的特点时,可以选用二次函数模型( 为常数, ).
(3)幂函数模型:(为常数, , ).
(4)反比例函数模型:(为常数,).
(5)分段函数模型:一种比较复杂的函数模型,可以用来描述在不同区间上有不同变化规律的实际问题.或者将定义域上变化复杂的函数分成几段区间来研究,在每一段区间上函数有各自的变化规律,根据函数的具体变化,再分段选择相应的函数模型.
常见的几种函模型:
探究新知
(1)审题:弄清题意,分清条件和结论,理清数量关系,初步选择模型.
(2)建模:将自然语言转化为数学语言,利用数学知识,建立相应的函数模型.
(3)求解:根据实际问题所需要解决的目标及函数式的结构特征正确求得函数模型的解.
(4)还原:应用问题不是单纯的数学问题,既要符合数学学科背景又要符合实际背景,因此解出的结果要代入原问题中进行检验、评判,最后得出结论,作出回答.
实际问题中函数建模的基本步骤:
探究新知
(1)通过实际问题抽象函数模型时,有时需要用待定系数法、归纳法等方法确定函数关系式.
(2)确定的函数关系式不一定符合实际情况,还需要进行检验.
(3)要熟知各类函数模型的增长或减少的变化情况,如一次函数模型是恒增或恒减的,二次函数模型是先增后减或先减后增等.
①
典例讲解
例1、为了发展电信事业,方便用户,电信公司对移动电话采用不同的收费方式,其中所使用的“如意卡”与“便民卡”在某市范围内每月(30天)的通话时间(min)与通话费用(元)的大致关系分别如图①、②所示.(通话时长不足1 min按1min计费)
②
(1)分别求出通话费用与通话时间之间的函数关系式;
(2)请帮助用户计算,在一个月内使用哪种卡便宜.
①
典例讲解
例1、为了发展电信事业,方便用户,电信公司对移动电话采用不同的收费方式,其中所使用的“如意卡”与“便民卡”在某市范围内每月(30天)的通话时间(min)与通话费用(元)的大致关系分别如图①、②所示.(通话时长不足1 min按1min计费)
②
(1)由图象可设,把点B(30,35),C(30,15)分别代入,得 ∴ .
(2)令即则.
当时, 即便民卡便宜;当7时, 即如意卡便宜.
解析
方法归纳
变式训练
1.某列火车从北京西站开往石家庄,全程277 km.火车出发10 min开出13km,之后以120 km/h的速度匀速行驶.试写出火车行驶的总路程s与匀速行驶的时间t之间的函数关系式,并求离开北京2h时火车行驶的路程.
因为火车匀速行驶的总时间为(277-13)÷120(h),所以 . 因为火车匀速行驶th所行驶的路程为km,所以火车行驶的总路程与匀速行驶的时间之间的函数关系式为. 离开北京2h时火车匀速行驶的时间为2 (h),此时火车行驶的路程(km).
解析
典例讲解
例2、一辆汽车在某段路程中行驶的平均速率(单位:km/h)与时间(单位:h)的关系如图所示.
(1)求图中阴影部分的面积,关说明所求面积的实际含义;
(2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004km,试建立汽车行驶这段路程时汽车里程表读数与时间的函数解析式,并作出相应的图象.
解析
(1)阴影部分的面积为.
阴影部分的面积表示汽车在这5 h内行驶的路程为360km.
典例讲解
解析
(2)根据题意得:图象如右图示.
例2、一辆汽车在某段路程中行驶的平均速率(单位:km/h)与时间(单位:h)的关系如图所示.
(1)求图中阴影部分的面积,关说明所求面积的实际含义;
(2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004km,试建立汽车行驶这段路程时汽车里程表读数与时间的函数解析式,并作出相应的图象.
方法归纳
(1)在函数定义域内,根据自变量取值范围的不同,由题设确定出不同的函数解析式.
(2)应用分段函数模型的关键是确定各段的边界点,即明确自变量的取值区间,从而写出函数解析式.特别注意,分段函数的最值是整个定义域上的最值.
(3)要注意结合实际问题的意义,有时还可结合图象去求解.
变式训练
2.经市场调查,某门市部的一种小商品在过去的20天内的日销售量(件)与销售价格(元)均为关于时间(天)的函数,日销售量近似满足函数,销售价格近似满足函数
(1)试写出该种商品的日销售额与时间的函数表达式;
(2)求该种商品的日销售额的最大值.
解析
(1)由已知得即
变式训练
2.经市场调查,某门市部的一种小商品在过去的20天内的日销售量(件)与销售价格(元)均为关于时间(天)的函数,日销售量近似满足函数,销售价格近似满足函数
(1)试写出该种商品的日销售额与时间的函数表达式;
(2)求该种商品的日销售额的最大值.
解析
(2)由(1)知,①当时,[0,5]上递增,在(5,10]上递减,∴(当=5时取得).
②当时,在(10,20]上递减,∴.
由①②知.故该种商品的日销售额的最大值为1225元.
例3、某个体经营者把前六个月试销A,B两种商品的逐月投资与所获纯利润制成下表:
该经营者准备下个月投入12万元经营这两种商品,但不知投入A,B两种商品各多少万元才最合算.请你帮他制订一个资金投入方案,使得该经营者能获得最大纯利润,并求出最大纯利润.(均精确到0.1万元)
以投资额为横坐标,纯利润为纵坐标,画出散点图,如图所示:
解析
典例讲解
例3、某个体经营者把前六个月试销A,B两种商品的逐月投资与所获纯利润制成下表:
解析
典例讲解
据此,可考虑用函数 ①表示投资A种商品的金额与其纯利润的关系,用函数 ②表示投资B种商品的金额与其纯利润的关系.
把代入①式,得0.65,解得,经检验,解析式基本满足题意,故所获纯利润关于月投资A种商品的金额的函数解析式可近似地用来表示.
把代入②式,解得,经检验,解析式基本满足题意,故所获纯利润关于月投资B种商品的金额的函数解析式可近似地用来表示.
例3、某个体经营者把前六个月试销A,B两种商品的逐月投资与所获纯利润制成下表:
解析
典例讲解
设下个月投入A,B两种商品的资金分别是万元、 万元,纯利润为W万元,得
即.
故当时,取得最大值,约为4.1.此时,.即下个月投入A,B两种商品的资金分别约为3.2万元、8.8万元时,可获得最大纯利润,约为4.1万元.
方法归纳
二次函数模型主要用来解决实际问题中的利润最大、用料最省等问题,是高考考查的重点.解题时,建立二次函数解析式后,可以利用配方法、判别式法、换元法、函数的单调性等来求函数的最值,从而解决实际问题.
3.某汽车租赁公司拥有汽车100辆.每辆车的月租金为3000元时,可全部租出,每辆车的月租金每增加50元,未租出的车就会增加一辆租出的车每辆每月需要维护费150元,未租出的车每辆每月要维护费50 元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
解析
(1)当每辆车的月租金定为3600元时,未租出的车辆数为,所以这时租出了辆车.
(2)设每辆车的月租金定为元,租赁公司的月收益为元,
则
所以
所以,当时,最大,其最大值为307050.
因此当每辆车的月租金定为4050元时,租赁公司的月收益最大,最大月收益为307050元.
变式训练
典例讲解
例4、某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元.
(1)分别写出两类产品的收益与投资额的函数关系式;
(2)该家庭现有20万元资金,全部用于理财投资,怎么分配资金能使投资获得最大收益?最大收益是多少万元?
解析
(1)设两类产品的收益与投资额的函数关系式分别为:
,从而有,
所以.
典例讲解
例4、某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元.
(1)分别写出两类产品的收益与投资额的函数关系式;
(2)该家庭现有20万元资金,全部用于理财投资,怎么分配资金能使投资获得最大收益?最大收益是多少万元?
解析
(2)设投资债券产品万元,则股票类投资为万元,获得的收益为万元.
令,则,
所以当,即时,取得最大值, .所以当投资债券16万元,投资股票4万元时,能获得最大收益,最大收益是3万元.
方法归纳
(1)给出含参数的函数关系式,利用待定系数法求出参数,确定函数关系式.
(2)根据题意,直接列出相应的函数关系式.
幂函数模型应用的求解策略
变式训练
4.在固定压力差(压力差为常数)下,当气体通过圆形管道时,其流量速度与管道半径的四次方成正比.
(1)若气体在半径为的管道中,流量速度为400,求该气体通过半径为r的管道时,其流量速度的函数解析式;
(2)已知(1)中的气体通过的管道半径为,计算该气体的流量速度(保留一位小数).
(1)设.
因为当时,,所以,故所求函数解析式为.
(2)当时,该气体的流量速度为.
解析
当堂练习
1.某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,开源节流,现要从这些边角料上截取矩形铁片(如图中阴影部分)备用,当截取的矩形面积最大时,矩形两边长应为( )
A. B. C. D.
A
当堂练习
2.加工爆米花时,爆开且不娴的粒数占加工总粒数的百分比称为“可食用率”.在特定条件下,可食用率与加工时间(单位:分钟)满足函数关系是常数),如图记录了三次试验的数据.根据上述函数模型和试验数据,可以得到最佳加工时间为( )
A.分钟 B. 分钟 C. D.
B
当堂练习
3.国家规定个人稿费的纳税办法是:不超过800元的不纳税;超过800而不超过4000元的按超过800元部分的14%纳税;超过4000元的按全部稿酬的11%纳税,某人出版了一本书,共纳税420元,则这个人的稿费为 元.
4.现测得的两组对应值分别为(1,2),(2,5),现有两个待选模型,甲:,乙:,若又测得的一组对应值为(3,10.2),则应选用 作为函数模型.
3800
甲
归纳小结
作 业
教材P95练习:1、3
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
