高中数学必修第一册人教A版(2019)3.4《函数的应用(一)》真题探源课件(共15张PPT)
文档属性
| 名称 | 高中数学必修第一册人教A版(2019)3.4《函数的应用(一)》真题探源课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 43.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-03 10:25:25 | ||
图片预览






文档简介
(共15张PPT)
《函数的应用(一)》真题探源
高考对函数模型应用的考查主要是二次函数、分段函数模型的建立及最值的求解,分段函数涉及二次函数、反比例函数、幂函数、对勾函数等.题型以图表型的填空题、选择题为主,但部分试题中也有以解答题形式出现的.
考情揭秘
题型1、图表型的应用问题
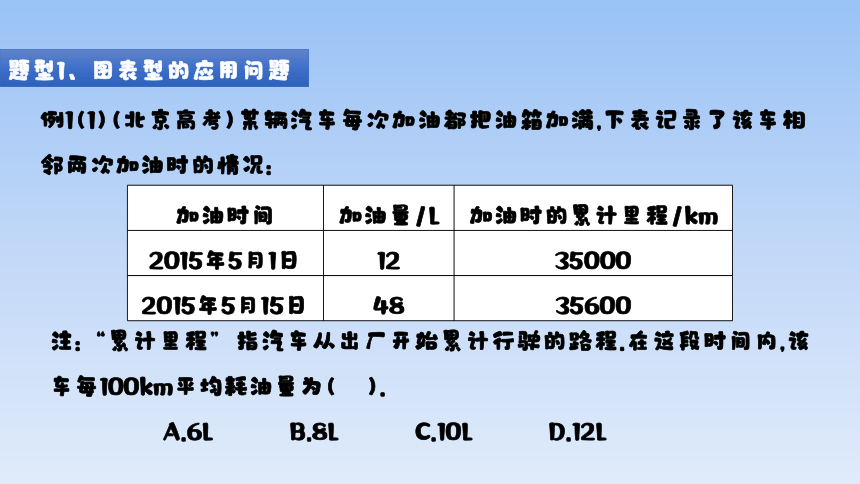
例1(1)(北京高考)某辆汽车每次加油都把油箱加满,下表记录了该车相邻两次加油时的情况:
注:“累计里程”指汽车从出厂开始累计行驶的路程.在这段时间内,该车每100km平均耗油量为( ).
A.6L B.8L C.10L D.12L
加油时间 加油量/L 加油时的累计里程/km
2015年5月1日 12 35000
2015年5月15日 48 35600
(2)(2018·全国|高考)某地区经过一年的新农村建设,农村的经济收入增加了一倍.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设后农村的经济收入构成比例,得到如下扇形分布图:
题型1、图表型的应用问题
则下面结论中不正确的是( ).
A.新农村建设后种植收入减少
B.新农村建设后,其他收入增加了一倍以上
C.新农村建设后,养殖收入增加一倍
D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
真题溯源
本题取材于教材P94例2、P96习题34第4题.主要考查函数图像的实际应用等基本知识,以及数形结合等基本思想.考查直观想象、数学建模等学科核心素养.
思路点拨
(1)因为第一次(即5月1日)把油加满,而第二次把油加满加了48L,即汽车行驶35600-35000=600(km)耗油48L,所以每100km的耗油量为8L.故选B.
题型1、图表型的应用问题
思路点拨
(2)种植收入60%·a变为37%·2a,增加了,而不是减少,故A不正确;其他收入4%·a变为5%·2a,增加了一倍以上,B正确;养殖收入由30%·a变为30%×2a,增加了一倍,C正确;养殖收入与第三产业收入为总收入的30%+28%=58%>50%,D也正确.故选A.
答 (1)B (2)A
题型1、图表型的应用问题
例2(1)(北京高考)加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比被称为“可食用率”.在特定条件下,可食用率p与加工时间(单位:min)满足函数关系(a,b,c是常数),如图记录了三次实验的数据.根据上述函数模型和实验数据,可以得到最佳加工时间为( ).
A.3.50min B.3.75min
C.4.00min D.4.25min
题型2、二次函数模型的实际应用题
(2)(2018·河北衡水二中月考)某工厂生产的A种产品进入某商场销售,商场为吸引厂家第一年免收管理费,因此第一年A种产品定价为每件70元,年销售量为11.8万件,从第二年开始,商场对A种产品征收销售额的x%的管理费(即销售100元要征收x元),于是该产品定价每件比第年增加了元,预计年销售量减少x万件,要使第二年商场在A种产品经营中收取的管理费不少于14万元,则x的最大值是( ).
A.2 B.6.5 C.8.8 D.10
题型2、二次函数模型的实际应用题
真题溯源
二次函数是我们最熟悉的函数之一,在初中我们就对二次函数有过研究,教材P95练习第1题和第3题及P95习题3.4的第1题都是二次函数的应用.
(1)由实验数据和函数模型知,二次函数的图像过点(3,0.7),
题型2、二次函数模型的实际应用题
思路点拨
(4,0.8),(5,0.5),分别代入解析式,得,解得,所以,所以当t=3.75时,可食用率p最大.故选B.
题型2、二次函数模型的实际应用题
思路点拨
(2)由已知有第二年的年销售收入为万元,商场对该商品征收的管理费记为y万元,,所以,化简得,故x的最大值为10,选D.
答 (1)B (2)D
题型3、分段函数模型的应用
例3(2018·黄冈上学期第一次调考)提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v(单位:km/h)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60km/h.研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤200时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/时)可以达到最大,并求出最大值.(精确到1辆/时)
分段函数是刻画现实问题的重要模型,现实生活中有很多问题都是用分段函数表示的,如出租车计费、个人所得税等.这类题型教材中到处可见,如P93例1,P94例2以及P96习题3.4第3题都是分段函数模型的应用.这类问题考查数学建模和数学运算的学科核心素养.
题型3、分段函数模型的应用
真题溯源
(1)由题意,当0≤x≤20时,v(x)=60,当20≤x≤200时,设v(x)=ax+b.由已知得,解.故函数v(x)的表达式为.
思路点拨
题型3、分段函数模型的应用
依题意并结合(1)可得.当0≤x≤20,为增函数,故当x=20时在区间[0,20]上取得最大值60×20=1200;当20≤x≤200时,.当且仅当x=100时,等号成立.所以当x=100时, 在区间[20,200]上取得最大值.综上可得,当x=100时,在区间[0,200]上取得最大值≈3333,即当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3333辆/时.
思路点拨
题型3、分段函数模型的应用
(1)求分段函数的最值,先求函数在每一段范围内的最值,然后比较这几个最值的大小,最后求出分段函数的最值.
(2)分段函数主要是每一段自变量变化所遵循的规律不同,可以先将其看成几个问题,将各段的变化规律分别找出来,再将其合到一起,要注意各段自变量的范围,特别是端点值.
解题通法
分段函数模型的解题策略
《函数的应用(一)》真题探源
高考对函数模型应用的考查主要是二次函数、分段函数模型的建立及最值的求解,分段函数涉及二次函数、反比例函数、幂函数、对勾函数等.题型以图表型的填空题、选择题为主,但部分试题中也有以解答题形式出现的.
考情揭秘
题型1、图表型的应用问题
例1(1)(北京高考)某辆汽车每次加油都把油箱加满,下表记录了该车相邻两次加油时的情况:
注:“累计里程”指汽车从出厂开始累计行驶的路程.在这段时间内,该车每100km平均耗油量为( ).
A.6L B.8L C.10L D.12L
加油时间 加油量/L 加油时的累计里程/km
2015年5月1日 12 35000
2015年5月15日 48 35600
(2)(2018·全国|高考)某地区经过一年的新农村建设,农村的经济收入增加了一倍.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设后农村的经济收入构成比例,得到如下扇形分布图:
题型1、图表型的应用问题
则下面结论中不正确的是( ).
A.新农村建设后种植收入减少
B.新农村建设后,其他收入增加了一倍以上
C.新农村建设后,养殖收入增加一倍
D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
真题溯源
本题取材于教材P94例2、P96习题34第4题.主要考查函数图像的实际应用等基本知识,以及数形结合等基本思想.考查直观想象、数学建模等学科核心素养.
思路点拨
(1)因为第一次(即5月1日)把油加满,而第二次把油加满加了48L,即汽车行驶35600-35000=600(km)耗油48L,所以每100km的耗油量为8L.故选B.
题型1、图表型的应用问题
思路点拨
(2)种植收入60%·a变为37%·2a,增加了,而不是减少,故A不正确;其他收入4%·a变为5%·2a,增加了一倍以上,B正确;养殖收入由30%·a变为30%×2a,增加了一倍,C正确;养殖收入与第三产业收入为总收入的30%+28%=58%>50%,D也正确.故选A.
答 (1)B (2)A
题型1、图表型的应用问题
例2(1)(北京高考)加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比被称为“可食用率”.在特定条件下,可食用率p与加工时间(单位:min)满足函数关系(a,b,c是常数),如图记录了三次实验的数据.根据上述函数模型和实验数据,可以得到最佳加工时间为( ).
A.3.50min B.3.75min
C.4.00min D.4.25min
题型2、二次函数模型的实际应用题
(2)(2018·河北衡水二中月考)某工厂生产的A种产品进入某商场销售,商场为吸引厂家第一年免收管理费,因此第一年A种产品定价为每件70元,年销售量为11.8万件,从第二年开始,商场对A种产品征收销售额的x%的管理费(即销售100元要征收x元),于是该产品定价每件比第年增加了元,预计年销售量减少x万件,要使第二年商场在A种产品经营中收取的管理费不少于14万元,则x的最大值是( ).
A.2 B.6.5 C.8.8 D.10
题型2、二次函数模型的实际应用题
真题溯源
二次函数是我们最熟悉的函数之一,在初中我们就对二次函数有过研究,教材P95练习第1题和第3题及P95习题3.4的第1题都是二次函数的应用.
(1)由实验数据和函数模型知,二次函数的图像过点(3,0.7),
题型2、二次函数模型的实际应用题
思路点拨
(4,0.8),(5,0.5),分别代入解析式,得,解得,所以,所以当t=3.75时,可食用率p最大.故选B.
题型2、二次函数模型的实际应用题
思路点拨
(2)由已知有第二年的年销售收入为万元,商场对该商品征收的管理费记为y万元,,所以,化简得,故x的最大值为10,选D.
答 (1)B (2)D
题型3、分段函数模型的应用
例3(2018·黄冈上学期第一次调考)提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v(单位:km/h)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60km/h.研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤200时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/时)可以达到最大,并求出最大值.(精确到1辆/时)
分段函数是刻画现实问题的重要模型,现实生活中有很多问题都是用分段函数表示的,如出租车计费、个人所得税等.这类题型教材中到处可见,如P93例1,P94例2以及P96习题3.4第3题都是分段函数模型的应用.这类问题考查数学建模和数学运算的学科核心素养.
题型3、分段函数模型的应用
真题溯源
(1)由题意,当0≤x≤20时,v(x)=60,当20≤x≤200时,设v(x)=ax+b.由已知得,解.故函数v(x)的表达式为.
思路点拨
题型3、分段函数模型的应用
依题意并结合(1)可得.当0≤x≤20,为增函数,故当x=20时在区间[0,20]上取得最大值60×20=1200;当20≤x≤200时,.当且仅当x=100时,等号成立.所以当x=100时, 在区间[20,200]上取得最大值.综上可得,当x=100时,在区间[0,200]上取得最大值≈3333,即当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3333辆/时.
思路点拨
题型3、分段函数模型的应用
(1)求分段函数的最值,先求函数在每一段范围内的最值,然后比较这几个最值的大小,最后求出分段函数的最值.
(2)分段函数主要是每一段自变量变化所遵循的规律不同,可以先将其看成几个问题,将各段的变化规律分别找出来,再将其合到一起,要注意各段自变量的范围,特别是端点值.
解题通法
分段函数模型的解题策略
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
