1.1.1任意角(第二课时)
图片预览





文档简介
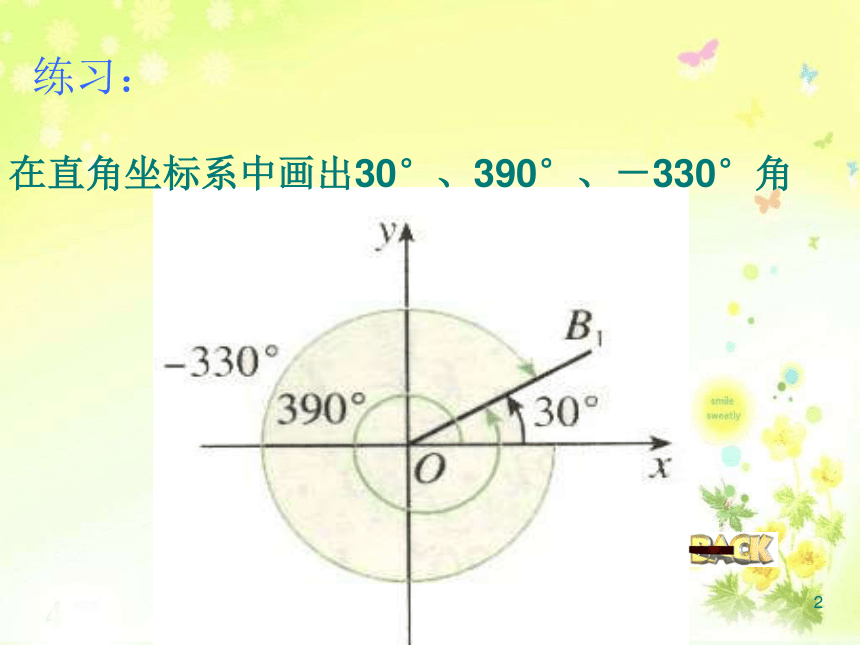
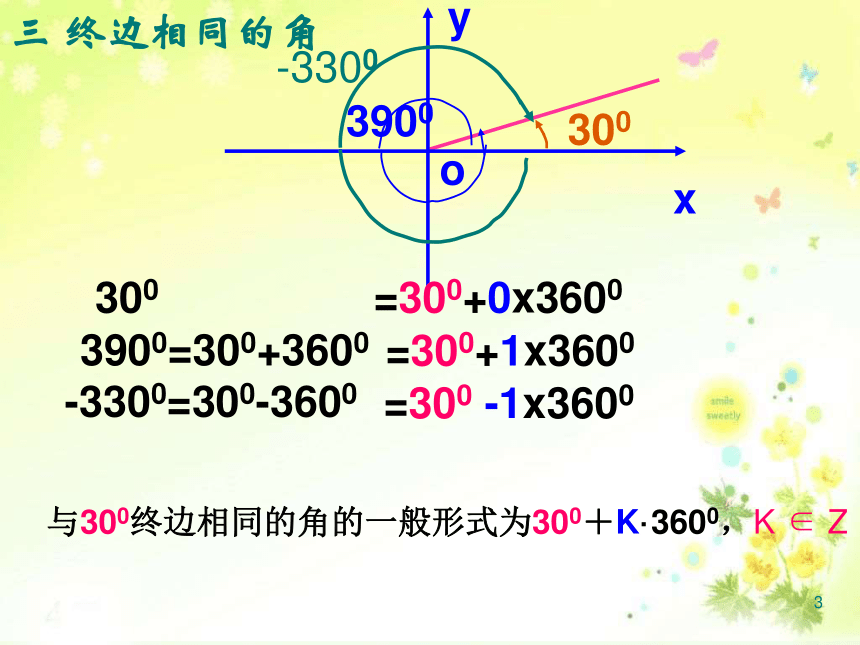
课件16张PPT。11.1.1 任意角2在直角坐标系中画出30°、390°、-330°角练习:33900-33003900=300+3600-3300=300-3600=300+1x3600 =300 -1x3600 300 =300+0x3600与300终边相同的角的一般形式为300+K·3600,K ∈ Z三 终边相同的角4注:(1) k ∈ Z (4)终边相同的角不一定相等,但相等的角终边一定相同,终边相同的角有无数多个,它们相差360°的整数倍。与 终边相同的角的集合为(2) 是任意角(3)K·360°与 之间是“+”号,
5例1、在0°到360°范围内,找出与下列各角终边相同的角,并判断它是哪个象限的角?(1)-120°(2)640 °(3) -950 ° 12'解(1)-120°= -360 °+240 °
所以与-120 °角终边相同的角是240 °角,它是第三象限角。 6(2)640°=360°+280°
所以与640°角终边相同的角是280°角,它是第四象限角。 (3)-950°12’ = -3×360°+129°48'
所以与-950°12’ 角终边相同的角是129°48 ’ 角,它是第二象限角。 7判断角 α 是第几象限角的方法:
选取适当的整数k,使得β=α+k*3600(其中00≤β<3600 ),那么β是第几象限角,则α是第几象限角。8写出终边落在x轴正半轴y轴正半轴x轴负半轴y轴负半轴的角的集合。0090018002700 +Kx3600+Kx3600+Kx3600+Kx3600或3600+KX36009象限角的表示法记!!102、写出下列各角终边相同的角的集合,并把集合中适合不等式 的元素 写出来。
(1) 60° (3)-225°解:与终边相同的角的集合为S中适合 的元素是60°, -300°, -660°11例3 写出终边落在y轴上的角的集合。解:终边落在y轴正半轴上的角的集合为S1={β| β=900+K?3600,K∈Z} ={β| β=900+2K?1800,K∈Z}终边落在y轴负半轴上的角的集合为S2={β| β=2700+K?3600,K∈Z}={β| β=900+1800+2K?1800,K∈Z}={β| β=900+(2K+1)1800 ,K∈Z}12S=S1∪S2所以 终边落在y轴上的角的集合为={β| β=900+1800 的偶数倍}∪{β| β=900+1800 的奇数倍}={β| β=900+1800 的整数倍} ={β| β=900+n?1800 ,n∈Z}13合作探究终边落在X轴的正半轴的集合:S={β/ β =0o+K·360o,K∈Z};终边落在X轴的负半轴的集合:S={β/ β =180o+K·360o,K∈Z};终边落在Y轴的正半轴的集合:S={β/ β =90o+K·360o,K∈Z};终边落在Y轴的负半轴的集合:S={β/ β =270o+K·360o,K∈Z};终边落在X轴上的集合:S={β/ β =0o+K·180o,K∈Z};终边落在Y轴上的集合:S={β/ β =90o+K·180o,K∈Z};终边落在坐标轴上的集合:S={β/ β =0o+K·90o,K∈Z};14例2:写出终边在函数y=x的图象上的角的集合S. 【分析】函数y=x的图象是一条直线(一、三象限的角平分线),而角的终边是一条射线,故应分别求出终边在一、三象限的角,再求其并集.15 【解析】在0°到360°的范围内,终边在函数y=x的图象上的角有两个,即45°和225°.
因此,所有与45°角终边相同的角构成集合:
S1={β|β=45°+k·360°,k∈Z}
={β|β=45°+2k·180°,k∈Z},
而所有与225°角终边相同的角构成集合:
S2={β|β=225°+k·360°,k∈Z}
={β|β=45°+(2k+1)·180°,k∈Z},
于是,终边在函数y=x图象如图上的角的集合:
S=S1∪S2
={β|β=45°+2k·180°,k∈Z}∪{β|β=45°+
(2k+1)·180°,k∈Z} ={β|β=45°+n·180°,n∈Z}.16小结:1.任意角
的概念正角:射线按逆时针方向旋转形成的角负角:射线按顺时针方向旋转形成的角零角:射线不作旋转形成的角1)置角的顶点于原点2)始边重合于X轴的非负半轴2.象限角终边落在第几象限就是第几象限角3 . 终边与 角a相同的角
5例1、在0°到360°范围内,找出与下列各角终边相同的角,并判断它是哪个象限的角?(1)-120°(2)640 °(3) -950 ° 12'解(1)-120°= -360 °+240 °
所以与-120 °角终边相同的角是240 °角,它是第三象限角。 6(2)640°=360°+280°
所以与640°角终边相同的角是280°角,它是第四象限角。 (3)-950°12’ = -3×360°+129°48'
所以与-950°12’ 角终边相同的角是129°48 ’ 角,它是第二象限角。 7判断角 α 是第几象限角的方法:
选取适当的整数k,使得β=α+k*3600(其中00≤β<3600 ),那么β是第几象限角,则α是第几象限角。8写出终边落在x轴正半轴y轴正半轴x轴负半轴y轴负半轴的角的集合。0090018002700 +Kx3600+Kx3600+Kx3600+Kx3600或3600+KX36009象限角的表示法记!!102、写出下列各角终边相同的角的集合,并把集合中适合不等式 的元素 写出来。
(1) 60° (3)-225°解:与终边相同的角的集合为S中适合 的元素是60°, -300°, -660°11例3 写出终边落在y轴上的角的集合。解:终边落在y轴正半轴上的角的集合为S1={β| β=900+K?3600,K∈Z} ={β| β=900+2K?1800,K∈Z}终边落在y轴负半轴上的角的集合为S2={β| β=2700+K?3600,K∈Z}={β| β=900+1800+2K?1800,K∈Z}={β| β=900+(2K+1)1800 ,K∈Z}12S=S1∪S2所以 终边落在y轴上的角的集合为={β| β=900+1800 的偶数倍}∪{β| β=900+1800 的奇数倍}={β| β=900+1800 的整数倍} ={β| β=900+n?1800 ,n∈Z}13合作探究终边落在X轴的正半轴的集合:S={β/ β =0o+K·360o,K∈Z};终边落在X轴的负半轴的集合:S={β/ β =180o+K·360o,K∈Z};终边落在Y轴的正半轴的集合:S={β/ β =90o+K·360o,K∈Z};终边落在Y轴的负半轴的集合:S={β/ β =270o+K·360o,K∈Z};终边落在X轴上的集合:S={β/ β =0o+K·180o,K∈Z};终边落在Y轴上的集合:S={β/ β =90o+K·180o,K∈Z};终边落在坐标轴上的集合:S={β/ β =0o+K·90o,K∈Z};14例2:写出终边在函数y=x的图象上的角的集合S. 【分析】函数y=x的图象是一条直线(一、三象限的角平分线),而角的终边是一条射线,故应分别求出终边在一、三象限的角,再求其并集.15 【解析】在0°到360°的范围内,终边在函数y=x的图象上的角有两个,即45°和225°.
因此,所有与45°角终边相同的角构成集合:
S1={β|β=45°+k·360°,k∈Z}
={β|β=45°+2k·180°,k∈Z},
而所有与225°角终边相同的角构成集合:
S2={β|β=225°+k·360°,k∈Z}
={β|β=45°+(2k+1)·180°,k∈Z},
于是,终边在函数y=x图象如图上的角的集合:
S=S1∪S2
={β|β=45°+2k·180°,k∈Z}∪{β|β=45°+
(2k+1)·180°,k∈Z} ={β|β=45°+n·180°,n∈Z}.16小结:1.任意角
的概念正角:射线按逆时针方向旋转形成的角负角:射线按顺时针方向旋转形成的角零角:射线不作旋转形成的角1)置角的顶点于原点2)始边重合于X轴的非负半轴2.象限角终边落在第几象限就是第几象限角3 . 终边与 角a相同的角
