【新课标】4.8.1图形的位似 课件(共23张PPT)
文档属性
| 名称 | 【新课标】4.8.1图形的位似 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-03 10:37:11 | ||
图片预览




文档简介
(共23张PPT)
4.8.1图形的位似
北师版九年级上册
教学目标
1、了解位似图形、位似中心的概念,掌握位似图形的性质。
2、掌握位似图形的画法,能够利用位似图形的性质将图形放大或缩小。
情境导入
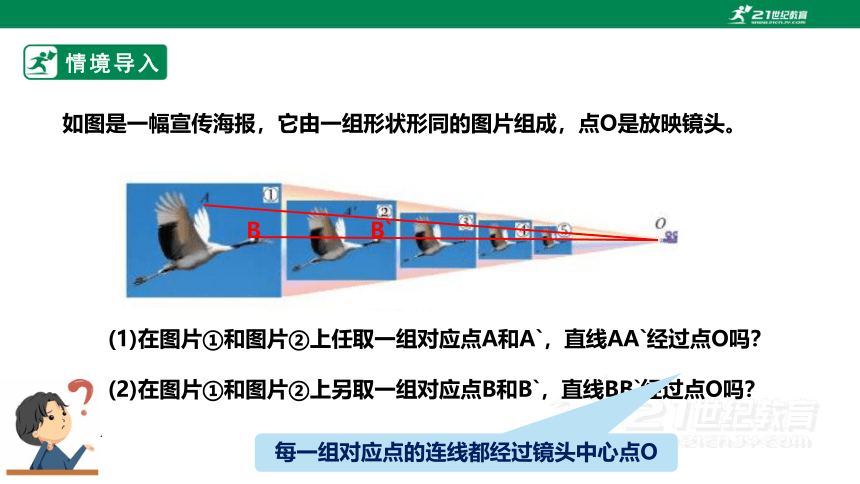
如图是一幅宣传海报,它由一组形状形同的图片组成,点O是放映镜头。
(1)在图片①和图片②上任取一组对应点A和A`,直线AA`经过点O吗?
(2)在图片①和图片②上另取一组对应点B和B`,直线BB`经过点O吗?
B
B`
每一组对应点的连线都经过镜头中心点O
新知讲解
A
B
C
D
E
E'
D'
C'
B'
A'
O
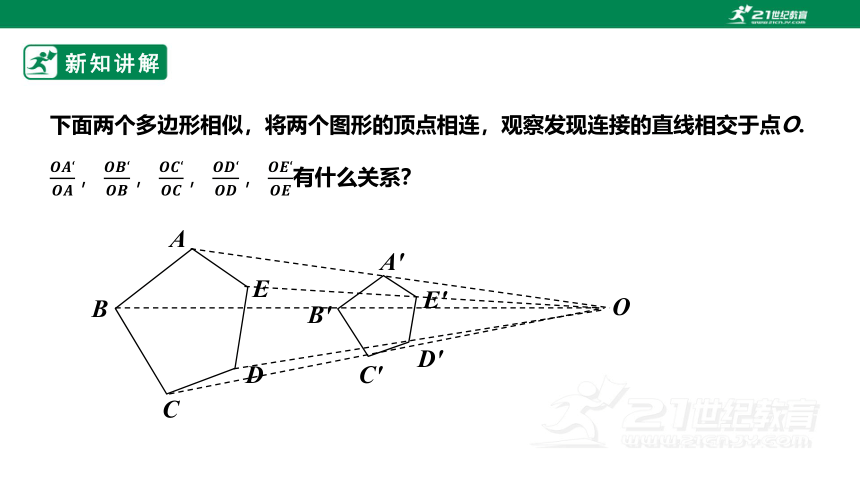
下面两个多边形相似,将两个图形的顶点相连,观察发现连接的直线相交于点O. 有什么关系?
归纳总结
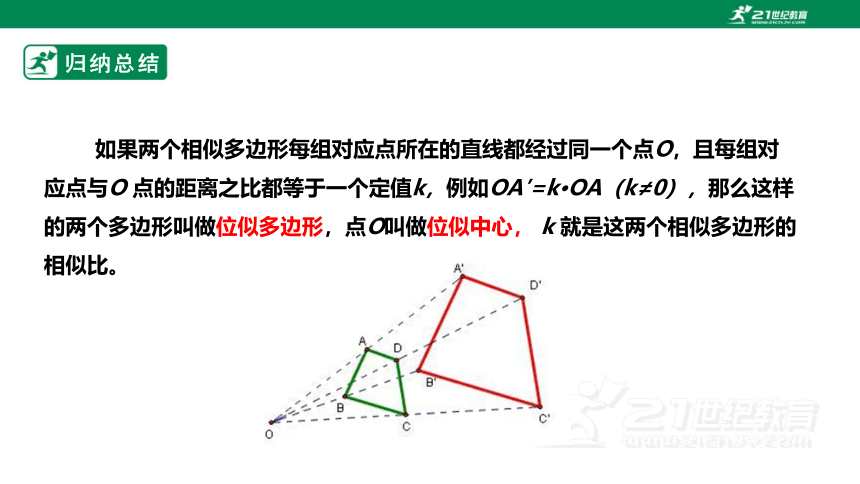
如果两个相似多边形每组对应点所在的直线都经过同一个点O,且每组对应点与O 点的距离之比都等于一个定值k,例如OA′=k·OA(k≠0),那么这样的两个多边形叫做位似多边形,点O叫做位似中心, k 就是这两个相似多边形的相似比。
归纳总结
1.两个多边形是位似多边形应满足两个条件:
①是相似多边形;②每组对应点所在直线都经过同一个点。这两个条件缺一不可。
2.两个位似图形的位似中心有且只有一个。
3.位似多边形是相似多边形,但相似多边形不一定是位似多边形。
新知讲解
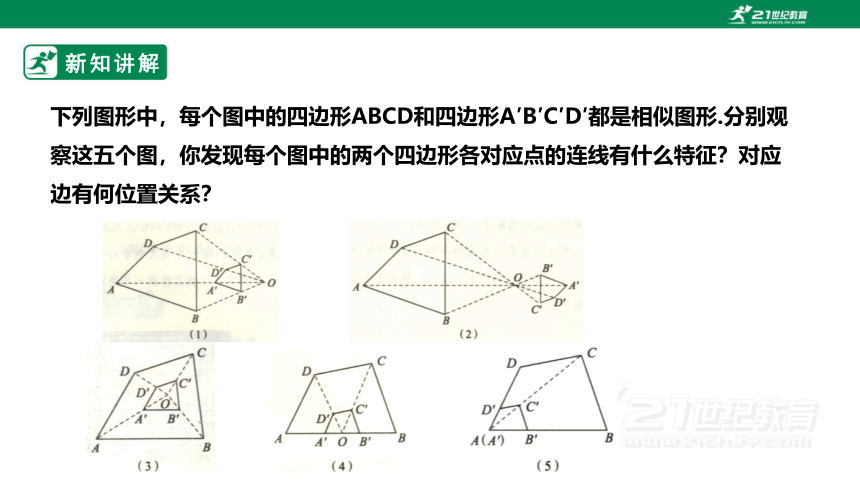
下列图形中,每个图中的四边形ABCD和四边形A′B′C′D′都是相似图形.分别观察这五个图,你发现每个图中的两个四边形各对应点的连线有什么特征?对应边有何位置关系?
归纳总结
位似图形的性质
1.位似图形上任意一对对应点到位似中心的距离之比等于相似比;
2.位似图形上的每组对应点和位似中心在同一条直线上;
3.位似图形的对应线段平行或在同一条直线上;
4.位似图形是特殊的相似图形,因此位似图形具有相似图形的一切性质。
典例精析
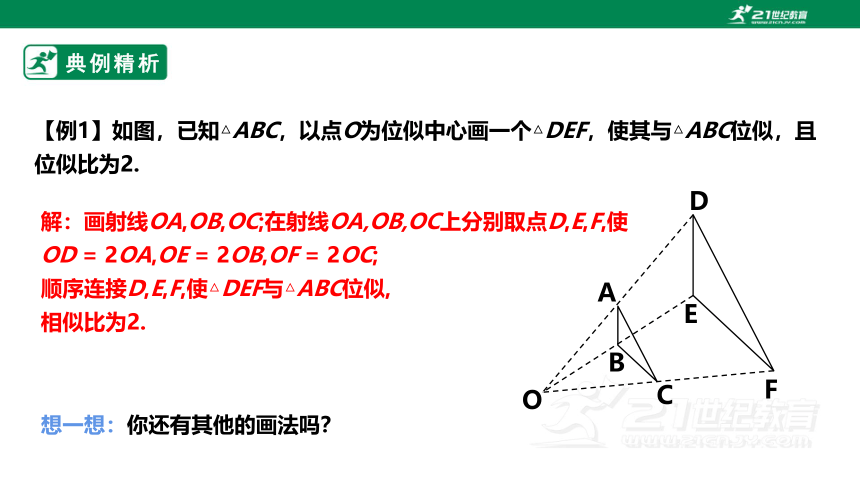
【例1】如图,已知△ABC,以点O为位似中心画一个△DEF,使其与△ABC位似,且位似比为2.
解:画射线OA,OB,OC;在射线OA,OB,OC上分别取点D,E,F,使
OD = 2OA,OE = 2OB,OF = 2OC;
顺序连接D,E,F,使△DEF与△ABC位似,
相似比为2.
想一想:你还有其他的画法吗?
A
B
C
F
E
D
O
典例精析
A
B
C
画法二:△ABC与△DEF异侧.
解:画射线OA、OB、OC;沿着射线OA、OB、OC反方向上分别取点D、E、F,OD = 2OA,OE = 2OB,OF = 2OC;顺次连结D、E、F,使△DEF与△ABC位似,相似比为2.
O
E
F
D
归纳总结
画位似的一般步骤:
① 确定位似中心;
② 分别连接并延长位似中心和能代表原图的关键点;
③ 根据相似比,确定能代表所作的位似图形的关键点;
④ 顺次连接上述各点,得到放大或缩小的图形.
做一做
用以下方法可以近似地把一个不规则图形放大:
1.将两根等长的橡皮筋系在一起,联结处形成一个结点。
2.选一个图形,再选一个定点,将橡皮筋的一端固定在定点处,把铅笔固定在另一端。
利用位似可以把一个图形放大或缩小
3.拉动铅笔,使结点沿图形的边缘移动一周,这样铅笔就画出一个新的图形。试试看,它们相似吗?
课堂练习
1.如图,△A1B1C1与△ABC是位似图形,且面积比为4∶9,则下列结论错误的是( )
A.点O为位似中心,位似比为2∶3
B.A1B1∥AB,A1B1∶AB=2∶3
C.△A1B1C1与△ABC的周长比为2∶3
D.OA1∶A1A=2∶3
D
课堂练习
2. 如图,正五边形 FGHMN 与正五边形 ABCDE 是位似图形,若AB : FG = 3 :5,则下列结论正确的是( )
A. 3 DE = 5MN B. 5DE = 3 MN
C. 3∠A = 5∠F D. 5∠A = 3∠F
B
A
B
E
C
D
N
F
G
H
M
课堂练习
3.如图,火焰的光线穿过小孔O,在竖直的屏幕上形成倒立的实像,像的长度BD=2 cm,OA=60 cm,OB=15 cm,则AC的长度为_________.
8 cm
课堂练习
4.如图,△ABC与△A′B′C′是位似图形,且位似比是1∶2,若AB=2 cm,则A′B′=___ cm.
(1)请在图中画出位似中心O;
(2)AC∶A′C′=________;
(3)AB与A′B′的位置关系为________.
4
1:2
平行
A
C
B
A′
B′
C′
O
课堂练习
5.如图,△ABC与△A′B′C′关于点O位似,BO=3,B′O=6.
(1)若AC=5,求A′C′的长;(2)若△ABC的面积为7,求△A′B′C′的面积.
A
B
C
O
A′
B′
C′
课堂练习
解:(1)∵△ABC与△A′B′C′是位似图形,
位似比为OB∶OB′=3∶6=1∶2,
∴ =,即=,
∴A′C′=10;
(2)根据题意,得=()2=,
即=,
∴S△A′B′C′=7×4=28.
A
B
C
O
A′
B′
C′
课堂总结
如果两个图形不仅形状相同,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形.
这个点叫做位似中心.
这时的相似比又称为位似比.
位似图形的概念
位似图形的性质
1.位似图形上任意一对对应点到位似中心的距离之比等于相似比;
2.位似图形上的每组对应点和位似中心在同一条直线上;
3.位似图形的对应线段平行或在同一条直线上;
4.位似图形是特殊的相似图形,因此位似图形具有相似图形的一切
性质。
板书设计
4.8.1位似图形
1、位似图形
2、性质
作业布置
教材第115页习题4.13 1,2题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
4.8.1图形的位似
北师版九年级上册
教学目标
1、了解位似图形、位似中心的概念,掌握位似图形的性质。
2、掌握位似图形的画法,能够利用位似图形的性质将图形放大或缩小。
情境导入
如图是一幅宣传海报,它由一组形状形同的图片组成,点O是放映镜头。
(1)在图片①和图片②上任取一组对应点A和A`,直线AA`经过点O吗?
(2)在图片①和图片②上另取一组对应点B和B`,直线BB`经过点O吗?
B
B`
每一组对应点的连线都经过镜头中心点O
新知讲解
A
B
C
D
E
E'
D'
C'
B'
A'
O
下面两个多边形相似,将两个图形的顶点相连,观察发现连接的直线相交于点O. 有什么关系?
归纳总结
如果两个相似多边形每组对应点所在的直线都经过同一个点O,且每组对应点与O 点的距离之比都等于一个定值k,例如OA′=k·OA(k≠0),那么这样的两个多边形叫做位似多边形,点O叫做位似中心, k 就是这两个相似多边形的相似比。
归纳总结
1.两个多边形是位似多边形应满足两个条件:
①是相似多边形;②每组对应点所在直线都经过同一个点。这两个条件缺一不可。
2.两个位似图形的位似中心有且只有一个。
3.位似多边形是相似多边形,但相似多边形不一定是位似多边形。
新知讲解
下列图形中,每个图中的四边形ABCD和四边形A′B′C′D′都是相似图形.分别观察这五个图,你发现每个图中的两个四边形各对应点的连线有什么特征?对应边有何位置关系?
归纳总结
位似图形的性质
1.位似图形上任意一对对应点到位似中心的距离之比等于相似比;
2.位似图形上的每组对应点和位似中心在同一条直线上;
3.位似图形的对应线段平行或在同一条直线上;
4.位似图形是特殊的相似图形,因此位似图形具有相似图形的一切性质。
典例精析
【例1】如图,已知△ABC,以点O为位似中心画一个△DEF,使其与△ABC位似,且位似比为2.
解:画射线OA,OB,OC;在射线OA,OB,OC上分别取点D,E,F,使
OD = 2OA,OE = 2OB,OF = 2OC;
顺序连接D,E,F,使△DEF与△ABC位似,
相似比为2.
想一想:你还有其他的画法吗?
A
B
C
F
E
D
O
典例精析
A
B
C
画法二:△ABC与△DEF异侧.
解:画射线OA、OB、OC;沿着射线OA、OB、OC反方向上分别取点D、E、F,OD = 2OA,OE = 2OB,OF = 2OC;顺次连结D、E、F,使△DEF与△ABC位似,相似比为2.
O
E
F
D
归纳总结
画位似的一般步骤:
① 确定位似中心;
② 分别连接并延长位似中心和能代表原图的关键点;
③ 根据相似比,确定能代表所作的位似图形的关键点;
④ 顺次连接上述各点,得到放大或缩小的图形.
做一做
用以下方法可以近似地把一个不规则图形放大:
1.将两根等长的橡皮筋系在一起,联结处形成一个结点。
2.选一个图形,再选一个定点,将橡皮筋的一端固定在定点处,把铅笔固定在另一端。
利用位似可以把一个图形放大或缩小
3.拉动铅笔,使结点沿图形的边缘移动一周,这样铅笔就画出一个新的图形。试试看,它们相似吗?
课堂练习
1.如图,△A1B1C1与△ABC是位似图形,且面积比为4∶9,则下列结论错误的是( )
A.点O为位似中心,位似比为2∶3
B.A1B1∥AB,A1B1∶AB=2∶3
C.△A1B1C1与△ABC的周长比为2∶3
D.OA1∶A1A=2∶3
D
课堂练习
2. 如图,正五边形 FGHMN 与正五边形 ABCDE 是位似图形,若AB : FG = 3 :5,则下列结论正确的是( )
A. 3 DE = 5MN B. 5DE = 3 MN
C. 3∠A = 5∠F D. 5∠A = 3∠F
B
A
B
E
C
D
N
F
G
H
M
课堂练习
3.如图,火焰的光线穿过小孔O,在竖直的屏幕上形成倒立的实像,像的长度BD=2 cm,OA=60 cm,OB=15 cm,则AC的长度为_________.
8 cm
课堂练习
4.如图,△ABC与△A′B′C′是位似图形,且位似比是1∶2,若AB=2 cm,则A′B′=___ cm.
(1)请在图中画出位似中心O;
(2)AC∶A′C′=________;
(3)AB与A′B′的位置关系为________.
4
1:2
平行
A
C
B
A′
B′
C′
O
课堂练习
5.如图,△ABC与△A′B′C′关于点O位似,BO=3,B′O=6.
(1)若AC=5,求A′C′的长;(2)若△ABC的面积为7,求△A′B′C′的面积.
A
B
C
O
A′
B′
C′
课堂练习
解:(1)∵△ABC与△A′B′C′是位似图形,
位似比为OB∶OB′=3∶6=1∶2,
∴ =,即=,
∴A′C′=10;
(2)根据题意,得=()2=,
即=,
∴S△A′B′C′=7×4=28.
A
B
C
O
A′
B′
C′
课堂总结
如果两个图形不仅形状相同,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形.
这个点叫做位似中心.
这时的相似比又称为位似比.
位似图形的概念
位似图形的性质
1.位似图形上任意一对对应点到位似中心的距离之比等于相似比;
2.位似图形上的每组对应点和位似中心在同一条直线上;
3.位似图形的对应线段平行或在同一条直线上;
4.位似图形是特殊的相似图形,因此位似图形具有相似图形的一切
性质。
板书设计
4.8.1位似图形
1、位似图形
2、性质
作业布置
教材第115页习题4.13 1,2题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
