15.2.2分式的混合运算 课件(共27张PPT)
文档属性
| 名称 | 15.2.2分式的混合运算 课件(共27张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-04 12:28:25 | ||
图片预览








文档简介
(共27张PPT)
15.2.2 分式的混合运算
人教版八年级上册
知识回顾
分式的加减法法则
同分母分式相加减,分母不变,把分子相加减.
用式子表示:
异分母分式相加减,先通分,变为同分母的分式,再加减.
知识回顾
分式的乘除、乘方混合运算:
分式的乘除、乘方混合运算顺序与分数的乘除、乘方混合运算顺序相同,即先乘方,再乘除,有括号的先算括号里面的.
教学目标
1.掌握分式的混合运算法则和计算步骤.
2.能熟练运用分式的混合运算法则进行计算.
新知导入
同样,我们先类比有理数的混合运算,有理数的混合运算法则是什么?
1.先算乘方,再算乘除,最后算加减;
2.同级运算,按照从左至右的顺序进行;
3.如果有括号,就先算小括号里的,再算中括号里的,然后算大括号里的.
新知探究
知识点 1
分式的混合运算
分式的混合运算
先算乘方,再算乘除,最后算加减;若有括号,则先算括号里面的;同级运算,按从左到右的顺序进行计算.
结合我们已经学习的分式乘除、乘方混合运算法则,可以得出:
新知典例
例1 计算:
解:原式
注意:①要先观察算式,可以看到此题,除平方外,没有其他括号存在,所以先乘方,再乘除,然后加减;
②计算结果要化为最简分式.
新知练习
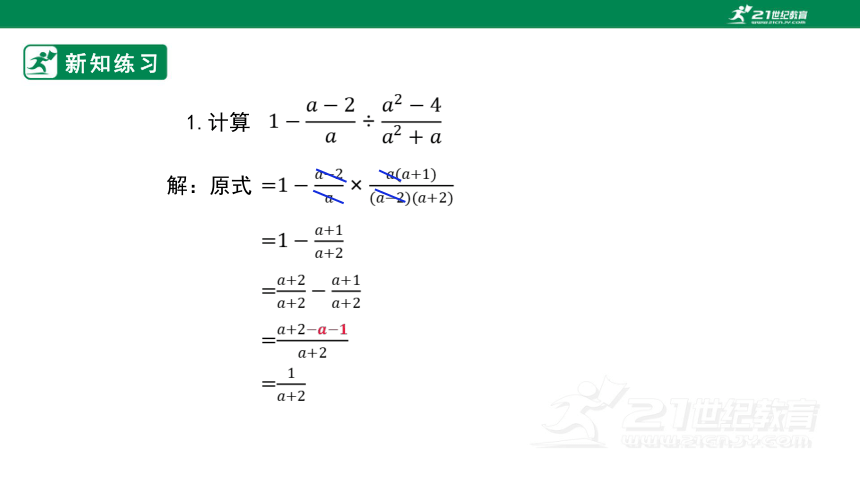
1.计算
解:原式
新知典例
解:(1)原式
例2 计算:
(1) ; (2) .
注意:①要先观察算式,可以看到此题,有小括号,一般先计算括号内的部分。
②为方便后续计算,计算过程中,有可以分解因式的也要分解因式,
新知典例
例2 计算:
(1) ; (2) .
解:(2)原式
新知小结
对于带括号的分式混合运算:
(1)将各分式的分子、分母分解因式后,再进行计算;
(2)先算乘方,再算乘除,最后算加减,若有括号,先算括号内的;
(3)计算结果要化为最简分式或整式.
新知练习
2.化简:(1)
解:原式
新知练习
2.化简:(2)
解:原式
新知探究
例3.用两种方法计算:
=
解:(按运算顺序) 原式
=
(利用乘法分配律)
原式
新知练习
3.化简
解:原式
解:原式
(按运算顺序)
(利用乘法分配律)
新知典例
例4.先化简,再求值: ,从-1,1,2三个数中选一个作为x代入求值。
解:原式
∴x不能为-1和2,
∴x=1,
∴当x=1时,原式
注意:为使分式有意义,只要在分母上出现过的整式都不能为0
新知练习
解:原式
∴x=-2
∴原式= .
课堂总结
分式的运算
分式的混合运算
熟练运用分式的混合运算法则进行计算
先算乘方,再算乘除,最后算加减;若有括号,则先算括号里面的;同级运算,按从左到右的顺序进行计算.
课堂练习
1.(2020·黄冈中考)计算: 的结果是____.
课堂练习
2.计算: .
解:原式
课堂练习
解:原式
3.计算: .
课堂练习
4.计算: .
解:原式
课堂练习
提示:将待化简的式子按照分式的混合运算法则进行计算,然后解不等式组得到x的取值范围,在选取整数解时要注意满足分式有意义的条件,否则不能选取该整数.
课堂练习
解:原式 ,
新知练习
6.先化简,再求值: ,其中 x 满足式子 x2-2x-5=0.
解:原式
∵ x 满足式子x2-2x-5=0, ∴ x2-2x=5.
∴ 原式=5.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
15.2.2 分式的混合运算
人教版八年级上册
知识回顾
分式的加减法法则
同分母分式相加减,分母不变,把分子相加减.
用式子表示:
异分母分式相加减,先通分,变为同分母的分式,再加减.
知识回顾
分式的乘除、乘方混合运算:
分式的乘除、乘方混合运算顺序与分数的乘除、乘方混合运算顺序相同,即先乘方,再乘除,有括号的先算括号里面的.
教学目标
1.掌握分式的混合运算法则和计算步骤.
2.能熟练运用分式的混合运算法则进行计算.
新知导入
同样,我们先类比有理数的混合运算,有理数的混合运算法则是什么?
1.先算乘方,再算乘除,最后算加减;
2.同级运算,按照从左至右的顺序进行;
3.如果有括号,就先算小括号里的,再算中括号里的,然后算大括号里的.
新知探究
知识点 1
分式的混合运算
分式的混合运算
先算乘方,再算乘除,最后算加减;若有括号,则先算括号里面的;同级运算,按从左到右的顺序进行计算.
结合我们已经学习的分式乘除、乘方混合运算法则,可以得出:
新知典例
例1 计算:
解:原式
注意:①要先观察算式,可以看到此题,除平方外,没有其他括号存在,所以先乘方,再乘除,然后加减;
②计算结果要化为最简分式.
新知练习
1.计算
解:原式
新知典例
解:(1)原式
例2 计算:
(1) ; (2) .
注意:①要先观察算式,可以看到此题,有小括号,一般先计算括号内的部分。
②为方便后续计算,计算过程中,有可以分解因式的也要分解因式,
新知典例
例2 计算:
(1) ; (2) .
解:(2)原式
新知小结
对于带括号的分式混合运算:
(1)将各分式的分子、分母分解因式后,再进行计算;
(2)先算乘方,再算乘除,最后算加减,若有括号,先算括号内的;
(3)计算结果要化为最简分式或整式.
新知练习
2.化简:(1)
解:原式
新知练习
2.化简:(2)
解:原式
新知探究
例3.用两种方法计算:
=
解:(按运算顺序) 原式
=
(利用乘法分配律)
原式
新知练习
3.化简
解:原式
解:原式
(按运算顺序)
(利用乘法分配律)
新知典例
例4.先化简,再求值: ,从-1,1,2三个数中选一个作为x代入求值。
解:原式
∴x不能为-1和2,
∴x=1,
∴当x=1时,原式
注意:为使分式有意义,只要在分母上出现过的整式都不能为0
新知练习
解:原式
∴x=-2
∴原式= .
课堂总结
分式的运算
分式的混合运算
熟练运用分式的混合运算法则进行计算
先算乘方,再算乘除,最后算加减;若有括号,则先算括号里面的;同级运算,按从左到右的顺序进行计算.
课堂练习
1.(2020·黄冈中考)计算: 的结果是____.
课堂练习
2.计算: .
解:原式
课堂练习
解:原式
3.计算: .
课堂练习
4.计算: .
解:原式
课堂练习
提示:将待化简的式子按照分式的混合运算法则进行计算,然后解不等式组得到x的取值范围,在选取整数解时要注意满足分式有意义的条件,否则不能选取该整数.
课堂练习
解:原式 ,
新知练习
6.先化简,再求值: ,其中 x 满足式子 x2-2x-5=0.
解:原式
∵ x 满足式子x2-2x-5=0, ∴ x2-2x=5.
∴ 原式=5.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
