高中数学必修第一册人教A版(2019)4.1.2《无理指数幂及实数指数幂的运算》名师课件(共30张PPT)
文档属性
| 名称 | 高中数学必修第一册人教A版(2019)4.1.2《无理指数幂及实数指数幂的运算》名师课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-03 11:48:53 | ||
图片预览






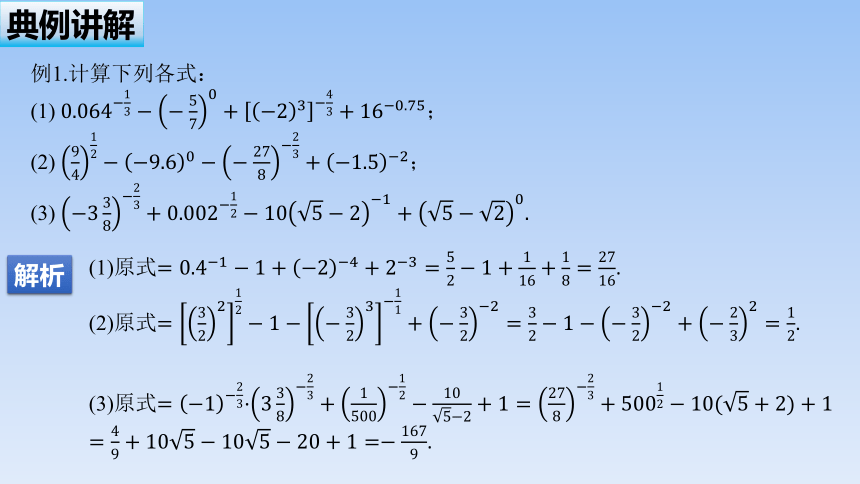


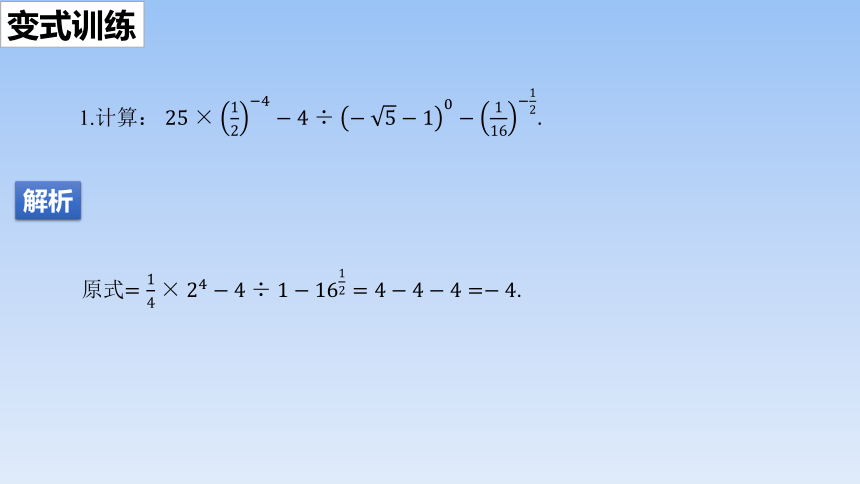
文档简介
(共30张PPT)
n次方根与分数指数幂
根式
根式的概念
根式的性质
根式的运算
根式与分数指数幂的互化
有理数指数幂的运算性质
复习引入
人教A版同步教材名师课件
无理指数幂及实数指数幂的运算
学习目标
学 习 目 标 核心素养
根据具体实例,了解指数的拓展过程. 数学抽象
理解根式的性质,会进行简单的次方根的运算. 数学运算
理解分数指数幂的意义及分数指数幂与根式的互化. 数学抽象
掌握指数的运算性质,会利用整体代换的思想求值. 数学建模
课程目标
1. 理解无理数指数幂的概念;
2. 掌握实数指数幂和根式之间的互化、化简、求值;
3. 掌握实数指数幂的运算性质;
4. 能利用已知条件求值.
数学学科素养
1.数学抽象:无理数指数幂的概念;
2.逻辑推理:实数指数幂和根式之间的互化;
3.数学运算:利用实数指数幂的运算性质化简求值;
4.数据分析:分析已知条件与所求式子之间的联系;
5.数学建模:通过与有理数指数幂性质进行类比,得出无理数指数幂的概念和性质。
学习目标
探究新知
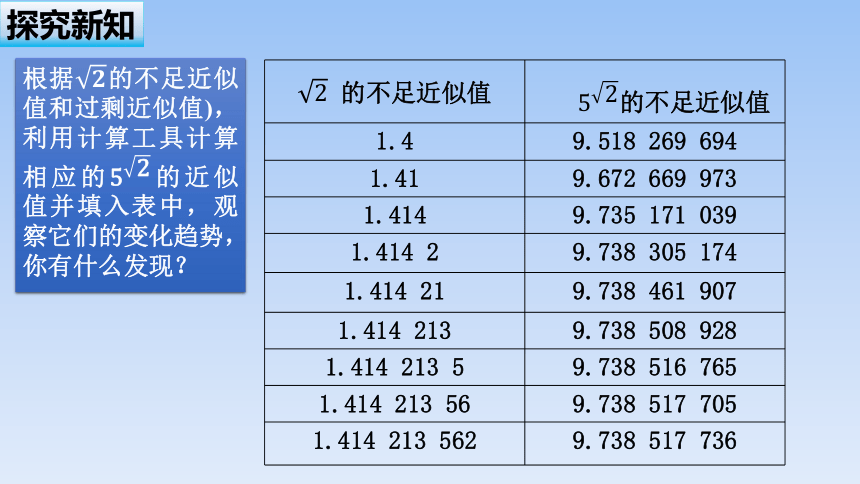
上节课我们将中指数的取值范围从整数拓展到了有理数.那么,当指数是无理数时,的意义是什么?它是一个确定的数吗?如果是,那么它有什么运算性质?
在初中的学习中,我们通过有理数认识了一些无理数.类似地,也可以通过有理数指数幂来认识无理数指数幂.
的不足近似值 的不足近似值
1.4 9.518 269 694
1.41 9.672 669 973
1.414 9.735 171 039
1.414 2 9.738 305 174
1.414 21 9.738 461 907
1.414 213 9.738 508 928
1.414 213 5 9.738 516 765
1.414 213 56 9.738 517 705
1.414 213 562 9.738 517 736
探究新知
根据的不足近似值和过剩近似值),利用计算工具计算相应的的近似值并填入表中,观察它们的变化趋势,你有什么发现?
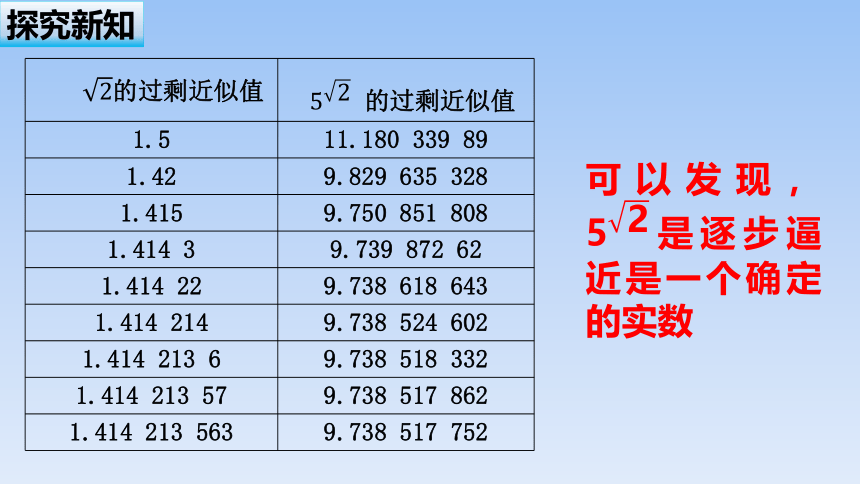
的过剩近似值 的过剩近似值
1.5 11.180 339 89
1.42 9.829 635 328
1.415 9.750 851 808
1.414 3 9.739 872 62
1.414 22 9.738 618 643
1.414 214 9.738 524 602
1.414 213 6 9.738 518 332
1.414 213 57 9.738 517 862
1.414 213 563 9.738 517 752
探究新知
可以发现,是逐步逼近是一个确定的实数
一般地,无理数指数幂( 为无理数)是一个确定的实数,这样,我们就将指数幂( )中指数的取值范围从整数逐步拓展到了实数,实数指数幂是一个确定的实数.
探究新知
整数指数幂的运算性质对实数指数幂同样适用
典例讲解
解析
例1.计算下列各式:
(1)
(2)
(3)
(1)原式.
(2)原式.
(3)原式
.
方法归纳
在进行指数幂的化简、求值时,一般先将根式化成幂的形式,并化小数指数幂为分数指数幂,尽可能地统一成分数指数幂的形式,再利用幂的运算性质进行化简、求值;对于幂的底数,若底数是负数,则先确定符号;若底数是小数,则先化为分数;若底数是带分数,则先化为假分数这样便于运用指数幂的运算性质.
方法归纳
在幂的四则混合运算中,运用乘法公式进行化简,能起到化繁为简的作用.
乘法公式的常用变形:
(1)
(2) ;
(3) ;
(4)
变式训练
解析
1.计算: .
原式.
解析
典例讲解
(1)原式.
(2)原式.
(3)原式
例2、化简下列各式:
(1)
(2) ;
(3) .
方法归纳
幂化简的常用方法和技巧:
把分子、分母分解因式,可约分的先约分;利用公式的基本性质化繁分式为简分式、化异分母为同分母;把适当的几个分式先化简,各个击破;用换元法,使分式简化等.
变式训练
解析
(1)
(2)
2.化简下列各式:
(1) (2) .
.
原式
.
解析
典例讲解
例3、已知求 的值.
原式
方法归纳
解决此类问题的一般步骤:
方法归纳
解条件求值问题的原则:
(1)对于含条件的求值问题,可以把所要求的式子先进行变形,找出与条件的联系,然后求值.
(2)也可以先对条件加以变形,使它与所要求的式子的联系更加明显,从整体上把握代数式的结构特点,然后求值.
变式训练
解析
3.(1)当时,化简;
(2)若求 的值.
(1)原式.
因为,所以原式.
(2)原式,因为,所以原式.
典例讲解
例4、已知,下列各式的值:
(1); (2) ; (3)
解析
(1)将 两边平方,得,即.
(2) 由,得,则 .
(3) ,.
方法归纳
整体思想就是从问题的整体性质出发,突出对问题的整体结构的分析和改造,发现问题的整体结构特征,把某些式子或图形看成一个整体,把握它们的关联,进行有意识的整体处理整体思想在代数式的化简、求值,解方程(组)等方面都有广泛的应用,整体代入、整体运算、整体设元等都是整体思想在数学中的应用.
变式训练
4.(1)已知,则_________.
(2)若,求及的值.
解析
(1) ,,所以,所以.
(2)将两边同时平方,得,即,
所以,因为,.
典例讲解
解析
例5、已知,且,求证:
设,将所要证明的等式的左右两边都化为关于的代数式
令,则,
.
,
.
.
,
,
.
思路分析
方法归纳
指数幂等式的证明问题的解题思路与常用技巧
证明等式A=B的常用思路:
思路一:
思路二:
思路三:
思路四:
.
.
.
.
变式训练
解析
5. ,求证.
,.
所以,
即,
所以.
典例讲解
例6、现有1000元要用于投资,有两种选择:一种是年利率为10%,按单利计算,5年后收回本金和利息;另一种是年利率为9%,按复利计算,5年后收回本金和利息,哪一种投资更有利?这种投资比另一种投资多得利息多少元?
解析
本金1000元,年利率10%,按单利计算,5年后的本息和是元;本金1000元,年利率9%,按复利计算,5年后的本息和为1000(1+9%)3≈1538.6元,由此可知,年利率9%的复利投资比年利率10%的单利投资更有利,5年后多得的利息约为15386-1500=38.6元.
变式训练
6.据美国学者詹姆斯·马丁的测算,在近十年,人类知识总量已达到每三年翻一番,到2020年甚至要达到每73天翻一番的空前速度因此,基础教育的任务已不是教会一切知识,而是让一切人学会学习,已知2000年底,人类知识总量为a,假如从2000年底到2009年底是每三年翻一番,从2009年底到2019年底是每一年翻一番,2020年是每73天翻一番,试回答:
(1)求2009年底人类知识总量;
(2)求2019年底人类知识总量;
(3)2020年按365天计算,2020年底人类知识总量是多少?
解析
∵翻一番是在原来的基础上乘2,翻两番是在原来的基础上乘4,即 ,……,翻n番在原来的基础上乘 ,于是:(1)从2000年底到2009年底是每三年翻一番,共翻了三番,所以2009年底人类知识总量为 (2)从2009年底到2019年底是每一年翻番,共翻十番,所以2019年底人类知识总量为 (3)2020年是73天翻一番,共翻五番,所以2020年底人类知识总量为
.
.
.
当堂练习
A
B
3.
B
.
.
.
1. ( )
的指数幂表示为
2.
化简的结果是( )
.
.
计算 ( )
.
归纳小结
实数指数幂的运算性质
作 业
P109练习:1
P110习题4.1:7、8
n次方根与分数指数幂
根式
根式的概念
根式的性质
根式的运算
根式与分数指数幂的互化
有理数指数幂的运算性质
复习引入
人教A版同步教材名师课件
无理指数幂及实数指数幂的运算
学习目标
学 习 目 标 核心素养
根据具体实例,了解指数的拓展过程. 数学抽象
理解根式的性质,会进行简单的次方根的运算. 数学运算
理解分数指数幂的意义及分数指数幂与根式的互化. 数学抽象
掌握指数的运算性质,会利用整体代换的思想求值. 数学建模
课程目标
1. 理解无理数指数幂的概念;
2. 掌握实数指数幂和根式之间的互化、化简、求值;
3. 掌握实数指数幂的运算性质;
4. 能利用已知条件求值.
数学学科素养
1.数学抽象:无理数指数幂的概念;
2.逻辑推理:实数指数幂和根式之间的互化;
3.数学运算:利用实数指数幂的运算性质化简求值;
4.数据分析:分析已知条件与所求式子之间的联系;
5.数学建模:通过与有理数指数幂性质进行类比,得出无理数指数幂的概念和性质。
学习目标
探究新知
上节课我们将中指数的取值范围从整数拓展到了有理数.那么,当指数是无理数时,的意义是什么?它是一个确定的数吗?如果是,那么它有什么运算性质?
在初中的学习中,我们通过有理数认识了一些无理数.类似地,也可以通过有理数指数幂来认识无理数指数幂.
的不足近似值 的不足近似值
1.4 9.518 269 694
1.41 9.672 669 973
1.414 9.735 171 039
1.414 2 9.738 305 174
1.414 21 9.738 461 907
1.414 213 9.738 508 928
1.414 213 5 9.738 516 765
1.414 213 56 9.738 517 705
1.414 213 562 9.738 517 736
探究新知
根据的不足近似值和过剩近似值),利用计算工具计算相应的的近似值并填入表中,观察它们的变化趋势,你有什么发现?
的过剩近似值 的过剩近似值
1.5 11.180 339 89
1.42 9.829 635 328
1.415 9.750 851 808
1.414 3 9.739 872 62
1.414 22 9.738 618 643
1.414 214 9.738 524 602
1.414 213 6 9.738 518 332
1.414 213 57 9.738 517 862
1.414 213 563 9.738 517 752
探究新知
可以发现,是逐步逼近是一个确定的实数
一般地,无理数指数幂( 为无理数)是一个确定的实数,这样,我们就将指数幂( )中指数的取值范围从整数逐步拓展到了实数,实数指数幂是一个确定的实数.
探究新知
整数指数幂的运算性质对实数指数幂同样适用
典例讲解
解析
例1.计算下列各式:
(1)
(2)
(3)
(1)原式.
(2)原式.
(3)原式
.
方法归纳
在进行指数幂的化简、求值时,一般先将根式化成幂的形式,并化小数指数幂为分数指数幂,尽可能地统一成分数指数幂的形式,再利用幂的运算性质进行化简、求值;对于幂的底数,若底数是负数,则先确定符号;若底数是小数,则先化为分数;若底数是带分数,则先化为假分数这样便于运用指数幂的运算性质.
方法归纳
在幂的四则混合运算中,运用乘法公式进行化简,能起到化繁为简的作用.
乘法公式的常用变形:
(1)
(2) ;
(3) ;
(4)
变式训练
解析
1.计算: .
原式.
解析
典例讲解
(1)原式.
(2)原式.
(3)原式
例2、化简下列各式:
(1)
(2) ;
(3) .
方法归纳
幂化简的常用方法和技巧:
把分子、分母分解因式,可约分的先约分;利用公式的基本性质化繁分式为简分式、化异分母为同分母;把适当的几个分式先化简,各个击破;用换元法,使分式简化等.
变式训练
解析
(1)
(2)
2.化简下列各式:
(1) (2) .
.
原式
.
解析
典例讲解
例3、已知求 的值.
原式
方法归纳
解决此类问题的一般步骤:
方法归纳
解条件求值问题的原则:
(1)对于含条件的求值问题,可以把所要求的式子先进行变形,找出与条件的联系,然后求值.
(2)也可以先对条件加以变形,使它与所要求的式子的联系更加明显,从整体上把握代数式的结构特点,然后求值.
变式训练
解析
3.(1)当时,化简;
(2)若求 的值.
(1)原式.
因为,所以原式.
(2)原式,因为,所以原式.
典例讲解
例4、已知,下列各式的值:
(1); (2) ; (3)
解析
(1)将 两边平方,得,即.
(2) 由,得,则 .
(3) ,.
方法归纳
整体思想就是从问题的整体性质出发,突出对问题的整体结构的分析和改造,发现问题的整体结构特征,把某些式子或图形看成一个整体,把握它们的关联,进行有意识的整体处理整体思想在代数式的化简、求值,解方程(组)等方面都有广泛的应用,整体代入、整体运算、整体设元等都是整体思想在数学中的应用.
变式训练
4.(1)已知,则_________.
(2)若,求及的值.
解析
(1) ,,所以,所以.
(2)将两边同时平方,得,即,
所以,因为,.
典例讲解
解析
例5、已知,且,求证:
设,将所要证明的等式的左右两边都化为关于的代数式
令,则,
.
,
.
.
,
,
.
思路分析
方法归纳
指数幂等式的证明问题的解题思路与常用技巧
证明等式A=B的常用思路:
思路一:
思路二:
思路三:
思路四:
.
.
.
.
变式训练
解析
5. ,求证.
,.
所以,
即,
所以.
典例讲解
例6、现有1000元要用于投资,有两种选择:一种是年利率为10%,按单利计算,5年后收回本金和利息;另一种是年利率为9%,按复利计算,5年后收回本金和利息,哪一种投资更有利?这种投资比另一种投资多得利息多少元?
解析
本金1000元,年利率10%,按单利计算,5年后的本息和是元;本金1000元,年利率9%,按复利计算,5年后的本息和为1000(1+9%)3≈1538.6元,由此可知,年利率9%的复利投资比年利率10%的单利投资更有利,5年后多得的利息约为15386-1500=38.6元.
变式训练
6.据美国学者詹姆斯·马丁的测算,在近十年,人类知识总量已达到每三年翻一番,到2020年甚至要达到每73天翻一番的空前速度因此,基础教育的任务已不是教会一切知识,而是让一切人学会学习,已知2000年底,人类知识总量为a,假如从2000年底到2009年底是每三年翻一番,从2009年底到2019年底是每一年翻一番,2020年是每73天翻一番,试回答:
(1)求2009年底人类知识总量;
(2)求2019年底人类知识总量;
(3)2020年按365天计算,2020年底人类知识总量是多少?
解析
∵翻一番是在原来的基础上乘2,翻两番是在原来的基础上乘4,即 ,……,翻n番在原来的基础上乘 ,于是:(1)从2000年底到2009年底是每三年翻一番,共翻了三番,所以2009年底人类知识总量为 (2)从2009年底到2019年底是每一年翻番,共翻十番,所以2019年底人类知识总量为 (3)2020年是73天翻一番,共翻五番,所以2020年底人类知识总量为
.
.
.
当堂练习
A
B
3.
B
.
.
.
1. ( )
的指数幂表示为
2.
化简的结果是( )
.
.
计算 ( )
.
归纳小结
实数指数幂的运算性质
作 业
P109练习:1
P110习题4.1:7、8
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
