人教版2019必修一 5.1.1 弧度制 课件(21张PPT)
文档属性
| 名称 | 人教版2019必修一 5.1.1 弧度制 课件(21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-03 12:55:53 | ||
图片预览






文档简介
(共21张PPT)
弧 度 制
NBA官方数据
身高:7英尺6英寸,体重:310磅;
中国篮协数据
身高:2.26米 ,体重:140.6公斤.
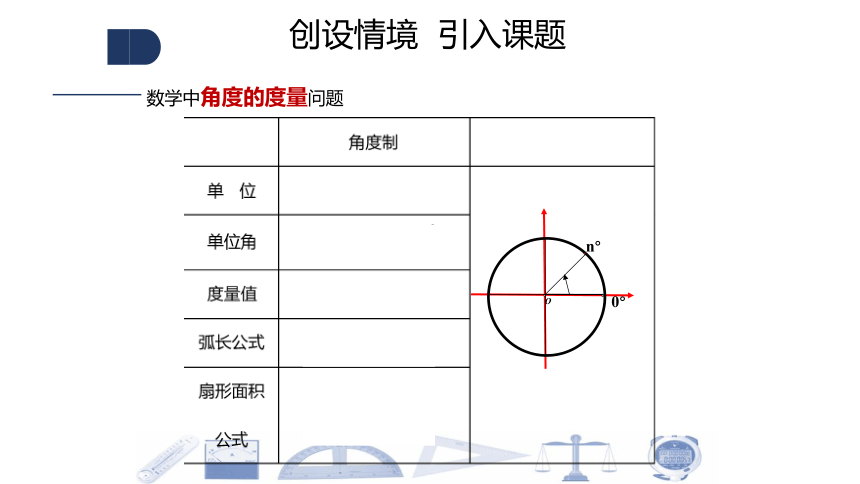
数学中角度的度量问题
创设情境 引入课题
O
0°
n°
圆心角不变,比值不变.
比值的大小与所取圆的半径大小无关
圆心角改变,比值改变.
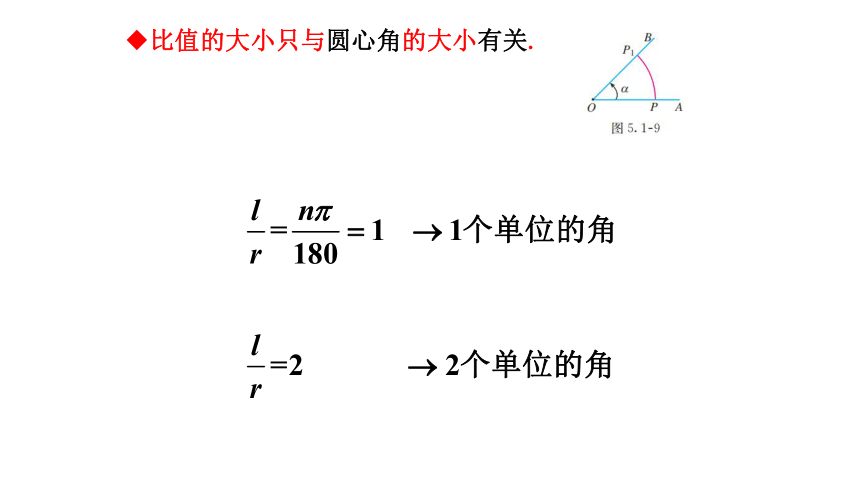
比值的大小只与圆心角的大小有关.
比值的大小只与圆心角的大小有关.
归纳探索 形成概念
概念
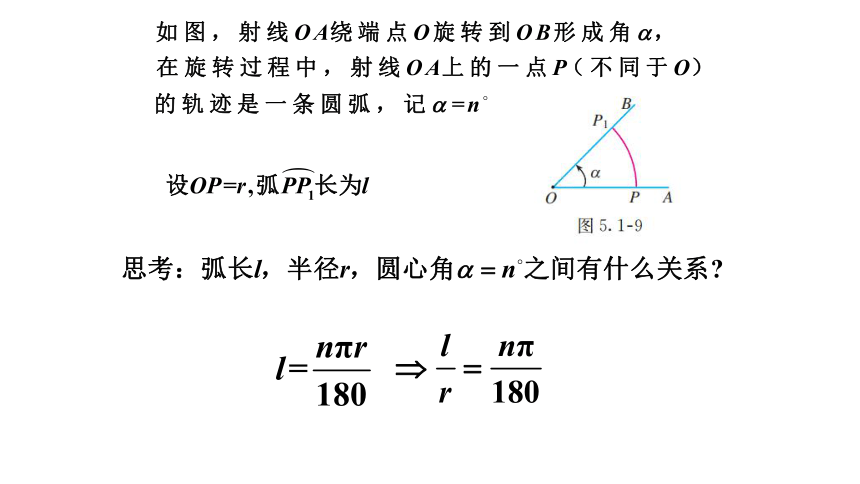
问题本源
任意角的形成过程
探究发现: 圆心角α 的大小是由所对应的弧长与半径的比值唯一确定的,与半径大小无关
半圆所对的圆心角为多少弧度?
角度制与弧度制换算(不能混用)
整圆所对的圆心角
半圆所对的圆心角
合作探究 理解概念
探 究
数学中角度的度量问题
范例选讲 深化概念
思考:2rad,3rad, 4rad, 5rad的角分别在哪个象限?
范例选讲 深化概念
角度
弧度
注意
拓展深化 提升认识
正角
零角
负角
正实数
0
负实数
任意角的集合
实数集R
表示范围问题
用弧度制表示终边在下列阴影部分的角:
1、逆时针转动
2、注意虚线与实线的区别
3、注意一圈出现的次数
思考:对应的弦长是多少?
能否探究出更一般的规律?
例4
写出满足下列条件的角的集合(用弧度制):
1、 终边与X轴非负半轴重合;
2、 终边与X轴非正半轴重合;
3、 终边与X轴重合;
4、 终边与Y轴非负半轴重合;
5、 终边与Y轴非正半轴重合;
6、 终边与Y轴重合;
7、第一象限内的角;
8、第二象限内的角;
9、第三象限内的角;
10、第四象限内的角;
练习
x
y
0
(1)
x
y
0
(2)
弧 度 制
NBA官方数据
身高:7英尺6英寸,体重:310磅;
中国篮协数据
身高:2.26米 ,体重:140.6公斤.
数学中角度的度量问题
创设情境 引入课题
O
0°
n°
圆心角不变,比值不变.
比值的大小与所取圆的半径大小无关
圆心角改变,比值改变.
比值的大小只与圆心角的大小有关.
比值的大小只与圆心角的大小有关.
归纳探索 形成概念
概念
问题本源
任意角的形成过程
探究发现: 圆心角α 的大小是由所对应的弧长与半径的比值唯一确定的,与半径大小无关
半圆所对的圆心角为多少弧度?
角度制与弧度制换算(不能混用)
整圆所对的圆心角
半圆所对的圆心角
合作探究 理解概念
探 究
数学中角度的度量问题
范例选讲 深化概念
思考:2rad,3rad, 4rad, 5rad的角分别在哪个象限?
范例选讲 深化概念
角度
弧度
注意
拓展深化 提升认识
正角
零角
负角
正实数
0
负实数
任意角的集合
实数集R
表示范围问题
用弧度制表示终边在下列阴影部分的角:
1、逆时针转动
2、注意虚线与实线的区别
3、注意一圈出现的次数
思考:对应的弦长是多少?
能否探究出更一般的规律?
例4
写出满足下列条件的角的集合(用弧度制):
1、 终边与X轴非负半轴重合;
2、 终边与X轴非正半轴重合;
3、 终边与X轴重合;
4、 终边与Y轴非负半轴重合;
5、 终边与Y轴非正半轴重合;
6、 终边与Y轴重合;
7、第一象限内的角;
8、第二象限内的角;
9、第三象限内的角;
10、第四象限内的角;
练习
x
y
0
(1)
x
y
0
(2)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
