人教版2019必修一 两角差的余弦公式 课件(共26张PPT)
文档属性
| 名称 | 人教版2019必修一 两角差的余弦公式 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-04 09:43:33 | ||
图片预览




文档简介
(共26张PPT)
两角差的余弦公式
A
o
x
y
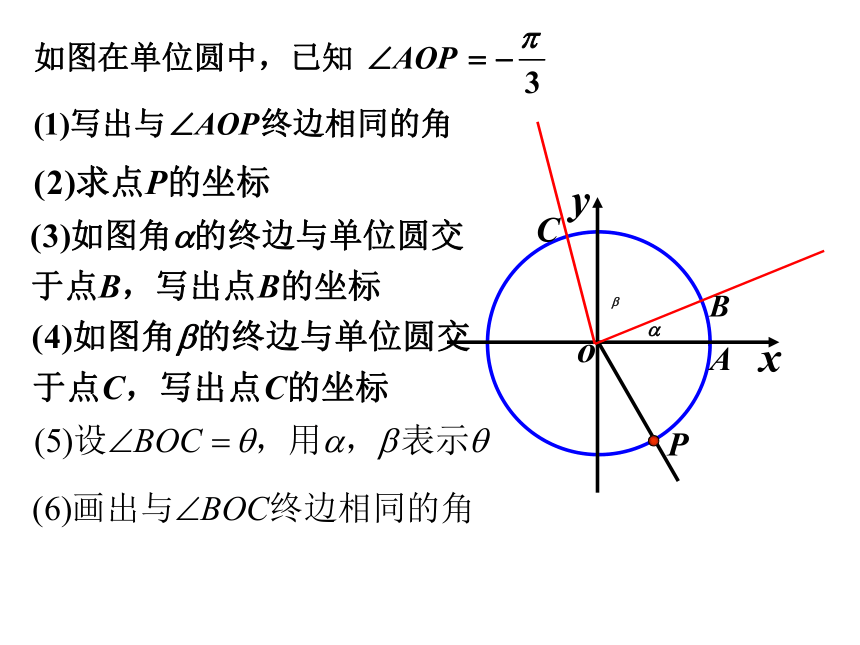
A
o
y
x
P
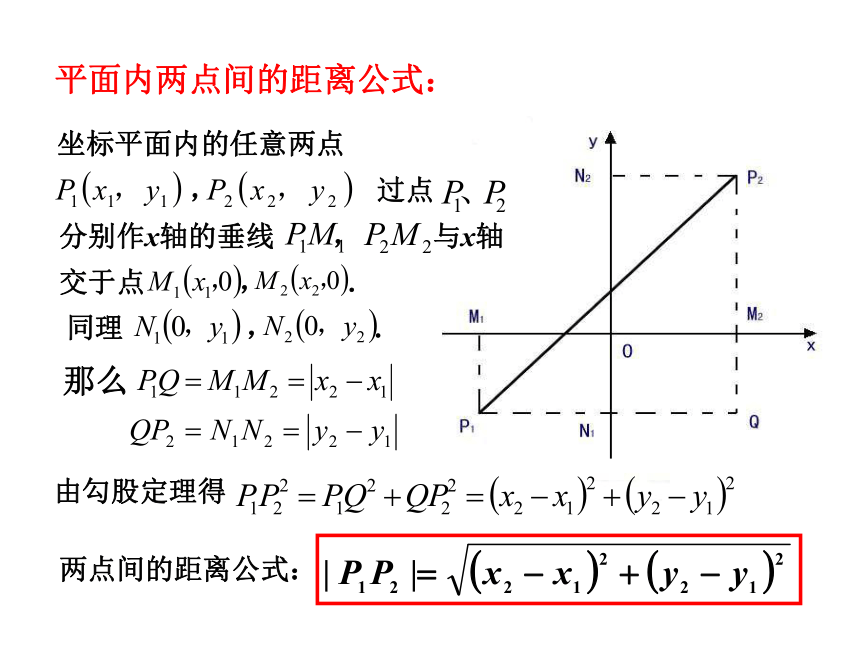
由勾股定理得
那么
两点间的距离公式:
平面内两点间的距离公式:
坐标平面内的任意两点
, 过点
分别作x轴的垂线 , 与x轴
交于点 , .
同理 , .
∴
两角差的余弦公式
差角的余弦公式
①任意角; ②同名积; ③符号反.
说一说:1、公式的结构特点:
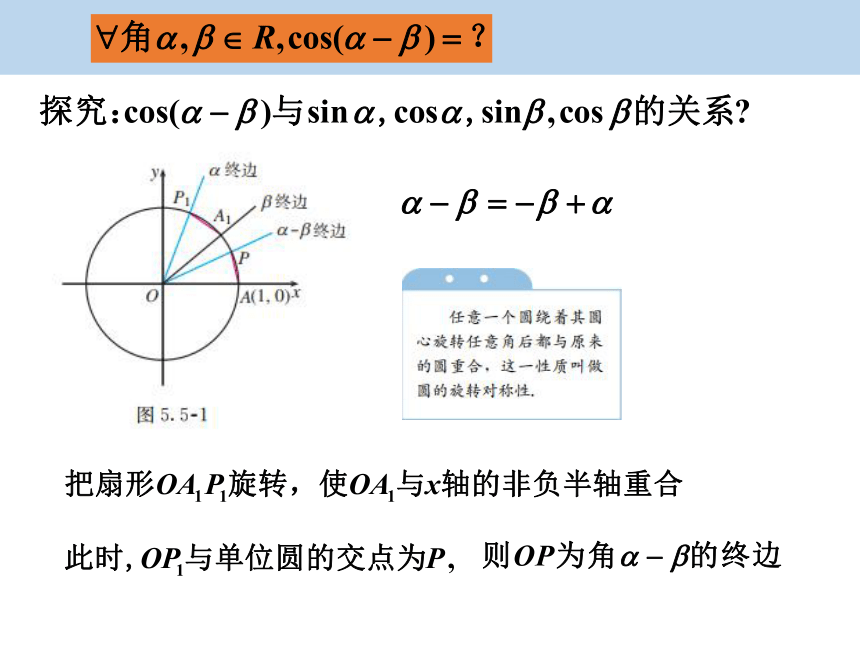
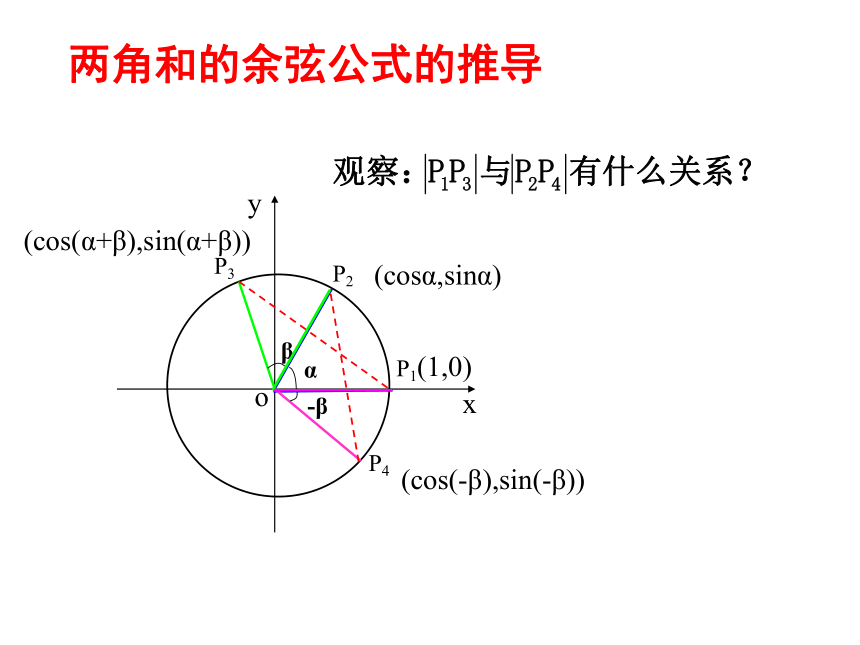
两角和的余弦公式的推导
x
y
o
P1
P2
α
β
P4
P3
-β
(1,0)
(cosα,sinα)
(cos(α+β),sin(α+β))
(cos(-β),sin(-β))
观察:
x
y
o
P1
P2
α
β
P4
P3
-β
(1,0)
(cosα,sinα)
(cos(-β),sin(-β))
(cos(α+β),sin(α+β))
x
y
P1
P2
P3
P4
O
P1P3=
P2P4=
由P1P3=P2P4 得 P1P32=P2P42
即:
展开,得
得
得
得
和角的余弦公式
分析:
学以致用
典例分析
典例分析
典例分析
例3:
变角:
分析:
典例分析
例4
典例分析
课堂小结
(2)正用和逆用两角差的余弦公式;
两角差的余弦公式
(3)未知角与已知角的转化;
(4)注意角的范围和三角函数值的正负.
(1)从锐角到任意的角,知识和方法的迁移;
①任意角; ②同名积; ③符号反.
两角差的余弦公式
A
o
x
y
A
o
y
x
P
由勾股定理得
那么
两点间的距离公式:
平面内两点间的距离公式:
坐标平面内的任意两点
, 过点
分别作x轴的垂线 , 与x轴
交于点 , .
同理 , .
∴
两角差的余弦公式
差角的余弦公式
①任意角; ②同名积; ③符号反.
说一说:1、公式的结构特点:
两角和的余弦公式的推导
x
y
o
P1
P2
α
β
P4
P3
-β
(1,0)
(cosα,sinα)
(cos(α+β),sin(α+β))
(cos(-β),sin(-β))
观察:
x
y
o
P1
P2
α
β
P4
P3
-β
(1,0)
(cosα,sinα)
(cos(-β),sin(-β))
(cos(α+β),sin(α+β))
x
y
P1
P2
P3
P4
O
P1P3=
P2P4=
由P1P3=P2P4 得 P1P32=P2P42
即:
展开,得
得
得
得
和角的余弦公式
分析:
学以致用
典例分析
典例分析
典例分析
例3:
变角:
分析:
典例分析
例4
典例分析
课堂小结
(2)正用和逆用两角差的余弦公式;
两角差的余弦公式
(3)未知角与已知角的转化;
(4)注意角的范围和三角函数值的正负.
(1)从锐角到任意的角,知识和方法的迁移;
①任意角; ②同名积; ③符号反.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
