人教版2019选修一2.1.1 直线的倾斜角与斜率 课件(32张PPT)
文档属性
| 名称 | 人教版2019选修一2.1.1 直线的倾斜角与斜率 课件(32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-04 05:00:21 | ||
图片预览










文档简介
(共32张PPT)
几何图形的性质主要指图形的形状、大小和位置关系等.研究几何图形的性质有很多方法.在以往的几何学习中,我们常常通过直观感知、操作确以思辨论证、度量计算等研究它们,这种借助图形的直观,在一些基本名词(如点、直线、平面等)基础上,以一些公理与公设为依据,运用同一律、矛盾律和排中律,以及大前提、小前提、结论的“三段论”式的逻辑规则,经过一定的推理,导出一系列命题的研究方法,常常称为综合法
本章我们采用坐标法研究几何形的性质.
坐标法是解析几何中最基本的研究方法.
解析几何是17世纪法国数学家笛卡儿和费马创立的,它基本内涵和方法是:通过坐标系,把几何的基本元素 -- 点和数的基本对象 -- 数(有序数对或数组)对应起来,在此基础驶立曲线(点的轨迹)的方程,从而把几何问题转化为代数题,再通过代数方法研究几何图形的性质.解析几何的创立是学发展史上的一个里程碑,数学从此进入变量数学时期,它为像积分的创建奠定了基础.
在用坐标法研究几何图形性质的过程中,常常把图形看成点的集合或点运动形成的轨迹.点是构成图形的基本元素,在平面直角坐标系中,用有序数对表示,一个有序数对表示唯一的一点,也就是说,点与有序数对一一对应.
直线和圆是平面上最简单的非封闭图形和“曲线型”闭图形.用点的坐标刻画直线和圆的几何特征,就得到它们的点(x,y)满足的规律,这个规律用代数表达式
f(x,y) = 0表示,就建立了直和圆的方程.由直线(圆)上每一个点的坐标(x,y)都满足方程,以方程的解为坐标的点都在直线(圆)上,确立了直线(圆)与其方程之间的关系:直线(圆)可以由方程表示,相应的方程表示直线(圆).从而,可以由直线和圆的方程研究与它们相关的几何性质.
可以由直线和圆的方程研究与它们相关的几何性质.这种研究几何图质的过程,教科书用一个非常形象的词“三步曲”来概括:
第一步:建立适当的平面直角坐标系,用坐标和方程表示问题中的几何元素,把平面几题转化为代数问题;
第二步:通过代数运算,解决代数问题;
第三步:把代数运算的结果“翻译”成几何结论.
“三步曲”说的是坐标法解决几何问题的程序性.普适性是指一旦直线和圆的方程确么它们的主要几何性质,如距离、角度等原则上可以由它们的方程得到,而综合法处理这些问题时有时需要很强的技巧,往往“就事论事”.
本章我们将在平面直角坐标系中,探索确定直线位置的几何要素,建立直线的方程,并通过直线的方程研究两条直线的位置关系、交点坐标以及点到直线的距离等.类似地,通过确定圆的几何要素,建立圆的方程,再通过圆的方程研究与圆相关的问题;最后应用直线和圆的方程解决一些实际问题.
我们知道,点是构成直线的基本元素.在平面直角坐标系中,可以用坐标表示点,那么,如何用坐标表示直线呢 为了用代数方法研究直线的有关问题,本节我们首先在平面直角坐标系中探索确定直线位置的几何要素,然后用代数方法把这些几何要素表示出来.
2.1直线的倾斜角与斜率
2.1直线的倾斜角与斜率
2.1.1倾斜角与斜率1.能解释直线的倾斜角和斜率的概念,描述两者之间的相互转换关系.2.能说明倾斜角是刻画直线倾斜程度和确定直线的几何要素,并能根据斜率(倾斜角)的范围判断倾斜角(斜率)的范围.3.能推导得出直线斜率的计算公式,并能灵活运用公式计算直线的斜率教学目标问题情境直线—最简单的几何图形飞逝的流星沿不同的方向运动在空中形成美丽的直线1.确定一条直线的几何要素是什么
思考?
.
x
y
o
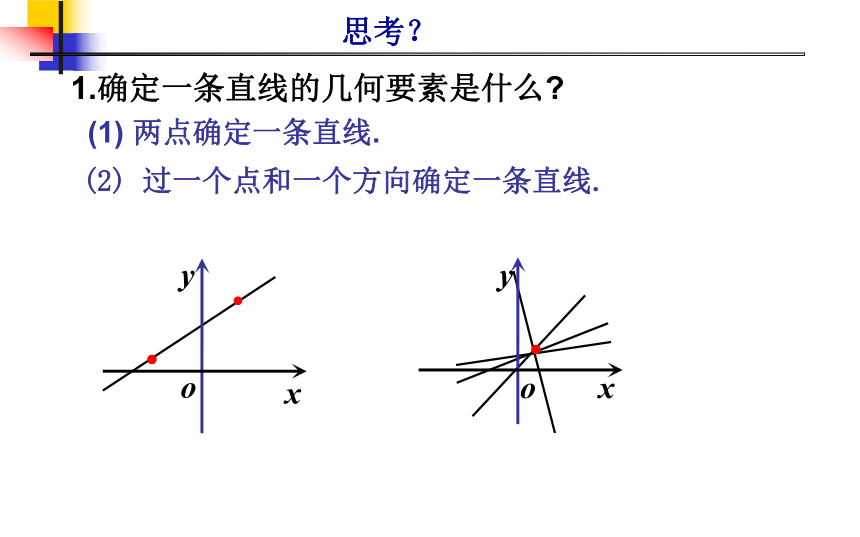
(1) 两点确定一条直线.
(2) 过一个点和一个方向确定一条直线.
.
.
y
x
o
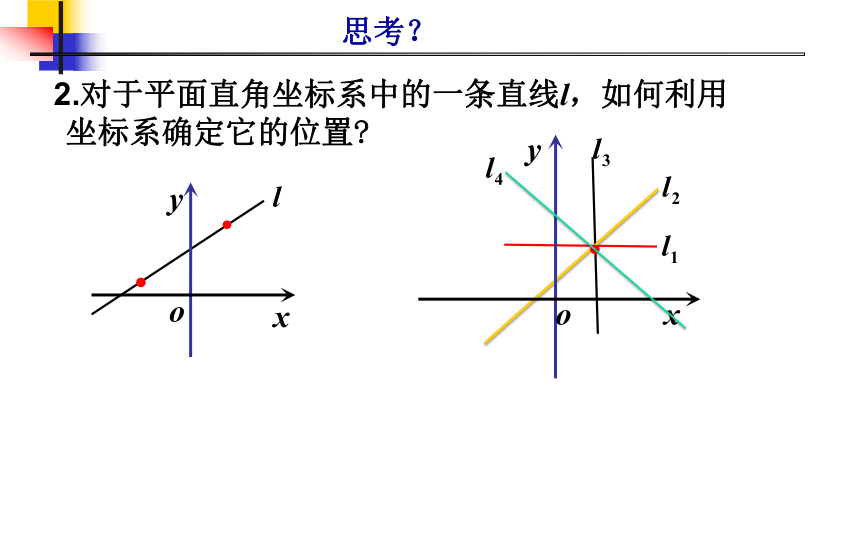
2.对于平面直角坐标系中的一条直线l,如何利用坐标系确定它的位置
思考?
.
x
y
o
.
.
y
x
o
一、直线的倾斜角
1.直线倾斜角的定义:
当直线 l 与x轴相交时,我们取x轴作为基准,x轴正向与直线l 向上方向之间所成的角叫做直线的倾斜角
注意: (1)直线向上方向;
(2)x轴的正方向。
倾斜角α的范围为:
.
y
x
o
这样,在平面直角坐标系中,每一条直线都有一个确定的倾斜角,而且方向相同的直线,其倾斜程度相同,斜角相等;方向不同的直线,其倾斜程度不同,倾斜角不相等
探究?
我们把一条直线倾斜角 的正切叫做这条直线的斜率。斜率通常用k表示,即:
直线的斜率
2
3
2
o
2
-
y
x
直线的斜率
倾斜角α不是90°的直线都有斜率,并且倾斜角不同,直线的斜率也不同.因此,可以用斜率表示直线的倾斜程度.
我们把一条直线倾斜角 的正切叫做这条直线的斜率。斜率通常用k表示,即:
(1)若一条直线的倾斜角为90°,则这条直线与x轴垂直. ( )
(2)任何一条直线有且只有一个倾斜角和它对应. ( )
√
×
【诊断分析】 1.判断正误.(请在括号中打“√”或“×”)
(3)零向量可以作为直线的方向向量. ( )
√
(4)直线的倾斜角是锐角时,直线的斜率为正;直线的倾斜角是钝角时,
直线的斜率为负.
(5)直线的倾斜角越大,它的斜率也越大;反过来,直线的斜率越大,
它的倾斜角也越大.
(6)所有的直线都有倾斜角,但不是所有的直线都有斜率,
倾斜角是90°的直线不存在斜率. ( )
探究点一 直线的倾斜角问题
例1 (1)如图2-1-1(1)和(2),直线l1和l2的倾斜角分别是 ( )
A.140°,104° B.150°,104°
C.150°,106° D.130°,106°
D
(2)若过点P(1,1+a)和Q(3,2a)的直线的倾斜角α为钝角,求实数a的取值范围.
(3)已知直线l的倾斜角α=45°,且P1(2,y1),P2(x2,5),P3(3,1)是直线l上的三点,求x2,y1的值.
变式 (1)一条直线l与x轴相交,其向上的方向与x轴的负方向所成的角为α,则l的倾斜角为 ( )
A.α B.180°-α C.90°+α D.90°+α或90°-α
课 中 探 究
B
(2)直线l1⊥l2,若直线l1的倾斜角为α,直线l2的倾斜角为β(β>α),则下列说法正确的是 ( )
A.β-α=90° B.α+β=90°
C.α+β=180° D.β-α为锐角
A
(3) 已知直线l经过点A(0,1),B(sin α,0),求直线l的倾斜角θ的取值范围.
拓展 已知两点A(-3,4),B(3,2),过点P(1,0)的直线l与线段AB有公共点,则直线l的斜率k的取值范围是 ,直线l的倾斜角α的取值范围是 .
k≤-1或k≥1
45°≤α≤135°
探究点二 求直线的斜率问题
例2 (1)直线l过点A(1,2),且不过第四象限,则
直线l的斜率的取值范围是 ( )
A.[0,2] B.[0,1]
C. D.
A
(2)已知直线l1的方向向量为n=(2,1),直线l2的倾斜角是直线l1的倾斜角的2倍,求直线l2的斜率.
变式 (1)过点A(m2-n2,m2+n2)和点B(2mn-2n2,2mn)(m≠n)的直线的斜率是 .
1
(2)已知A(a,2),B(5,1),C(-4,2a)三点在同一条直线上,则a的值是 .
2或
拓展2 已知实数x,y满足y=x2-x+2(-1≤x≤1),试求的最大值和最小值.
拓展1 若点P(x,y)在以A(2,4),B(3,2)为端点的线段上,
求的最大值和最小值.
探究点三 直线的方向向量的应用
例3 (1)已知经过两点A(2,3),B(4,5)的直线的一个方向向量为(1,k),则k的值为 .
1
(2)已知直线l的一个方向向量为(2,4),则直线l的斜率为 .
2
1.已知直线l的斜率的绝对值等于,则直线l的倾斜角为( )
A.60° B.30° C.60°或120° D.30°或150°
课 堂 评 价
C
2.过两点A(1,),B(4,2)的直线的倾斜角为 ( )
A.30° B.60° C.120° D.150°
A
3.已知直线l的倾斜角为α-15°,则下列结论中正确的是 ( )
A.0°≤α<180° B.15°<α<180° C.15°≤α<180° D.15°≤α<195°
D
4.若经过A(m,3),B(1,2)两点的直线的一个方向向量为(-3,-3),则m等于 ( )
A.2 B.1 C.-1 D.-2
A
6.直线L的倾斜角是连接(3,-5),(0,-9)两点的直线的倾斜角的两倍,求直线L的斜率。
课 堂 评 价
5.求过点M(0,2)和N(2,3m2+12m+13)(m∈R)的直线l的斜率k的取值范围。解:由斜率公式得直线l的斜率知识小结
1、直线的倾斜角的定义
2、直线的斜率的定义
3、两点间斜率公式
当直线 l 与x轴相交时,
我们取x轴作为基准,
x轴正向与直线 l 向上
方向之间所成的角α
叫做直线 l 的倾斜角.
一条直线的倾斜角 的正切值叫做这条
直线的斜率.
1.倾斜角的定义解读
(1)倾斜角的定义含有三个条件:①直线向上的方向;②x轴正方向;③小于平角的非负角.
(2)倾斜角从“形”的方面直观地体现了直线对于x轴的倾斜程度.
(3)平面直角坐标系内每一条直线都有一个确定的倾斜角,且倾斜程度相同的直线倾斜角相等;倾斜程度不同的直线,其倾斜角不相等.直线与倾斜角是多对一的关系.
2.直线的倾斜角与斜率的关系
(1)直线都存在唯一的倾斜角,但并不是每条直线都存在斜率,倾斜角为90°的直线没有斜率.
(2)直线的倾斜角是一个角(图形),而斜率是一个实数值(数),斜率的绝对值越大,直线的倾斜角越接近90°.
(3)不同的倾斜角对应不同的斜率,因此,要确定一条不垂直于x轴的直线,只要知道直线上一个定点和它的斜率即可.
3.直线方向向量与斜率的关系
(1)当直线的斜率存在时,直线的方向向量与向量(1,k)共线.
(2)当直线的斜率不存在时,直线的方向向量与向量(0,1)共线.
几何图形的性质主要指图形的形状、大小和位置关系等.研究几何图形的性质有很多方法.在以往的几何学习中,我们常常通过直观感知、操作确以思辨论证、度量计算等研究它们,这种借助图形的直观,在一些基本名词(如点、直线、平面等)基础上,以一些公理与公设为依据,运用同一律、矛盾律和排中律,以及大前提、小前提、结论的“三段论”式的逻辑规则,经过一定的推理,导出一系列命题的研究方法,常常称为综合法
本章我们采用坐标法研究几何形的性质.
坐标法是解析几何中最基本的研究方法.
解析几何是17世纪法国数学家笛卡儿和费马创立的,它基本内涵和方法是:通过坐标系,把几何的基本元素 -- 点和数的基本对象 -- 数(有序数对或数组)对应起来,在此基础驶立曲线(点的轨迹)的方程,从而把几何问题转化为代数题,再通过代数方法研究几何图形的性质.解析几何的创立是学发展史上的一个里程碑,数学从此进入变量数学时期,它为像积分的创建奠定了基础.
在用坐标法研究几何图形性质的过程中,常常把图形看成点的集合或点运动形成的轨迹.点是构成图形的基本元素,在平面直角坐标系中,用有序数对表示,一个有序数对表示唯一的一点,也就是说,点与有序数对一一对应.
直线和圆是平面上最简单的非封闭图形和“曲线型”闭图形.用点的坐标刻画直线和圆的几何特征,就得到它们的点(x,y)满足的规律,这个规律用代数表达式
f(x,y) = 0表示,就建立了直和圆的方程.由直线(圆)上每一个点的坐标(x,y)都满足方程,以方程的解为坐标的点都在直线(圆)上,确立了直线(圆)与其方程之间的关系:直线(圆)可以由方程表示,相应的方程表示直线(圆).从而,可以由直线和圆的方程研究与它们相关的几何性质.
可以由直线和圆的方程研究与它们相关的几何性质.这种研究几何图质的过程,教科书用一个非常形象的词“三步曲”来概括:
第一步:建立适当的平面直角坐标系,用坐标和方程表示问题中的几何元素,把平面几题转化为代数问题;
第二步:通过代数运算,解决代数问题;
第三步:把代数运算的结果“翻译”成几何结论.
“三步曲”说的是坐标法解决几何问题的程序性.普适性是指一旦直线和圆的方程确么它们的主要几何性质,如距离、角度等原则上可以由它们的方程得到,而综合法处理这些问题时有时需要很强的技巧,往往“就事论事”.
本章我们将在平面直角坐标系中,探索确定直线位置的几何要素,建立直线的方程,并通过直线的方程研究两条直线的位置关系、交点坐标以及点到直线的距离等.类似地,通过确定圆的几何要素,建立圆的方程,再通过圆的方程研究与圆相关的问题;最后应用直线和圆的方程解决一些实际问题.
我们知道,点是构成直线的基本元素.在平面直角坐标系中,可以用坐标表示点,那么,如何用坐标表示直线呢 为了用代数方法研究直线的有关问题,本节我们首先在平面直角坐标系中探索确定直线位置的几何要素,然后用代数方法把这些几何要素表示出来.
2.1直线的倾斜角与斜率
2.1直线的倾斜角与斜率
2.1.1倾斜角与斜率1.能解释直线的倾斜角和斜率的概念,描述两者之间的相互转换关系.2.能说明倾斜角是刻画直线倾斜程度和确定直线的几何要素,并能根据斜率(倾斜角)的范围判断倾斜角(斜率)的范围.3.能推导得出直线斜率的计算公式,并能灵活运用公式计算直线的斜率教学目标问题情境直线—最简单的几何图形飞逝的流星沿不同的方向运动在空中形成美丽的直线1.确定一条直线的几何要素是什么
思考?
.
x
y
o
(1) 两点确定一条直线.
(2) 过一个点和一个方向确定一条直线.
.
.
y
x
o
2.对于平面直角坐标系中的一条直线l,如何利用坐标系确定它的位置
思考?
.
x
y
o
.
.
y
x
o
一、直线的倾斜角
1.直线倾斜角的定义:
当直线 l 与x轴相交时,我们取x轴作为基准,x轴正向与直线l 向上方向之间所成的角叫做直线的倾斜角
注意: (1)直线向上方向;
(2)x轴的正方向。
倾斜角α的范围为:
.
y
x
o
这样,在平面直角坐标系中,每一条直线都有一个确定的倾斜角,而且方向相同的直线,其倾斜程度相同,斜角相等;方向不同的直线,其倾斜程度不同,倾斜角不相等
探究?
我们把一条直线倾斜角 的正切叫做这条直线的斜率。斜率通常用k表示,即:
直线的斜率
2
3
2
o
2
-
y
x
直线的斜率
倾斜角α不是90°的直线都有斜率,并且倾斜角不同,直线的斜率也不同.因此,可以用斜率表示直线的倾斜程度.
我们把一条直线倾斜角 的正切叫做这条直线的斜率。斜率通常用k表示,即:
(1)若一条直线的倾斜角为90°,则这条直线与x轴垂直. ( )
(2)任何一条直线有且只有一个倾斜角和它对应. ( )
√
×
【诊断分析】 1.判断正误.(请在括号中打“√”或“×”)
(3)零向量可以作为直线的方向向量. ( )
√
(4)直线的倾斜角是锐角时,直线的斜率为正;直线的倾斜角是钝角时,
直线的斜率为负.
(5)直线的倾斜角越大,它的斜率也越大;反过来,直线的斜率越大,
它的倾斜角也越大.
(6)所有的直线都有倾斜角,但不是所有的直线都有斜率,
倾斜角是90°的直线不存在斜率. ( )
探究点一 直线的倾斜角问题
例1 (1)如图2-1-1(1)和(2),直线l1和l2的倾斜角分别是 ( )
A.140°,104° B.150°,104°
C.150°,106° D.130°,106°
D
(2)若过点P(1,1+a)和Q(3,2a)的直线的倾斜角α为钝角,求实数a的取值范围.
(3)已知直线l的倾斜角α=45°,且P1(2,y1),P2(x2,5),P3(3,1)是直线l上的三点,求x2,y1的值.
变式 (1)一条直线l与x轴相交,其向上的方向与x轴的负方向所成的角为α,则l的倾斜角为 ( )
A.α B.180°-α C.90°+α D.90°+α或90°-α
课 中 探 究
B
(2)直线l1⊥l2,若直线l1的倾斜角为α,直线l2的倾斜角为β(β>α),则下列说法正确的是 ( )
A.β-α=90° B.α+β=90°
C.α+β=180° D.β-α为锐角
A
(3) 已知直线l经过点A(0,1),B(sin α,0),求直线l的倾斜角θ的取值范围.
拓展 已知两点A(-3,4),B(3,2),过点P(1,0)的直线l与线段AB有公共点,则直线l的斜率k的取值范围是 ,直线l的倾斜角α的取值范围是 .
k≤-1或k≥1
45°≤α≤135°
探究点二 求直线的斜率问题
例2 (1)直线l过点A(1,2),且不过第四象限,则
直线l的斜率的取值范围是 ( )
A.[0,2] B.[0,1]
C. D.
A
(2)已知直线l1的方向向量为n=(2,1),直线l2的倾斜角是直线l1的倾斜角的2倍,求直线l2的斜率.
变式 (1)过点A(m2-n2,m2+n2)和点B(2mn-2n2,2mn)(m≠n)的直线的斜率是 .
1
(2)已知A(a,2),B(5,1),C(-4,2a)三点在同一条直线上,则a的值是 .
2或
拓展2 已知实数x,y满足y=x2-x+2(-1≤x≤1),试求的最大值和最小值.
拓展1 若点P(x,y)在以A(2,4),B(3,2)为端点的线段上,
求的最大值和最小值.
探究点三 直线的方向向量的应用
例3 (1)已知经过两点A(2,3),B(4,5)的直线的一个方向向量为(1,k),则k的值为 .
1
(2)已知直线l的一个方向向量为(2,4),则直线l的斜率为 .
2
1.已知直线l的斜率的绝对值等于,则直线l的倾斜角为( )
A.60° B.30° C.60°或120° D.30°或150°
课 堂 评 价
C
2.过两点A(1,),B(4,2)的直线的倾斜角为 ( )
A.30° B.60° C.120° D.150°
A
3.已知直线l的倾斜角为α-15°,则下列结论中正确的是 ( )
A.0°≤α<180° B.15°<α<180° C.15°≤α<180° D.15°≤α<195°
D
4.若经过A(m,3),B(1,2)两点的直线的一个方向向量为(-3,-3),则m等于 ( )
A.2 B.1 C.-1 D.-2
A
6.直线L的倾斜角是连接(3,-5),(0,-9)两点的直线的倾斜角的两倍,求直线L的斜率。
课 堂 评 价
5.求过点M(0,2)和N(2,3m2+12m+13)(m∈R)的直线l的斜率k的取值范围。解:由斜率公式得直线l的斜率知识小结
1、直线的倾斜角的定义
2、直线的斜率的定义
3、两点间斜率公式
当直线 l 与x轴相交时,
我们取x轴作为基准,
x轴正向与直线 l 向上
方向之间所成的角α
叫做直线 l 的倾斜角.
一条直线的倾斜角 的正切值叫做这条
直线的斜率.
1.倾斜角的定义解读
(1)倾斜角的定义含有三个条件:①直线向上的方向;②x轴正方向;③小于平角的非负角.
(2)倾斜角从“形”的方面直观地体现了直线对于x轴的倾斜程度.
(3)平面直角坐标系内每一条直线都有一个确定的倾斜角,且倾斜程度相同的直线倾斜角相等;倾斜程度不同的直线,其倾斜角不相等.直线与倾斜角是多对一的关系.
2.直线的倾斜角与斜率的关系
(1)直线都存在唯一的倾斜角,但并不是每条直线都存在斜率,倾斜角为90°的直线没有斜率.
(2)直线的倾斜角是一个角(图形),而斜率是一个实数值(数),斜率的绝对值越大,直线的倾斜角越接近90°.
(3)不同的倾斜角对应不同的斜率,因此,要确定一条不垂直于x轴的直线,只要知道直线上一个定点和它的斜率即可.
3.直线方向向量与斜率的关系
(1)当直线的斜率存在时,直线的方向向量与向量(1,k)共线.
(2)当直线的斜率不存在时,直线的方向向量与向量(0,1)共线.
