人教版2019选修一2.1.1 直线的倾斜角与斜率 课件(21张PPT)
文档属性
| 名称 | 人教版2019选修一2.1.1 直线的倾斜角与斜率 课件(21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-04 05:00:53 | ||
图片预览




文档简介
(共21张PPT)
黄河旭日圆
感悟历史 引出课题
在以往的几何学习中,我们常常通过直观感知、操作确认、思辨论证、度量计算等方法研究几何图形的形状、大小和位置关系,这种方法通常称为综合法,是欧氏几何的常用方法.
解析几何
研究对象:几何图形.
研究方法:坐标法.
2.1.1 直线的倾斜角与斜率
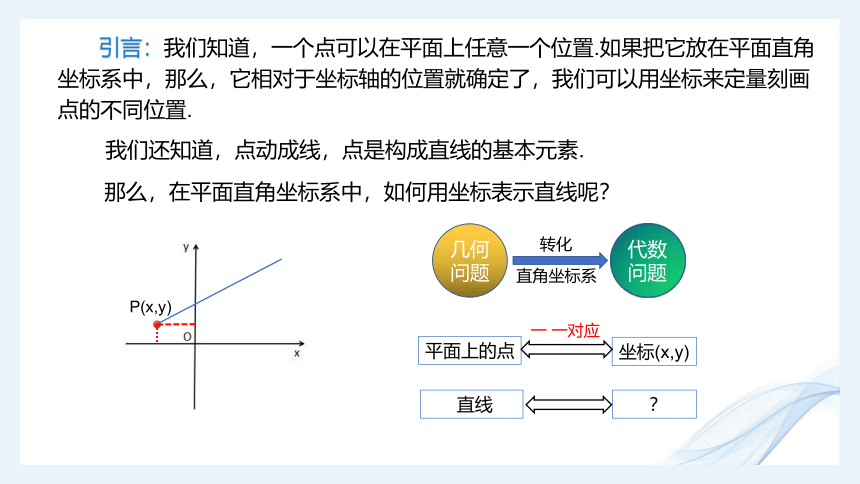
引言:我们知道,一个点可以在平面上任意一个位置.如果把它放在平面直角坐标系中,那么,它相对于坐标轴的位置就确定了,我们可以用坐标来定量刻画点的不同位置.
直线
?
几何问题
平面上的点
坐标(x,y)
代数问题
转化
直角坐标系
P(x,y)
一 一对应
我们还知道,点动成线,点是构成直线的基本元素.
那么,在平面直角坐标系中,如何用坐标表示直线呢?
自主探索 建构概念
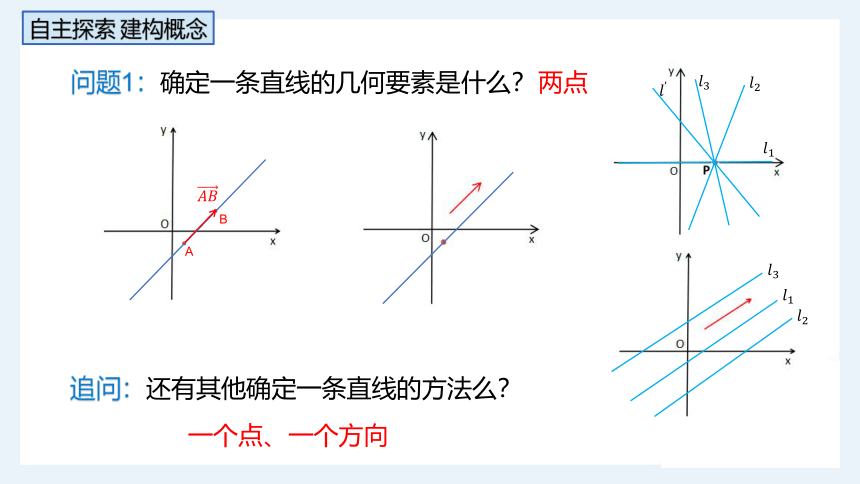
问题1:确定一条直线的几何要素是什么?
A
B
追问:还有其他确定一条直线的方法么?
两点
一个点、一个方向
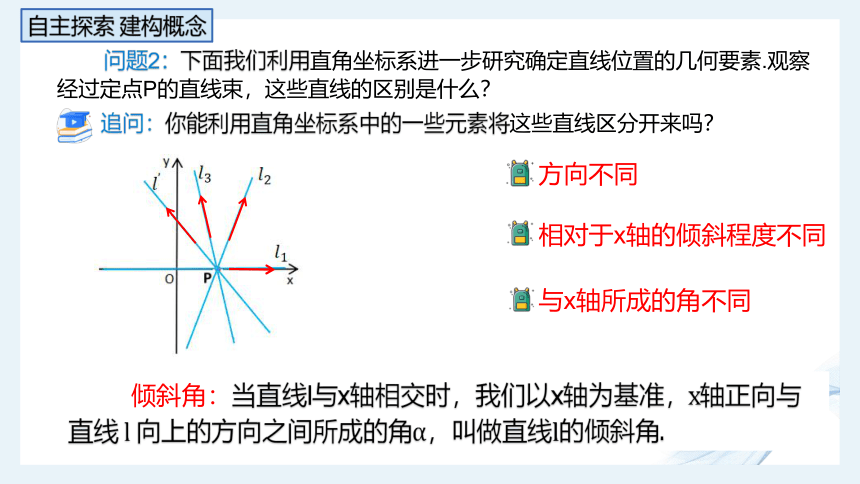
问题2:下面我们利用直角坐标系进一步研究确定直线位置的几何要素.观察经过定点P的直线束,这些直线的区别是什么?
自主探索 建构概念
方向不同
相对于x轴的倾斜程度不同
追问:你能利用直角坐标系中的一些元素将这些直线区分开来吗?
与x轴所成的角不同
倾斜角:当直线l与x轴相交时,我们以x轴为基准,x轴正向与直线 l 向上的方向之间所成的角α,叫做直线l的倾斜角.
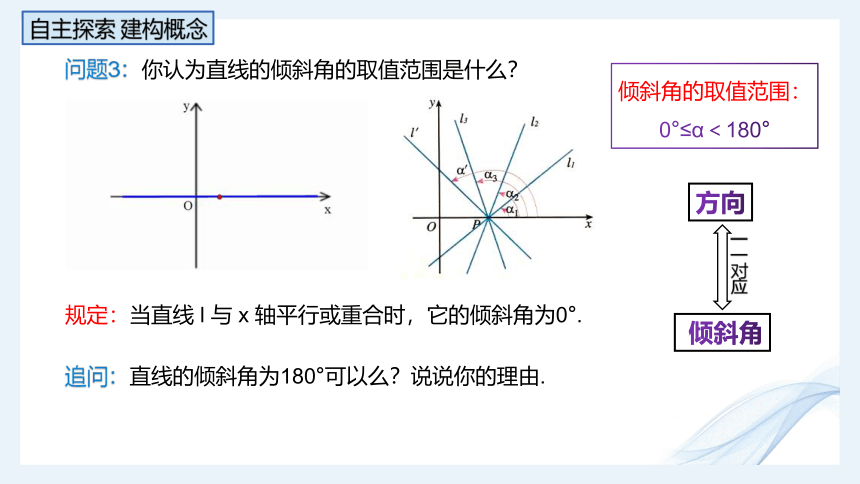
问题3:你认为直线的倾斜角的取值范围是什么?
自主探索 建构概念
规定:当直线 l 与 x 轴平行或重合时,它的倾斜角为0°.
追问:直线的倾斜角为180°可以么?说说你的理由.
倾斜角的取值范围:
0°≤α<180°
方向
倾斜角
一 一对应
自主探索 建构概念
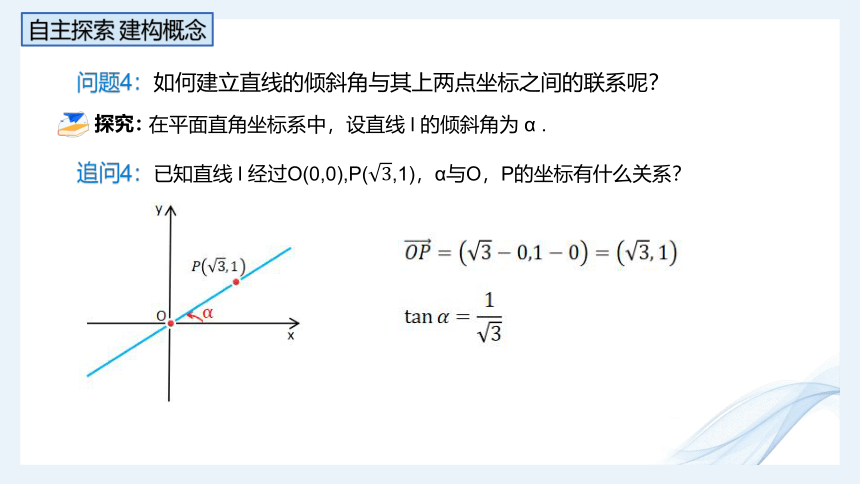
问题4:如何建立直线的倾斜角与其上两点坐标之间的联系呢?
追问2:两点如何表示直线的方向?
追问3:角如何与坐标建立关系?
下面我们一起来探究.
设P1(x1,y1),P2(x2,y2)(其中x1≠x2)是直线 l 上的两点,由两点确定一条直线可知,直线 l 由P1,P2唯一确定.可以推断,直线 l 的倾斜角一定与P1,P2两点的坐标有内在联系..
追问1:倾斜角定量刻画了直线的方向,两点确定一条直线也可以归结为一个点和一个方向确定一条直线,那倾斜角与两点坐标能以什么为桥梁建立关系呢?
自主探索 建构概念
探究:
在平面直角坐标系中,设直线 l 的倾斜角为 α .
问题4:如何建立直线的倾斜角与其上两点坐标之间的联系呢?
追问4:已知直线 l 经过O(0,0),P(,1),α与O,P的坐标有什么关系?
自主探索 建构概念
追问5:已知直线 l 经过P1(-1,1),P2(,0),α与P1,P2的坐标又有什么关系?
探究:
在平面直角坐标系中,设直线 l 的倾斜角为 α .
问题4:如何建立直线的倾斜角与其上两点坐标之间的联系呢?
P
α为锐角
自主探索 建构概念
追问6:一般地,如果直线 l 经过两点P1(x1,y1),P2(x2,y2)(其中x1≠x2),那么α与P1,P2的坐标有怎样的关系?
探究:
在平面直角坐标系中,设直线 l 的倾斜角为 α .
问题4:如何建立直线的倾斜角与其上两点坐标之间的联系呢?
P
P
α为钝角
自主探索 建构概念
追问6:一般地,如果直线 l 经过两点P1(x1,y1),P2(x2,y2)(其中x1≠x2),那么α与
P1,P2的坐标有怎样的关系?
探究:
在平面直角坐标系中,设直线 l 的倾斜角为 α .
问题4:如何建立直线的倾斜角与其上两点坐标之间的联系呢?
P
P
方向向上
α为锐角
α为钝角
自主探索 建构概念
追问7:当直线P1P2与x轴平行或重合时,上述式子还成立吗?为什么?
问题4:如何建立直线的倾斜角与其上两点坐标之间的联系呢?
当直线的倾斜角α为锐角或钝角时,满足:
直线 l 的倾斜角α与直线 l 上两点P1(x1,y1),P2(x2,y2)(其中x1≠x2)的坐标有如下关系:
自主探索 建构概念
我们把一条直线的倾斜角的正切值叫做这条直线的斜率.斜率通常用k表示,即
追问:当直线的倾斜角由0°逐渐增大到180°时,
其斜率如何变化?为什么?
倾斜角
斜率
除90°外
一 一对应
自主探索 建构概念
(2)当直线与y轴平行或重合时,上述式子还适用吗?为什么?
(1)已知直线上的两点A(a1,a2),B(b1,b2),运用上述公式计算直线AB的斜率时,与A,B两点的顺序有关吗?
问题7:由
和
可以得到经过两点P1(x1,y1),P2(x2,y2)(x1≠x2)
的直线的斜率公式为:
自主探索 建构概念
问题8:我们知道,直线上的向量以及与它平行的非零向量都是直线的方向向量.
你能发现直
线的方向向量与斜率 k 之间的关系吗?
当直线的斜率为,它的一个方向向量的坐标为时,
学以致用 解决问题
例1 如图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
O
x
y
A
C
B
1 2 3 4
-4 -3 -2 -1
3
2
1
-1
-2
小结提升 布置作业
问题9: 请同学们回顾“刻画直线几何特征的完整过程”,体会“解析几何研究几何图形的基本过程”,感悟其中的数学思想和方法.
对确定直线位置的几何要素的刻画:
类比、分类讨论、转化与化归、数形结合思想
形
数
坐标法
感悟历史 引出课题
研究对象:点、直线、圆等几何图形.
研究方法:坐标法.
解析几何
基本内涵和方法:
几何问题
代数结果
代数问题
转化
运
算
翻
译
形
数
小结提升 布置作业
今日作业
教科书习题2.1第1,2,3,4,7,8题.
自主探索 建构概念
形
数
斜率
除90°外
一 一对应
方向
倾斜角
一 一对应
直线的方向
坐标法
黄河旭日圆
感悟历史 引出课题
在以往的几何学习中,我们常常通过直观感知、操作确认、思辨论证、度量计算等方法研究几何图形的形状、大小和位置关系,这种方法通常称为综合法,是欧氏几何的常用方法.
解析几何
研究对象:几何图形.
研究方法:坐标法.
2.1.1 直线的倾斜角与斜率
引言:我们知道,一个点可以在平面上任意一个位置.如果把它放在平面直角坐标系中,那么,它相对于坐标轴的位置就确定了,我们可以用坐标来定量刻画点的不同位置.
直线
?
几何问题
平面上的点
坐标(x,y)
代数问题
转化
直角坐标系
P(x,y)
一 一对应
我们还知道,点动成线,点是构成直线的基本元素.
那么,在平面直角坐标系中,如何用坐标表示直线呢?
自主探索 建构概念
问题1:确定一条直线的几何要素是什么?
A
B
追问:还有其他确定一条直线的方法么?
两点
一个点、一个方向
问题2:下面我们利用直角坐标系进一步研究确定直线位置的几何要素.观察经过定点P的直线束,这些直线的区别是什么?
自主探索 建构概念
方向不同
相对于x轴的倾斜程度不同
追问:你能利用直角坐标系中的一些元素将这些直线区分开来吗?
与x轴所成的角不同
倾斜角:当直线l与x轴相交时,我们以x轴为基准,x轴正向与直线 l 向上的方向之间所成的角α,叫做直线l的倾斜角.
问题3:你认为直线的倾斜角的取值范围是什么?
自主探索 建构概念
规定:当直线 l 与 x 轴平行或重合时,它的倾斜角为0°.
追问:直线的倾斜角为180°可以么?说说你的理由.
倾斜角的取值范围:
0°≤α<180°
方向
倾斜角
一 一对应
自主探索 建构概念
问题4:如何建立直线的倾斜角与其上两点坐标之间的联系呢?
追问2:两点如何表示直线的方向?
追问3:角如何与坐标建立关系?
下面我们一起来探究.
设P1(x1,y1),P2(x2,y2)(其中x1≠x2)是直线 l 上的两点,由两点确定一条直线可知,直线 l 由P1,P2唯一确定.可以推断,直线 l 的倾斜角一定与P1,P2两点的坐标有内在联系..
追问1:倾斜角定量刻画了直线的方向,两点确定一条直线也可以归结为一个点和一个方向确定一条直线,那倾斜角与两点坐标能以什么为桥梁建立关系呢?
自主探索 建构概念
探究:
在平面直角坐标系中,设直线 l 的倾斜角为 α .
问题4:如何建立直线的倾斜角与其上两点坐标之间的联系呢?
追问4:已知直线 l 经过O(0,0),P(,1),α与O,P的坐标有什么关系?
自主探索 建构概念
追问5:已知直线 l 经过P1(-1,1),P2(,0),α与P1,P2的坐标又有什么关系?
探究:
在平面直角坐标系中,设直线 l 的倾斜角为 α .
问题4:如何建立直线的倾斜角与其上两点坐标之间的联系呢?
P
α为锐角
自主探索 建构概念
追问6:一般地,如果直线 l 经过两点P1(x1,y1),P2(x2,y2)(其中x1≠x2),那么α与P1,P2的坐标有怎样的关系?
探究:
在平面直角坐标系中,设直线 l 的倾斜角为 α .
问题4:如何建立直线的倾斜角与其上两点坐标之间的联系呢?
P
P
α为钝角
自主探索 建构概念
追问6:一般地,如果直线 l 经过两点P1(x1,y1),P2(x2,y2)(其中x1≠x2),那么α与
P1,P2的坐标有怎样的关系?
探究:
在平面直角坐标系中,设直线 l 的倾斜角为 α .
问题4:如何建立直线的倾斜角与其上两点坐标之间的联系呢?
P
P
方向向上
α为锐角
α为钝角
自主探索 建构概念
追问7:当直线P1P2与x轴平行或重合时,上述式子还成立吗?为什么?
问题4:如何建立直线的倾斜角与其上两点坐标之间的联系呢?
当直线的倾斜角α为锐角或钝角时,满足:
直线 l 的倾斜角α与直线 l 上两点P1(x1,y1),P2(x2,y2)(其中x1≠x2)的坐标有如下关系:
自主探索 建构概念
我们把一条直线的倾斜角的正切值叫做这条直线的斜率.斜率通常用k表示,即
追问:当直线的倾斜角由0°逐渐增大到180°时,
其斜率如何变化?为什么?
倾斜角
斜率
除90°外
一 一对应
自主探索 建构概念
(2)当直线与y轴平行或重合时,上述式子还适用吗?为什么?
(1)已知直线上的两点A(a1,a2),B(b1,b2),运用上述公式计算直线AB的斜率时,与A,B两点的顺序有关吗?
问题7:由
和
可以得到经过两点P1(x1,y1),P2(x2,y2)(x1≠x2)
的直线的斜率公式为:
自主探索 建构概念
问题8:我们知道,直线上的向量以及与它平行的非零向量都是直线的方向向量.
你能发现直
线的方向向量与斜率 k 之间的关系吗?
当直线的斜率为,它的一个方向向量的坐标为时,
学以致用 解决问题
例1 如图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
O
x
y
A
C
B
1 2 3 4
-4 -3 -2 -1
3
2
1
-1
-2
小结提升 布置作业
问题9: 请同学们回顾“刻画直线几何特征的完整过程”,体会“解析几何研究几何图形的基本过程”,感悟其中的数学思想和方法.
对确定直线位置的几何要素的刻画:
类比、分类讨论、转化与化归、数形结合思想
形
数
坐标法
感悟历史 引出课题
研究对象:点、直线、圆等几何图形.
研究方法:坐标法.
解析几何
基本内涵和方法:
几何问题
代数结果
代数问题
转化
运
算
翻
译
形
数
小结提升 布置作业
今日作业
教科书习题2.1第1,2,3,4,7,8题.
自主探索 建构概念
形
数
斜率
除90°外
一 一对应
方向
倾斜角
一 一对应
直线的方向
坐标法
