第十三章 轴对称单元总结及练习(含答案)
图片预览



文档简介
中小学教育资源及组卷应用平台
轴对称
知识点一 轴对称图形
1、轴对称图形:如果一个图形沿某一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴。
2、轴对称:有一个图形沿着某一条直线折叠, 如果它能够与另一个图形重合,那么就说这两个图形关于这条直线(成轴)对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点。
3、图形轴对称的性质
(1)如果两个图形成轴对称,那么对称轴是任何一对对应点所连线段的垂直平分线
(2)轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线.
4、画一图形关于某条直线的轴对称图形的步骤:找到关键点,画出关键点的对应点,按照原图顺序依次连接各点。
5、轴对称与轴对称图形的区别
(1)轴对称是指两个图形之间的形状与位置关系,
(2)成轴对称的两个图形是全等形,轴对称图形是一个具有特殊形状的图形,
(3)把一个轴对称图形沿对称轴分成两个图形,这两个图形是全等形,并且成轴对称。
知识点二 线段的垂直平分线
1、定义:经过线段的中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线(或线段的中垂线).
2、性质:线段的垂直平分线上的点与这条线段两个端点的距离相等。
3、判定:与一条线段两个端点距离相等的点在这条线段的垂直平分线上。
练习:
如图,有A,B,C三个村庄,现准备要建一所希望小学,要求学校到三个村庄的距离相等,请你确定学校的位置.
如图,AB=AC=8cm,AB的垂直平分线交AC于D,若△ADB的周长为18,求DC的长
3.如图,△ABC中DE⊥AB,AD平分∠BCA,DE⊥AB于E,求证:直线AD是CE的垂直平分线。
知识点三 轴对称变换及用坐标表示轴对称
1、轴对称变换的性质
(1)经过轴对称变换得到的图形与原图形的形状、大小完全一样
(2)经过轴对称变换得到的图形上的每一点都是原图形上的某一点关于对称轴的对称点.
(3)连接任意一对对应点的线段被对称轴垂直平分.
2、作一个图形关于某条直线的轴对称图形
(1)作出一些关键点或特殊点的对称点.
(2)按原图形的连接方式连接所得到的对称点,即得到原图形的轴对称图形.
3、关于坐标轴对称
点P (x,y)关于x轴对称的点的坐标是(x,-y)
点P (x,y)关于y轴对称的点的坐标是(-x,y)
扩展:
(1)点P(x,y)关于原点对称的点的坐标是(-x,-y)
(2)点P (x,y)关于第一、三象限坐标轴夹角平分线y=x对称的点的坐标是(y, x)
点P (x, y)关于第二、四象限坐标轴夹角平分线y=-x 对称的点的坐标是(-y,- x)
(3)点P (x, y)关于直线x=m对称的点的坐标是(2m-x,y);
点P (x,y)关于直线y=n对称的点的坐标是(x, 2n-y);
练习:
1.平面直角坐标系内的点A(-1,2)与点B(-1,-2)关于( )
A.y轴对称 B.x轴对称 C.原点对称 D.直线y=x对称
2.在平面直角坐标系中,将点A(-1,2)向右平移3个单位长度得到点B,则点B关于x轴的对称点C的坐标是( )
A.(-4,-2) B.(2,2) C.(-2,2) D.(2,-2)
3.设点M(x,y)在第二象限,且|x|=2,|y|=3,则点M关于y轴的对称点的坐标是( )
A.(2,3) B.(-2,3) C.(-3,2) D.(-3,-2)
4.若|a-2|+(b-5)2=0,则点P (a,b)关于x轴对称的点的坐标为 .
5.已知△ABC的三个顶点的坐标分别为A(-3,5),B(- 4,1),
C(-1,3),作出△ABC关于y轴对称的图形
知识点四 特殊三角形
等腰三角形
1、定义:有两条边相等的三角形是等腰三角形。相等的两条边叫做腰,另一条边叫做底边,两腰所夹的角叫做顶角,腰与底边的夹角叫做底角。
2、性质:(1)等腰三角形的两个底角相等(简写成“等边对等角”)
(2)等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(三线合一)
注意:(选择题可直接使用)
等腰三角形两腰上的中线、角平分线、高线对应相等.
3、判定
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
注意:(选择题可直接使用)
(1)有一边上的角平分线、中线、高线互相重合的三角形是等腰三角形.
(2)有两边上的角平分线对应相等的: :角形是等腰三角形.
(3)有两边上的中线对应相等的三角形是等腰三角形.
(4)有两边上的高线对应相等的三角形是等腰三角形.
二、等边三角形
1、定义:三条边都相等的三角形叫做等边三角形,也叫做正三角形
2、性质:等边三角形的三个内角都相等,并且每一个内角都等于60°
3、判定:(1)三条边都相等的三角形是等边三角形;
(2)三个角都相等的三角形是等边三角形;
(3)有一个角是60°的等腰三角形是等边三角形。
三、直角三角形
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
扩展:性质:直角三角形斜边上的中线等于斜边的一半
判定:如果一个三角形一边上的中线等于这边上的一半,那么,这个三角形是直角三角形,该边为斜边。
练习:
1.如图,在△ABC中,BA=BC,∠B=120°,AB的垂直平分线交AC于D,求证:AD=
2.如图所示,在等边△ABC中,AE=CD,AD、BE相交于点P,BQ⊥AD于点Q,求证:BP=2PQ
3.如图,△ABC是等边三角形,E是AC上一点,D是BC延长线上一点,连接BE,DE,若∠ABE=40°,BE=DE,求∠CED的度数
变式训练:如图,△ABC是等边三角形,BD平分∠ABC,延长BC到E,使得CE=CD.求证:BD=DE.
知识点五 最短路径问题
1、原理:两点之间线段最短、垂线段最短、三角形三边关系、轴对称、平移
2、解题思路:找对称点,实现“折线”变“直线”。
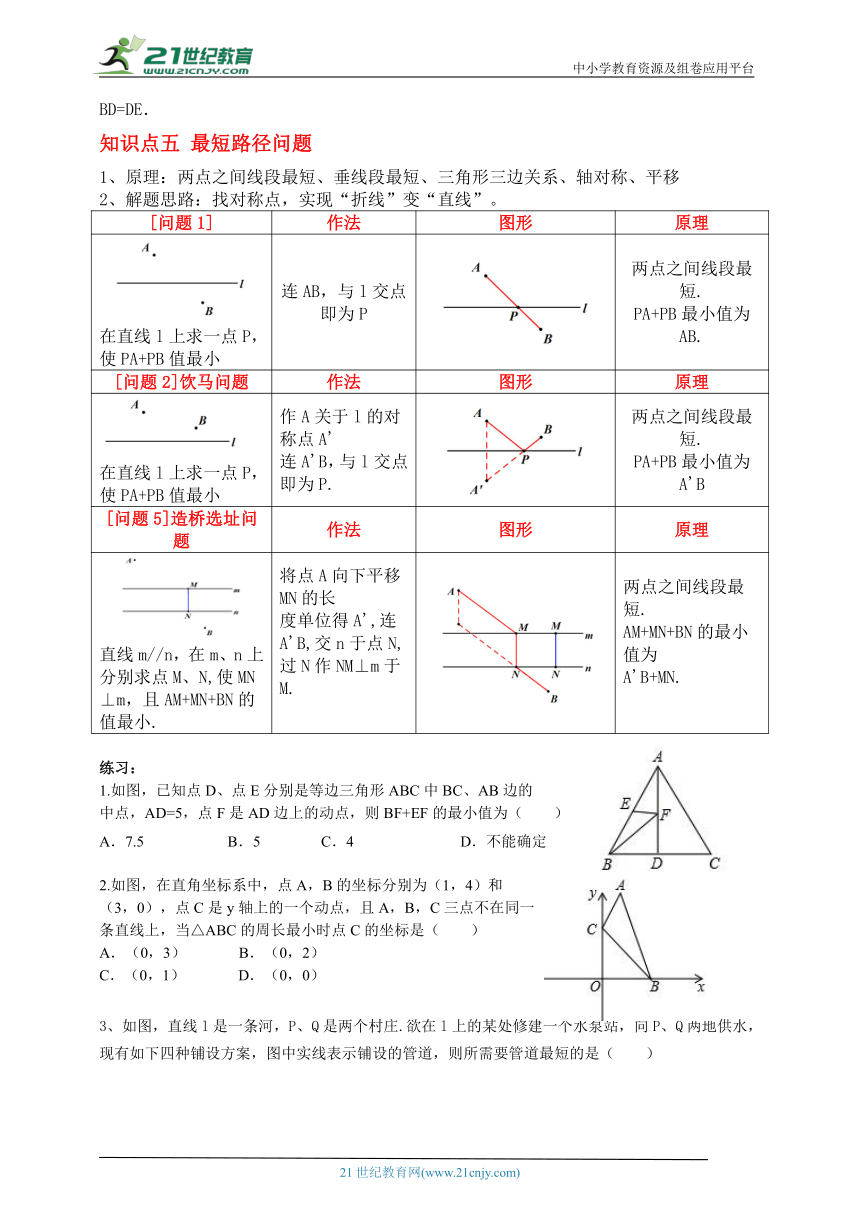
[问题1] 作法 图形 原理
在直线l上求一点P,使PA+PB值最小 连AB,与l交点即为P 两点之间线段最短.PA+PB最小值为AB.
[问题2]饮马问题 作法 图形 原理
在直线l上求一点P,使PA+PB值最小 作A关于l的对称点A'连A'B,与l交点即为P. 两点之间线段最短.PA+PB最小值为A'B
[问题5]造桥选址问题 作法 图形 原理
直线m//n,在m、n上分别求点M、N,使MN⊥m,且AM+MN+BN的值最小. 将点A向下平移MN的长度单位得A',连A'B,交n于点N,过N作NM⊥m于M. 两点之间线段最短.AM+MN+BN的最小值为A'B+MN.
练习:
1.如图,已知点D、点E分别是等边三角形ABC中BC、AB边的
中点,AD=5,点F是AD边上的动点,则BF+EF的最小值为( )
A.7.5 B.5 C.4 D.不能确定
2.如图,在直角坐标系中,点A,B的坐标分别为(1,4)和
(3,0),点C是y轴上的一个动点,且A,B,C三点不在同一
条直线上,当△ABC的周长最小时点C的坐标是( )
A.(0,3) B.(0,2)
C.(0,1) D.(0,0)
3、如图,直线l是一条河,P、Q是两个村庄.欲在l上的某处修建一个水泵站,向P、Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需要管道最短的是( )
4.如图,一个旅游船从大桥AB 的P 处前往山脚下的Q 处接游客,
然后将游客送往河岸BC 上,再返回P 处,请画出旅游船的最短路径.
答案:
知识点二 线段的垂直平分线
解:学校在连接任意两点的两条线段的垂直平分线的交点处
2.解:∵DM是AB的垂直平分线
∴AD=BD
设CD的长为X,则AD=AC-CD=8-X
∵C△ADB=AB+AD+BD=8+(8-X)+(8-X)=18
∴X=3
即CD的长为3cm.
3.证明:∵AD平分∠BCA,DE⊥AB, DE⊥AB
∴DE=CD
∴点D在CE的垂直平分线上,
在RT△AED与RT△ACD中
∵AD=AD,DE=DC
∴RT△AED≌RT△ACD
∴AE=AC
∴点A在CE的垂直平分线上
直线AD是CE的垂直平分线。
知识点三 轴对称变换及用坐标表示轴对称
B 2.D 3.A 4.(2.-5)
5.解:点A(-3,5),B(-4,1),C(-1,3),关于y轴的对称点分别为A′(3,5),B′(4,1),C′(1,3).依次连接A′B′,B′C′,C′A′,就得到△ABC关于y轴对称的△A′B′C′.
知识点四 特殊三角形
1.证明:连接BD
∵BA=BC,∠B=120°
∴∠A=∠C=30°
∵DE是AB的垂直平分线
∴DA=DB
∴∠ABD=∠A=30°
∵∠CBD=∠ABC-∠ABC=120°-30°=90°
又∵∠C=30°
∴DB=1/2CD
∴AD=1/2CD
2.证明:∵△ABC是等边三角形
∴∠BAE=∠C=60°,AB=AC
∵在△ABE与△CAD中
∴△ABE≌△CAD
∴∠ABE=∠CAD
∵∠BPQ=∠BAP+∠ABE=∠BAP+∠CAD=∠BAC=60°
∵BQ⊥AD
∴∠PBQ=30°
∴BP=2PQ
3.解:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵∠ABE=40°,
∴∠EBC=∠ABC-∠ABE=60°-40°=20°.
∵BE=DE,
∴∠D=∠EBC=20°,
∴∠CED=∠ACB-∠D=40°
变式训练:证明:∵△ABC是等边三角形,BD是角平分线,
∴∠ABC=∠ACB=60°,∠DBC=30°.
又∵CE=CD,
∴∠CDE=∠CED.
又∵∠BCD=∠CDE+∠CED,
∴∠CDE=∠CED=30°.
∴∠DBC=∠DEC.
∴DB=DE(等角对等边)
知识点五 最短路径问题
B 2.A 3.D
4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
轴对称
知识点一 轴对称图形
1、轴对称图形:如果一个图形沿某一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴。
2、轴对称:有一个图形沿着某一条直线折叠, 如果它能够与另一个图形重合,那么就说这两个图形关于这条直线(成轴)对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点。
3、图形轴对称的性质
(1)如果两个图形成轴对称,那么对称轴是任何一对对应点所连线段的垂直平分线
(2)轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线.
4、画一图形关于某条直线的轴对称图形的步骤:找到关键点,画出关键点的对应点,按照原图顺序依次连接各点。
5、轴对称与轴对称图形的区别
(1)轴对称是指两个图形之间的形状与位置关系,
(2)成轴对称的两个图形是全等形,轴对称图形是一个具有特殊形状的图形,
(3)把一个轴对称图形沿对称轴分成两个图形,这两个图形是全等形,并且成轴对称。
知识点二 线段的垂直平分线
1、定义:经过线段的中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线(或线段的中垂线).
2、性质:线段的垂直平分线上的点与这条线段两个端点的距离相等。
3、判定:与一条线段两个端点距离相等的点在这条线段的垂直平分线上。
练习:
如图,有A,B,C三个村庄,现准备要建一所希望小学,要求学校到三个村庄的距离相等,请你确定学校的位置.
如图,AB=AC=8cm,AB的垂直平分线交AC于D,若△ADB的周长为18,求DC的长
3.如图,△ABC中DE⊥AB,AD平分∠BCA,DE⊥AB于E,求证:直线AD是CE的垂直平分线。
知识点三 轴对称变换及用坐标表示轴对称
1、轴对称变换的性质
(1)经过轴对称变换得到的图形与原图形的形状、大小完全一样
(2)经过轴对称变换得到的图形上的每一点都是原图形上的某一点关于对称轴的对称点.
(3)连接任意一对对应点的线段被对称轴垂直平分.
2、作一个图形关于某条直线的轴对称图形
(1)作出一些关键点或特殊点的对称点.
(2)按原图形的连接方式连接所得到的对称点,即得到原图形的轴对称图形.
3、关于坐标轴对称
点P (x,y)关于x轴对称的点的坐标是(x,-y)
点P (x,y)关于y轴对称的点的坐标是(-x,y)
扩展:
(1)点P(x,y)关于原点对称的点的坐标是(-x,-y)
(2)点P (x,y)关于第一、三象限坐标轴夹角平分线y=x对称的点的坐标是(y, x)
点P (x, y)关于第二、四象限坐标轴夹角平分线y=-x 对称的点的坐标是(-y,- x)
(3)点P (x, y)关于直线x=m对称的点的坐标是(2m-x,y);
点P (x,y)关于直线y=n对称的点的坐标是(x, 2n-y);
练习:
1.平面直角坐标系内的点A(-1,2)与点B(-1,-2)关于( )
A.y轴对称 B.x轴对称 C.原点对称 D.直线y=x对称
2.在平面直角坐标系中,将点A(-1,2)向右平移3个单位长度得到点B,则点B关于x轴的对称点C的坐标是( )
A.(-4,-2) B.(2,2) C.(-2,2) D.(2,-2)
3.设点M(x,y)在第二象限,且|x|=2,|y|=3,则点M关于y轴的对称点的坐标是( )
A.(2,3) B.(-2,3) C.(-3,2) D.(-3,-2)
4.若|a-2|+(b-5)2=0,则点P (a,b)关于x轴对称的点的坐标为 .
5.已知△ABC的三个顶点的坐标分别为A(-3,5),B(- 4,1),
C(-1,3),作出△ABC关于y轴对称的图形
知识点四 特殊三角形
等腰三角形
1、定义:有两条边相等的三角形是等腰三角形。相等的两条边叫做腰,另一条边叫做底边,两腰所夹的角叫做顶角,腰与底边的夹角叫做底角。
2、性质:(1)等腰三角形的两个底角相等(简写成“等边对等角”)
(2)等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(三线合一)
注意:(选择题可直接使用)
等腰三角形两腰上的中线、角平分线、高线对应相等.
3、判定
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
注意:(选择题可直接使用)
(1)有一边上的角平分线、中线、高线互相重合的三角形是等腰三角形.
(2)有两边上的角平分线对应相等的: :角形是等腰三角形.
(3)有两边上的中线对应相等的三角形是等腰三角形.
(4)有两边上的高线对应相等的三角形是等腰三角形.
二、等边三角形
1、定义:三条边都相等的三角形叫做等边三角形,也叫做正三角形
2、性质:等边三角形的三个内角都相等,并且每一个内角都等于60°
3、判定:(1)三条边都相等的三角形是等边三角形;
(2)三个角都相等的三角形是等边三角形;
(3)有一个角是60°的等腰三角形是等边三角形。
三、直角三角形
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
扩展:性质:直角三角形斜边上的中线等于斜边的一半
判定:如果一个三角形一边上的中线等于这边上的一半,那么,这个三角形是直角三角形,该边为斜边。
练习:
1.如图,在△ABC中,BA=BC,∠B=120°,AB的垂直平分线交AC于D,求证:AD=
2.如图所示,在等边△ABC中,AE=CD,AD、BE相交于点P,BQ⊥AD于点Q,求证:BP=2PQ
3.如图,△ABC是等边三角形,E是AC上一点,D是BC延长线上一点,连接BE,DE,若∠ABE=40°,BE=DE,求∠CED的度数
变式训练:如图,△ABC是等边三角形,BD平分∠ABC,延长BC到E,使得CE=CD.求证:BD=DE.
知识点五 最短路径问题
1、原理:两点之间线段最短、垂线段最短、三角形三边关系、轴对称、平移
2、解题思路:找对称点,实现“折线”变“直线”。
[问题1] 作法 图形 原理
在直线l上求一点P,使PA+PB值最小 连AB,与l交点即为P 两点之间线段最短.PA+PB最小值为AB.
[问题2]饮马问题 作法 图形 原理
在直线l上求一点P,使PA+PB值最小 作A关于l的对称点A'连A'B,与l交点即为P. 两点之间线段最短.PA+PB最小值为A'B
[问题5]造桥选址问题 作法 图形 原理
直线m//n,在m、n上分别求点M、N,使MN⊥m,且AM+MN+BN的值最小. 将点A向下平移MN的长度单位得A',连A'B,交n于点N,过N作NM⊥m于M. 两点之间线段最短.AM+MN+BN的最小值为A'B+MN.
练习:
1.如图,已知点D、点E分别是等边三角形ABC中BC、AB边的
中点,AD=5,点F是AD边上的动点,则BF+EF的最小值为( )
A.7.5 B.5 C.4 D.不能确定
2.如图,在直角坐标系中,点A,B的坐标分别为(1,4)和
(3,0),点C是y轴上的一个动点,且A,B,C三点不在同一
条直线上,当△ABC的周长最小时点C的坐标是( )
A.(0,3) B.(0,2)
C.(0,1) D.(0,0)
3、如图,直线l是一条河,P、Q是两个村庄.欲在l上的某处修建一个水泵站,向P、Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需要管道最短的是( )
4.如图,一个旅游船从大桥AB 的P 处前往山脚下的Q 处接游客,
然后将游客送往河岸BC 上,再返回P 处,请画出旅游船的最短路径.
答案:
知识点二 线段的垂直平分线
解:学校在连接任意两点的两条线段的垂直平分线的交点处
2.解:∵DM是AB的垂直平分线
∴AD=BD
设CD的长为X,则AD=AC-CD=8-X
∵C△ADB=AB+AD+BD=8+(8-X)+(8-X)=18
∴X=3
即CD的长为3cm.
3.证明:∵AD平分∠BCA,DE⊥AB, DE⊥AB
∴DE=CD
∴点D在CE的垂直平分线上,
在RT△AED与RT△ACD中
∵AD=AD,DE=DC
∴RT△AED≌RT△ACD
∴AE=AC
∴点A在CE的垂直平分线上
直线AD是CE的垂直平分线。
知识点三 轴对称变换及用坐标表示轴对称
B 2.D 3.A 4.(2.-5)
5.解:点A(-3,5),B(-4,1),C(-1,3),关于y轴的对称点分别为A′(3,5),B′(4,1),C′(1,3).依次连接A′B′,B′C′,C′A′,就得到△ABC关于y轴对称的△A′B′C′.
知识点四 特殊三角形
1.证明:连接BD
∵BA=BC,∠B=120°
∴∠A=∠C=30°
∵DE是AB的垂直平分线
∴DA=DB
∴∠ABD=∠A=30°
∵∠CBD=∠ABC-∠ABC=120°-30°=90°
又∵∠C=30°
∴DB=1/2CD
∴AD=1/2CD
2.证明:∵△ABC是等边三角形
∴∠BAE=∠C=60°,AB=AC
∵在△ABE与△CAD中
∴△ABE≌△CAD
∴∠ABE=∠CAD
∵∠BPQ=∠BAP+∠ABE=∠BAP+∠CAD=∠BAC=60°
∵BQ⊥AD
∴∠PBQ=30°
∴BP=2PQ
3.解:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵∠ABE=40°,
∴∠EBC=∠ABC-∠ABE=60°-40°=20°.
∵BE=DE,
∴∠D=∠EBC=20°,
∴∠CED=∠ACB-∠D=40°
变式训练:证明:∵△ABC是等边三角形,BD是角平分线,
∴∠ABC=∠ACB=60°,∠DBC=30°.
又∵CE=CD,
∴∠CDE=∠CED.
又∵∠BCD=∠CDE+∠CED,
∴∠CDE=∠CED=30°.
∴∠DBC=∠DEC.
∴DB=DE(等角对等边)
知识点五 最短路径问题
B 2.A 3.D
4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
