15.2.3整数指数幂(2) 课件(18张ppt)
文档属性
| 名称 | 15.2.3整数指数幂(2) 课件(18张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-03 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
15.2.3整数指数幂(2)
人教版八年级上册
教学目标
【知识与技能】
1.会利用10的负整数次幂,用科学记数法表示一些绝对值较小的数.
2.经历探索用10的负整数次幂来表示绝对值较小的数的过程,完善科学记数法,培养正向、逆向思维能力.
【过程与方法】
经历探索用科学记数法表示数的过程,理解科学记数法.
【情感、态度与价值观】
用科学记数法的形式渗透数学的简洁之美,通过完善科学记数法,培养对数学完美形式的追求.
新知导入
1、用科学计数法表示下列各数。
我国的人口大约为1 300 000 000人
太阳的半径为696 000 000千米
光的速度为300 000 000米/秒
2、思考:对于一个很小的数如0.000 098 2可以用科学计数法表示吗?该怎么表示?
新知讲解
用科学记数法表示绝对值小于1的小数
知识点
0.1=
0.01=
0.001= = ;
0.000 1= = ;
0.000 01= = .
探究:
新知讲解
思考:
如何用科学记数法表示0.003 5和0.000 098 2呢?
归纳:
新知讲解
0.000 098 2=9.82×0.000 01=9.82×
0.003 5=3.5×0.001 =3.5×
规律:
对于一个小于1的正小数,从小数点前的第一个0算起至小数点后第一个非0数字前有几个0,用科学记数法表示这个数时,10的指数就是负几.
观察上面两个等式,10的指数与什么有关呢?
新知探究
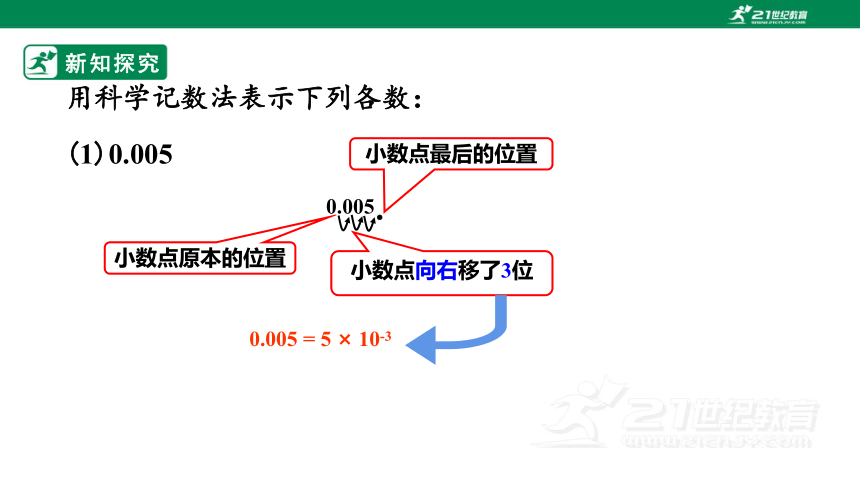
(1)0.005
0.005
0.005 = 5 × 10-3
小数点原本的位置
小数点最后的位置
小数点向右移了3位
用科学记数法表示下列各数:
新知探究
(2)0.0204
0.02 04
0.0204=2.04×10-2
小数点原本的位置
小数点最后的位置
小数点向右移了2位
例题讲解
解:(1)0.3=3×10-1 ;
(2)-0.000 78=-7.8×10-4 ;
(3)0.000 020 09=2.009×10-5.
例1 用科学记数法表示下列各数:
(1)0.3; (2)-0.000 78;
(3)0.000 020 09.
强化练习
1.用科学记数法表示下列数:
0. 000 000 001 , 0. 001 2, 0. 000 000 345, 0. 000 000 010 8.
【课本P145 下方练习 第1题】
强化练习
2.下列是用科学记数法表示的数,试写出它的原数.
(1)4.5×10-8= ;
(2)-3.14×10-6= ;
(3)3.05×10-3= .
0.000000045
-0.00000314
-0.00305
例题讲解
解:1 mm =10-3 m,1 nm =10-9 m.
答:1 nm3 的空间可以放1018个1 nm3 的物体.
例2 纳米(nm)是非常小的长度单位,1 nm =
10-9 m.把1 nm3 的物体放到乒乓球上,就如同把乒乓球放到地球上.1 mm3 的空间可以放多少个1 nm3 的物体(物体之间的间隙忽略不计)?
方法总结:科学记数法的有关计算,分别把前边的数进行运算,10的幂进行运算,再把所得结果相乘.
强化练习
3.计算:
(1)(2×10-6) ×(3.2×103); (2)(2×10-6)2÷(10-4) 3 .
【课本P146 练习 第2题】
课堂总结
用科学记数法表示绝对值小于1的小数规律:
对于一个小于1的正小数,从小数点前的第一个0算起至小数点后第一个非0数字前有几个0,用科学记数法表示这个数时,10的指数就是负几.
拓展提高
1、目前世界上能制造的芯片最小工艺水平是5纳米,而我国能制造芯片的最小工艺水平是16纳米,已知1纳米=10﹣9米,用科学记数法将16纳米表示为 _____________米.
1.6×10﹣8
拓展提高
2、一根约为1米长、直径为80毫米的光纤预制棒,可拉成至少400公里长的光纤.试问:1平方厘米是这种光纤的横截面积的多少倍?(用科学记数法表示且保留一位小数)
解:这种光纤的横截面积为
1÷(1.256×10-4)≈8.0×103
答:1平方厘米是这种光纤的横截面的8.0×103倍.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
15.2.3整数指数幂(2)
人教版八年级上册
教学目标
【知识与技能】
1.会利用10的负整数次幂,用科学记数法表示一些绝对值较小的数.
2.经历探索用10的负整数次幂来表示绝对值较小的数的过程,完善科学记数法,培养正向、逆向思维能力.
【过程与方法】
经历探索用科学记数法表示数的过程,理解科学记数法.
【情感、态度与价值观】
用科学记数法的形式渗透数学的简洁之美,通过完善科学记数法,培养对数学完美形式的追求.
新知导入
1、用科学计数法表示下列各数。
我国的人口大约为1 300 000 000人
太阳的半径为696 000 000千米
光的速度为300 000 000米/秒
2、思考:对于一个很小的数如0.000 098 2可以用科学计数法表示吗?该怎么表示?
新知讲解
用科学记数法表示绝对值小于1的小数
知识点
0.1=
0.01=
0.001= = ;
0.000 1= = ;
0.000 01= = .
探究:
新知讲解
思考:
如何用科学记数法表示0.003 5和0.000 098 2呢?
归纳:
新知讲解
0.000 098 2=9.82×0.000 01=9.82×
0.003 5=3.5×0.001 =3.5×
规律:
对于一个小于1的正小数,从小数点前的第一个0算起至小数点后第一个非0数字前有几个0,用科学记数法表示这个数时,10的指数就是负几.
观察上面两个等式,10的指数与什么有关呢?
新知探究
(1)0.005
0.005
0.005 = 5 × 10-3
小数点原本的位置
小数点最后的位置
小数点向右移了3位
用科学记数法表示下列各数:
新知探究
(2)0.0204
0.02 04
0.0204=2.04×10-2
小数点原本的位置
小数点最后的位置
小数点向右移了2位
例题讲解
解:(1)0.3=3×10-1 ;
(2)-0.000 78=-7.8×10-4 ;
(3)0.000 020 09=2.009×10-5.
例1 用科学记数法表示下列各数:
(1)0.3; (2)-0.000 78;
(3)0.000 020 09.
强化练习
1.用科学记数法表示下列数:
0. 000 000 001 , 0. 001 2, 0. 000 000 345, 0. 000 000 010 8.
【课本P145 下方练习 第1题】
强化练习
2.下列是用科学记数法表示的数,试写出它的原数.
(1)4.5×10-8= ;
(2)-3.14×10-6= ;
(3)3.05×10-3= .
0.000000045
-0.00000314
-0.00305
例题讲解
解:1 mm =10-3 m,1 nm =10-9 m.
答:1 nm3 的空间可以放1018个1 nm3 的物体.
例2 纳米(nm)是非常小的长度单位,1 nm =
10-9 m.把1 nm3 的物体放到乒乓球上,就如同把乒乓球放到地球上.1 mm3 的空间可以放多少个1 nm3 的物体(物体之间的间隙忽略不计)?
方法总结:科学记数法的有关计算,分别把前边的数进行运算,10的幂进行运算,再把所得结果相乘.
强化练习
3.计算:
(1)(2×10-6) ×(3.2×103); (2)(2×10-6)2÷(10-4) 3 .
【课本P146 练习 第2题】
课堂总结
用科学记数法表示绝对值小于1的小数规律:
对于一个小于1的正小数,从小数点前的第一个0算起至小数点后第一个非0数字前有几个0,用科学记数法表示这个数时,10的指数就是负几.
拓展提高
1、目前世界上能制造的芯片最小工艺水平是5纳米,而我国能制造芯片的最小工艺水平是16纳米,已知1纳米=10﹣9米,用科学记数法将16纳米表示为 _____________米.
1.6×10﹣8
拓展提高
2、一根约为1米长、直径为80毫米的光纤预制棒,可拉成至少400公里长的光纤.试问:1平方厘米是这种光纤的横截面积的多少倍?(用科学记数法表示且保留一位小数)
解:这种光纤的横截面积为
1÷(1.256×10-4)≈8.0×103
答:1平方厘米是这种光纤的横截面的8.0×103倍.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
