5.5 实际问题与方程(一)(课件)-五年级上册数学 人教版 (共14张PPT)
文档属性
| 名称 | 5.5 实际问题与方程(一)(课件)-五年级上册数学 人教版 (共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-03 17:36:57 | ||
图片预览





文档简介
(共14张PPT)
人教版数学五年级上册
5.5 实际问题与方程(一)
小川原来的跳高成绩是1.05米,现在达到了1.12米。成绩提高了多少米?
1.
1.12-1.05 = 0.07(米)
用方程表示下面的数量关系。
2.
(1)x与5.6的和等于12。
(2)x的3倍再加上26等于50。
x + 5.6 = 12
3x + 26 = 50
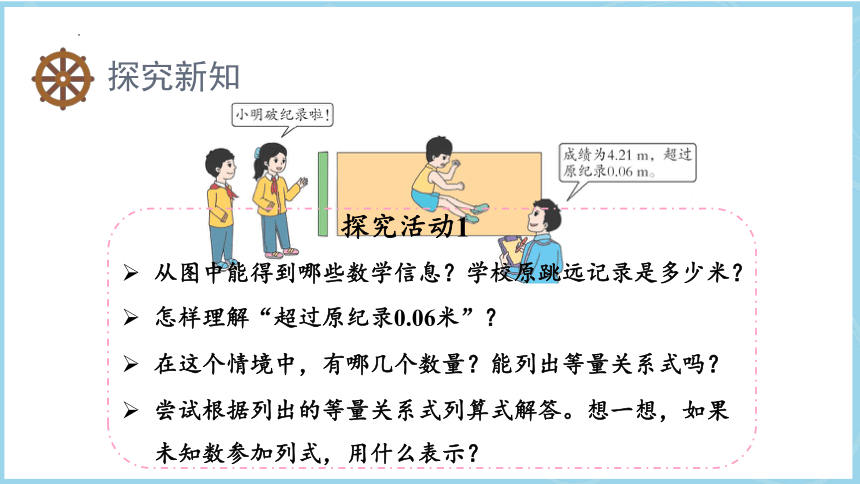
从图中能得到哪些数学信息?学校原跳远记录是多少米?
怎样理解“超过原纪录0.06米”?
在这个情境中,有哪几个数量?能列出等量关系式吗?
探究活动1
尝试根据列出的等量关系式列算式解答。想一想,如果未知数参加列式,用什么表示?
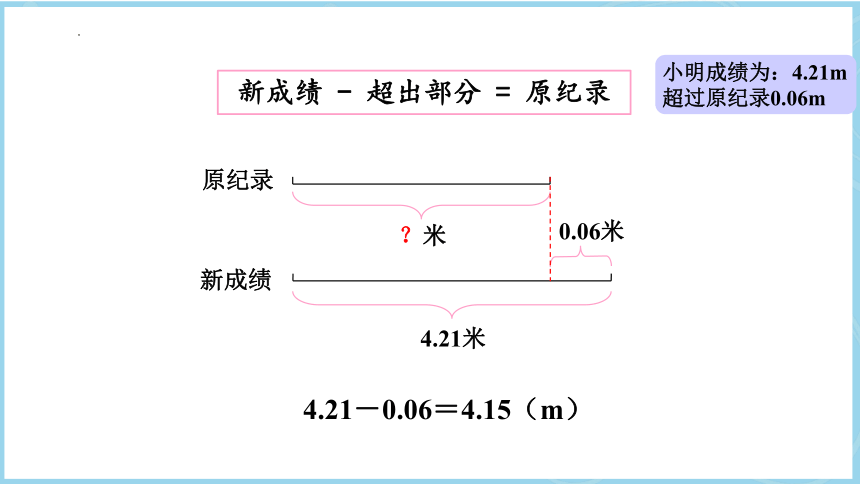
新成绩 - 超出部分 = 原纪录
原纪录 + 超出部分 = 新成绩
新成绩 – 原纪录 = 超出部分
4.21米
0.06米
?米
原纪录
新成绩
4.21-0.06=4.15(m)
新成绩 - 超出部分 = 原纪录
小明成绩为:4.21m
超过原纪录0.06m
原纪录 + 超出部分 = 新成绩
解:设学校原跳远纪录是x米。
x = 4.15
x + 0.06-0.06 = 4.21-0.06
x + 0.06 = 4.21
小明成绩为:4.21m
超过原纪录0.06m
新成绩 – 原纪录 = 超出部分
解:设学校原跳远纪录是x米。
4.21-x = 0.06
4.21-x+x = 0.06+x
4.21= 0.06+x
0.06+x = 4.21
0.06+x-0.06 = 4.21-0.06
x = 4.15
小明成绩为:4.21m
超过原纪录0.06m
新成绩 – 原纪录 = 超出部分
解:设学校原跳远纪录是x米。
4.21-x = 0.06
4.21-x+x = 0.06+x
4.21= 0.06+x
0.06+x = 4.21
0.06+x-0.06 = 4.21-0.06
x = 4.15
所以,x = 4.15是方程的解。
=方程右边
= 0.06
= 4.21-4.15
方程左边 = 4.21-x
检验:
用方程的思路解决问题,你认为关键是什么?
同一个问题,我们用了几种不同的方法解决?都合理吗?
可以用算术的方法,也可以列方程解答。
找出等量关系
方程解法与算术解法有什么区别
列方程解决问题时,未知数用字母表示,参与列式;
算术方法中未知数不参与列式。
探究活动2
解:设小明去年身高x米。
0.08+x=1.53
0.08+x-x=1.53-x
x=1.45
8cm=0.08m
答:小明去年身高1.45米。
解法一:
1.小明今年的身高是1.53m,比去年长高了8cm。小明去年身高多少米?
8cm=0.08m
解法二:
解:设小明去年身高x米。
1.53-x=0.08
1.53-x+x=0.08+x
1.53=0.08+x
0.08+x=1.53
0.08+x-0.08=1.53-0.08
x=1.45
1.小明今年的身高是1.53m,比去年长高了8cm。小明去年身高多少米?
2.
每分钟滴的水×30=半小时滴的水
x=0.06
答:一个滴水的水龙头每分钟浪费0.06千克水。
30x=1.8
30x÷30=1.8÷30
解:设一个滴水的水龙头每分钟浪费x千克水。
半小时=30分
解:设一个滴水的水龙头每分钟浪费x千克水。
半小时=30分
半小时滴的水÷每分钟滴的水=30
1.8=30x
答:一个滴水的水龙头每分钟浪费0.06千克水。
1.8÷x=30
1.8÷x×x=30×x
x=0.06
30x=1.8
30x÷30=1.8÷30
2.
启发思考
轮流展示
灵活运用
对比分析
人教版数学五年级上册
5.5 实际问题与方程(一)
小川原来的跳高成绩是1.05米,现在达到了1.12米。成绩提高了多少米?
1.
1.12-1.05 = 0.07(米)
用方程表示下面的数量关系。
2.
(1)x与5.6的和等于12。
(2)x的3倍再加上26等于50。
x + 5.6 = 12
3x + 26 = 50
从图中能得到哪些数学信息?学校原跳远记录是多少米?
怎样理解“超过原纪录0.06米”?
在这个情境中,有哪几个数量?能列出等量关系式吗?
探究活动1
尝试根据列出的等量关系式列算式解答。想一想,如果未知数参加列式,用什么表示?
新成绩 - 超出部分 = 原纪录
原纪录 + 超出部分 = 新成绩
新成绩 – 原纪录 = 超出部分
4.21米
0.06米
?米
原纪录
新成绩
4.21-0.06=4.15(m)
新成绩 - 超出部分 = 原纪录
小明成绩为:4.21m
超过原纪录0.06m
原纪录 + 超出部分 = 新成绩
解:设学校原跳远纪录是x米。
x = 4.15
x + 0.06-0.06 = 4.21-0.06
x + 0.06 = 4.21
小明成绩为:4.21m
超过原纪录0.06m
新成绩 – 原纪录 = 超出部分
解:设学校原跳远纪录是x米。
4.21-x = 0.06
4.21-x+x = 0.06+x
4.21= 0.06+x
0.06+x = 4.21
0.06+x-0.06 = 4.21-0.06
x = 4.15
小明成绩为:4.21m
超过原纪录0.06m
新成绩 – 原纪录 = 超出部分
解:设学校原跳远纪录是x米。
4.21-x = 0.06
4.21-x+x = 0.06+x
4.21= 0.06+x
0.06+x = 4.21
0.06+x-0.06 = 4.21-0.06
x = 4.15
所以,x = 4.15是方程的解。
=方程右边
= 0.06
= 4.21-4.15
方程左边 = 4.21-x
检验:
用方程的思路解决问题,你认为关键是什么?
同一个问题,我们用了几种不同的方法解决?都合理吗?
可以用算术的方法,也可以列方程解答。
找出等量关系
方程解法与算术解法有什么区别
列方程解决问题时,未知数用字母表示,参与列式;
算术方法中未知数不参与列式。
探究活动2
解:设小明去年身高x米。
0.08+x=1.53
0.08+x-x=1.53-x
x=1.45
8cm=0.08m
答:小明去年身高1.45米。
解法一:
1.小明今年的身高是1.53m,比去年长高了8cm。小明去年身高多少米?
8cm=0.08m
解法二:
解:设小明去年身高x米。
1.53-x=0.08
1.53-x+x=0.08+x
1.53=0.08+x
0.08+x=1.53
0.08+x-0.08=1.53-0.08
x=1.45
1.小明今年的身高是1.53m,比去年长高了8cm。小明去年身高多少米?
2.
每分钟滴的水×30=半小时滴的水
x=0.06
答:一个滴水的水龙头每分钟浪费0.06千克水。
30x=1.8
30x÷30=1.8÷30
解:设一个滴水的水龙头每分钟浪费x千克水。
半小时=30分
解:设一个滴水的水龙头每分钟浪费x千克水。
半小时=30分
半小时滴的水÷每分钟滴的水=30
1.8=30x
答:一个滴水的水龙头每分钟浪费0.06千克水。
1.8÷x=30
1.8÷x×x=30×x
x=0.06
30x=1.8
30x÷30=1.8÷30
2.
启发思考
轮流展示
灵活运用
对比分析
