人教版八年级上册13.3.1 等腰三角形的性质 课件(共18张PPT)
文档属性
| 名称 | 人教版八年级上册13.3.1 等腰三角形的性质 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-03 19:13:06 | ||
图片预览





文档简介
(共18张PPT)
等腰三角形的性质
从生活中来
看一看
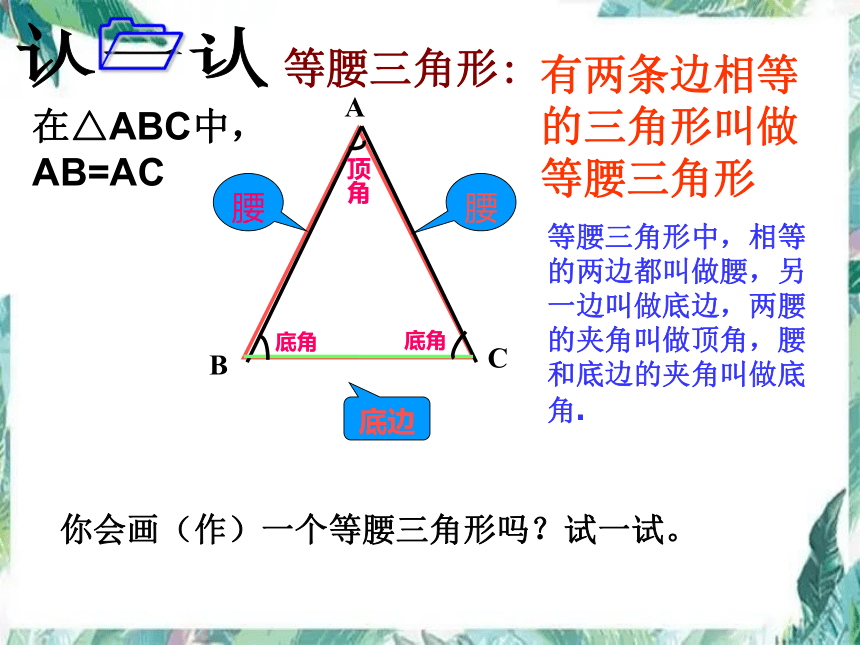
你会画(作)一个等腰三角形吗?试一试。
等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
A
C
B
腰
腰
底边
顶角
底角
底角
在△ABC中, AB=AC
等腰三角形:
有两条边相等的三角形叫做等腰三角形
如图,把一张长方形的纸按图中虚线对折,
并剪去绿色部分,
再把它展开,得到的△ABC是等腰三角形吗 说说理由.
A
B
C
D
A
B
C
A
B
C
D
(B)
把剪出的等腰三角形ABC沿折痕对折,观察说明:等腰三角形是轴对称图形吗?为什么?
折叠后还有哪些线段重叠、哪些角重叠?
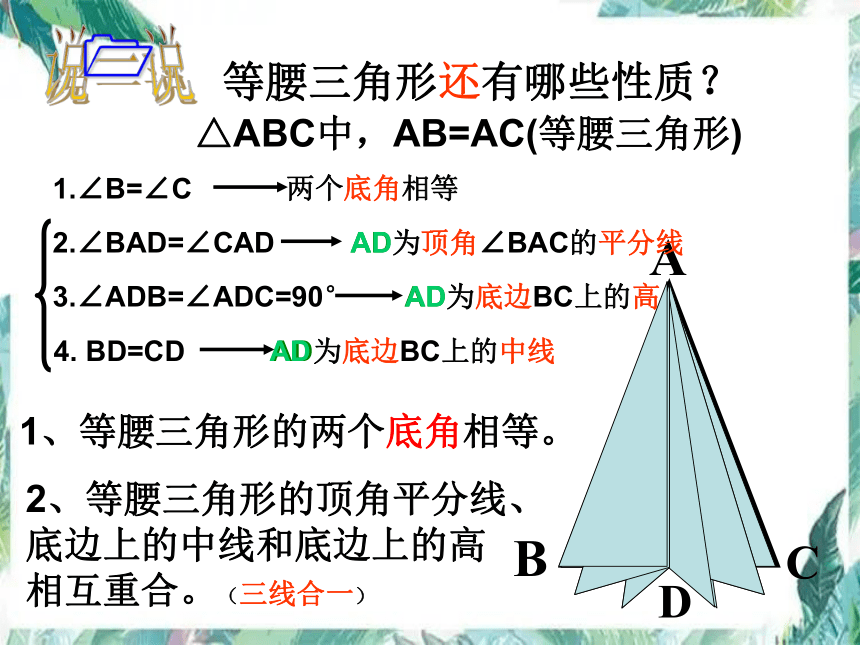
你认为等腰三角形还有哪些性质?说一说你的看法。
B
D
A
B
C
等腰三角形还有哪些性质?
△ABC中,AB=AC(等腰三角形)
1.∠B=∠C
两个底角相等
2.∠BAD=∠CAD
AD为顶角∠BAC的平分线
3.∠ADB=∠ADC=90°
AD为底边BC上的高
4. BD=CD
AD为底边BC上的中线
AD
AD
AD
1、等腰三角形的两个底角相等。
2、等腰三角形的顶角平分线、底边上的中线和底边上的高 相互重合。(三线合一)
A
B
C
等腰三角形的两个底角相等。
己知: △ABC中,AB=AC
求证: ∠B = ∠C
作底边BC边上的中线AD
在△ABD和△ACD中
AB=AC
BD=CD
AD=AD
∴△ABD≌△ACD(SSS)
∴∠B = ∠C
用法: 在 △ABC中
∵ AB=AC
∴ ∠ B= ∠ C
(等 边对等 角)
(等边对等角)
证 明:
D
受性质1证明的启发,你能证明性质2等腰三角形顶角平分线、底边上的中线、底边上的高相互重合吗
(三线合一)
A
C
D
B
2.把上面的命题写成
如果…那么…的形式
1.上面的命题还有不同的
描述方法吗
A
B
C
在△ABD和△ACD中
AB=AC
BD=CD
AD=AD
∴△ABD≌△ACD(SSS)
证明:
D
∴ ∠ BAD= ∠ CAD
∴ AD为顶角平分线
∴ ∠ ADB= ∠ ADC=900
∴ AD为底边上的高
己知: △ABC中,AB=AC,
求证:
AD为 顶角的 平分线
AD为 底边上的高
AD为 底边上的中线
AD为 底边上的高
AD为 顶角的 平分线
AD为 底边上的中线
AD为 底边上的 中线
AD为 顶角的 平分线
AD为 底边上的 高
(等 边 对 等 角 )的应用
500、500或200、800
350、350
练一练
1.填空
(1)在一个等腰三角形中, 顶角为 800, 其余两角为 _______。
(2)在一个等腰三角形中, 一角为 800 , 其余两角为 ______________。 (3)在一个等腰三角形中, 一角为 1100, 其余两个角为_______。
500、500
练一练
2. 填空
(1)在一个等腰三角形中, 有两边为 5和 6 , 则它的周长为 _______。
(2)在一个等腰三角形中, 有两边为 5和12 , 则它的周长为 _______。
3.已知:如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD, 求△ABC各角的度数.
练一练
1)图中共有几个等腰三角形
2)共有几个角,这些角有关系吗 说说理由.
3) ,若∠A=x0,这些角都能用x表示吗 能求出这些角吗?
x0
x0
x0
2x0
2x0
到生活中去
1 如图,某厂房屋顶钢架外框是等腰三角形,其中 AB=AC,立柱AD⊥BC,且顶角∠BAC=100 °,根据己知条件求出下列角的度数,并说明理由。
B
C
A
D
B
C
A
D
2.∠BAD和∠CAD
1.∠B 和 ∠C
闯一闯
拓展提高
2.四川地震过后,北川中学的同学用下面的方法检测教室的房梁是否水平 :在等腰直角三角尺的斜边中点拴一条线绳,线绳的另一端挂一个铅锤,把这个直角三角形的斜边贴在房梁上, 结果线绳经过直角三角尺的直角顶点, 他们确信房梁是水平的,他们的作法有道理吗?
B
C
D
A
理一理
1.本节课你学习了哪些知识?
2.到目前为止,说明两个角相等的方法有哪些?
3.本节课所运用的学习方法对今后学习有什么启示?
巩固应用:
1、教科书P56 习题12.3 1,3,7题
2、请问:在等腰三角形中,等腰三角形两腰上 的中线(高线)是否相等?为什么?
3、在生活中发现可以利用等腰三角形的性质解决的问题。
这节课你有哪些收获
1.判断正误:
(1).如图,∵AD=AE
∴ ∠ 1= ∠ 2
(等边对等角)( )
A
B
C
D
E
1
2
(2).如图 ,∵AB=BC
∴ ∠ B= ∠ C
(等边对等角)( )
A
B
C
(等边对等角)的应用
练一练
等腰三角形的性质
从生活中来
看一看
你会画(作)一个等腰三角形吗?试一试。
等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
A
C
B
腰
腰
底边
顶角
底角
底角
在△ABC中, AB=AC
等腰三角形:
有两条边相等的三角形叫做等腰三角形
如图,把一张长方形的纸按图中虚线对折,
并剪去绿色部分,
再把它展开,得到的△ABC是等腰三角形吗 说说理由.
A
B
C
D
A
B
C
A
B
C
D
(B)
把剪出的等腰三角形ABC沿折痕对折,观察说明:等腰三角形是轴对称图形吗?为什么?
折叠后还有哪些线段重叠、哪些角重叠?
你认为等腰三角形还有哪些性质?说一说你的看法。
B
D
A
B
C
等腰三角形还有哪些性质?
△ABC中,AB=AC(等腰三角形)
1.∠B=∠C
两个底角相等
2.∠BAD=∠CAD
AD为顶角∠BAC的平分线
3.∠ADB=∠ADC=90°
AD为底边BC上的高
4. BD=CD
AD为底边BC上的中线
AD
AD
AD
1、等腰三角形的两个底角相等。
2、等腰三角形的顶角平分线、底边上的中线和底边上的高 相互重合。(三线合一)
A
B
C
等腰三角形的两个底角相等。
己知: △ABC中,AB=AC
求证: ∠B = ∠C
作底边BC边上的中线AD
在△ABD和△ACD中
AB=AC
BD=CD
AD=AD
∴△ABD≌△ACD(SSS)
∴∠B = ∠C
用法: 在 △ABC中
∵ AB=AC
∴ ∠ B= ∠ C
(等 边对等 角)
(等边对等角)
证 明:
D
受性质1证明的启发,你能证明性质2等腰三角形顶角平分线、底边上的中线、底边上的高相互重合吗
(三线合一)
A
C
D
B
2.把上面的命题写成
如果…那么…的形式
1.上面的命题还有不同的
描述方法吗
A
B
C
在△ABD和△ACD中
AB=AC
BD=CD
AD=AD
∴△ABD≌△ACD(SSS)
证明:
D
∴ ∠ BAD= ∠ CAD
∴ AD为顶角平分线
∴ ∠ ADB= ∠ ADC=900
∴ AD为底边上的高
己知: △ABC中,AB=AC,
求证:
AD为 顶角的 平分线
AD为 底边上的高
AD为 底边上的中线
AD为 底边上的高
AD为 顶角的 平分线
AD为 底边上的中线
AD为 底边上的 中线
AD为 顶角的 平分线
AD为 底边上的 高
(等 边 对 等 角 )的应用
500、500或200、800
350、350
练一练
1.填空
(1)在一个等腰三角形中, 顶角为 800, 其余两角为 _______。
(2)在一个等腰三角形中, 一角为 800 , 其余两角为 ______________。 (3)在一个等腰三角形中, 一角为 1100, 其余两个角为_______。
500、500
练一练
2. 填空
(1)在一个等腰三角形中, 有两边为 5和 6 , 则它的周长为 _______。
(2)在一个等腰三角形中, 有两边为 5和12 , 则它的周长为 _______。
3.已知:如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD, 求△ABC各角的度数.
练一练
1)图中共有几个等腰三角形
2)共有几个角,这些角有关系吗 说说理由.
3) ,若∠A=x0,这些角都能用x表示吗 能求出这些角吗?
x0
x0
x0
2x0
2x0
到生活中去
1 如图,某厂房屋顶钢架外框是等腰三角形,其中 AB=AC,立柱AD⊥BC,且顶角∠BAC=100 °,根据己知条件求出下列角的度数,并说明理由。
B
C
A
D
B
C
A
D
2.∠BAD和∠CAD
1.∠B 和 ∠C
闯一闯
拓展提高
2.四川地震过后,北川中学的同学用下面的方法检测教室的房梁是否水平 :在等腰直角三角尺的斜边中点拴一条线绳,线绳的另一端挂一个铅锤,把这个直角三角形的斜边贴在房梁上, 结果线绳经过直角三角尺的直角顶点, 他们确信房梁是水平的,他们的作法有道理吗?
B
C
D
A
理一理
1.本节课你学习了哪些知识?
2.到目前为止,说明两个角相等的方法有哪些?
3.本节课所运用的学习方法对今后学习有什么启示?
巩固应用:
1、教科书P56 习题12.3 1,3,7题
2、请问:在等腰三角形中,等腰三角形两腰上 的中线(高线)是否相等?为什么?
3、在生活中发现可以利用等腰三角形的性质解决的问题。
这节课你有哪些收获
1.判断正误:
(1).如图,∵AD=AE
∴ ∠ 1= ∠ 2
(等边对等角)( )
A
B
C
D
E
1
2
(2).如图 ,∵AB=BC
∴ ∠ B= ∠ C
(等边对等角)( )
A
B
C
(等边对等角)的应用
练一练
