八年级上册 13.3.1 等腰三角形的性质 优质课件(共24张PPT)
文档属性
| 名称 | 八年级上册 13.3.1 等腰三角形的性质 优质课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 925.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-03 19:50:12 | ||
图片预览



文档简介
(共24张PPT)
课题:等腰三角形的性质
1、掌握等腰三角形的性质1;
2、能运用等腰三角形的性质1解决相关问题.
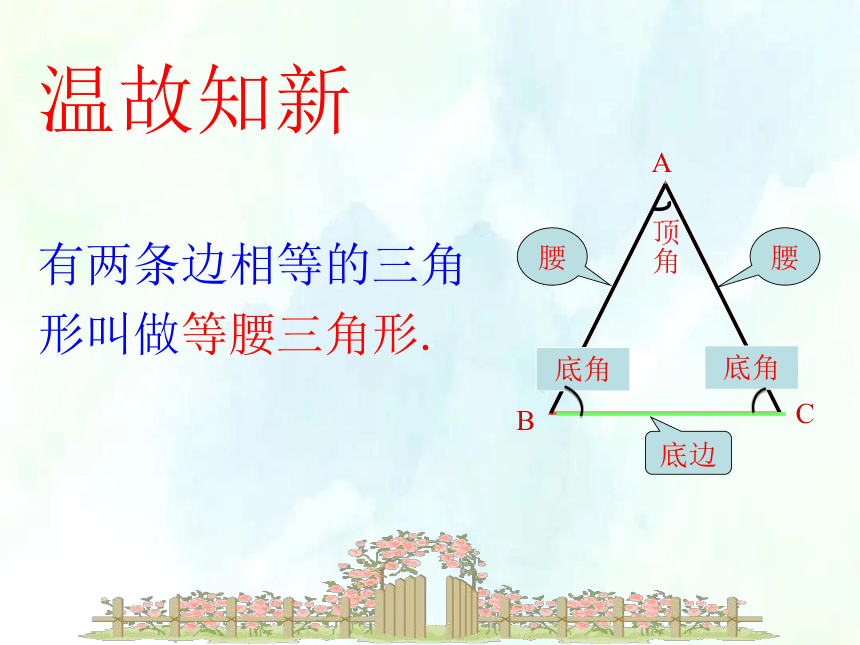
有两条边相等的三角形叫做等腰三角形.
A
C
B
腰
腰
底边
底角
底角
温故知新
顶角
拿出课前剪好的三角形纸片 !
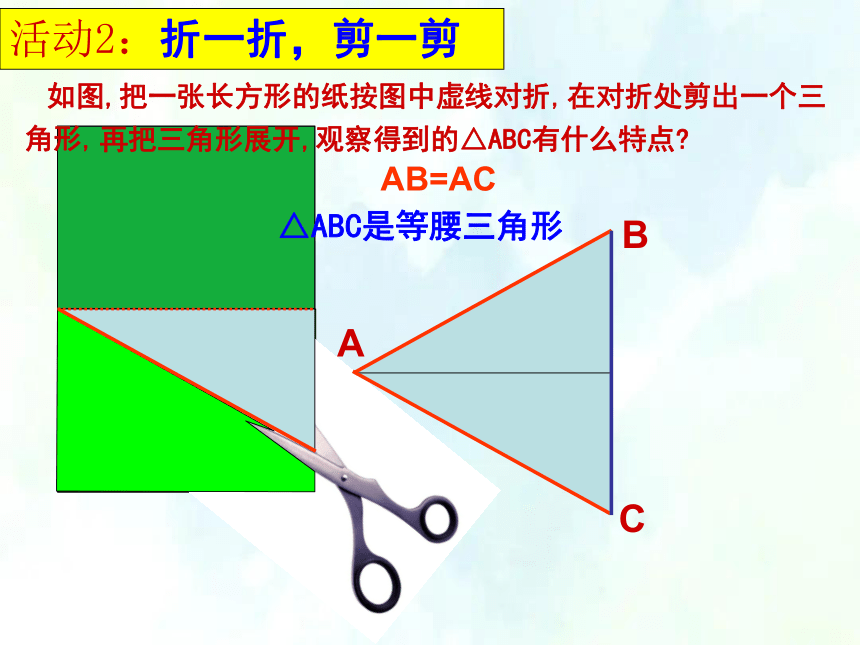
如图,把一张长方形的纸按图中虚线对折,
在对折处剪出一个三
再把三角形展开,观察得到的△ABC有什么特点
A
B
C
AB=AC
活动2:折一折,剪一剪
角形,
△ABC是等腰三角形
A
B
C
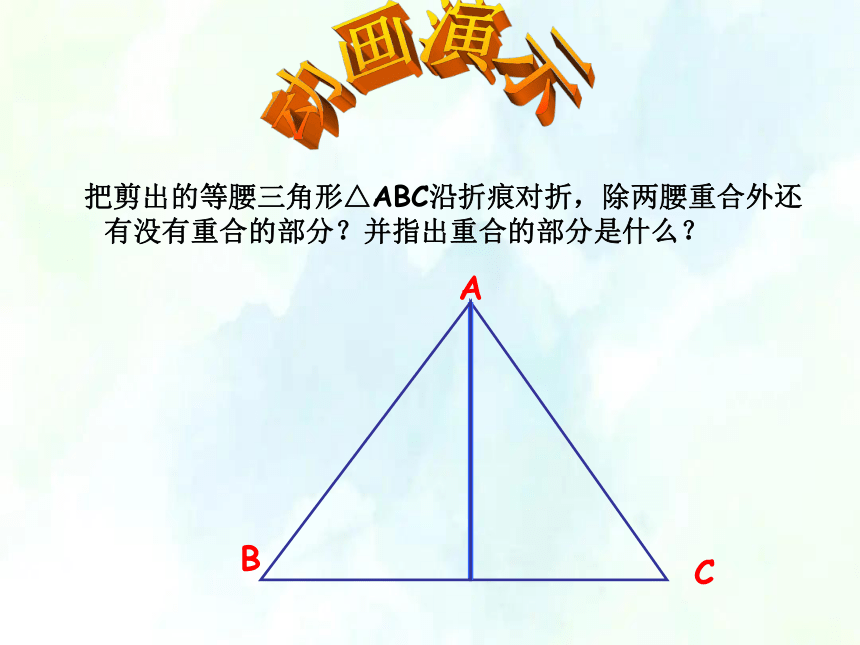
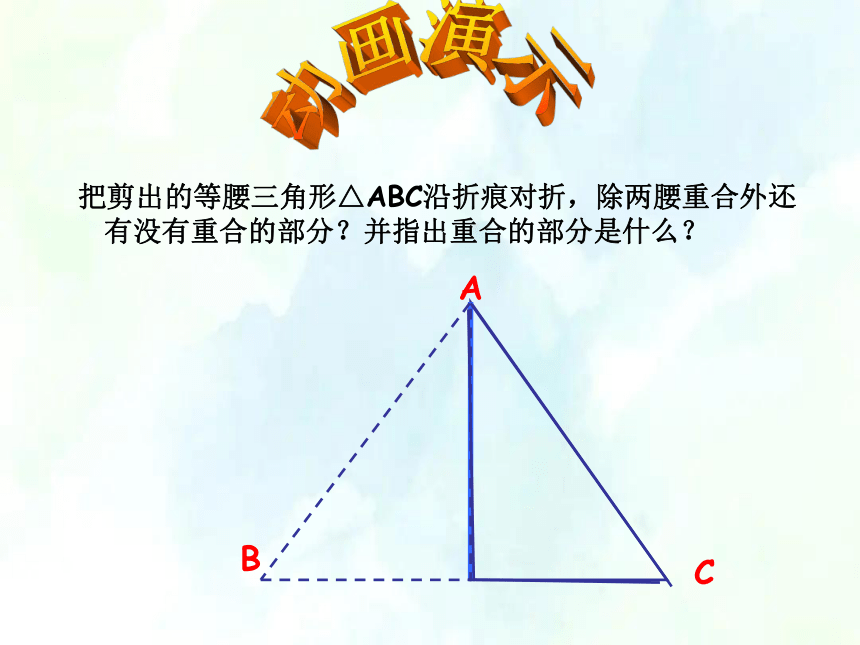
把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
A
B
C
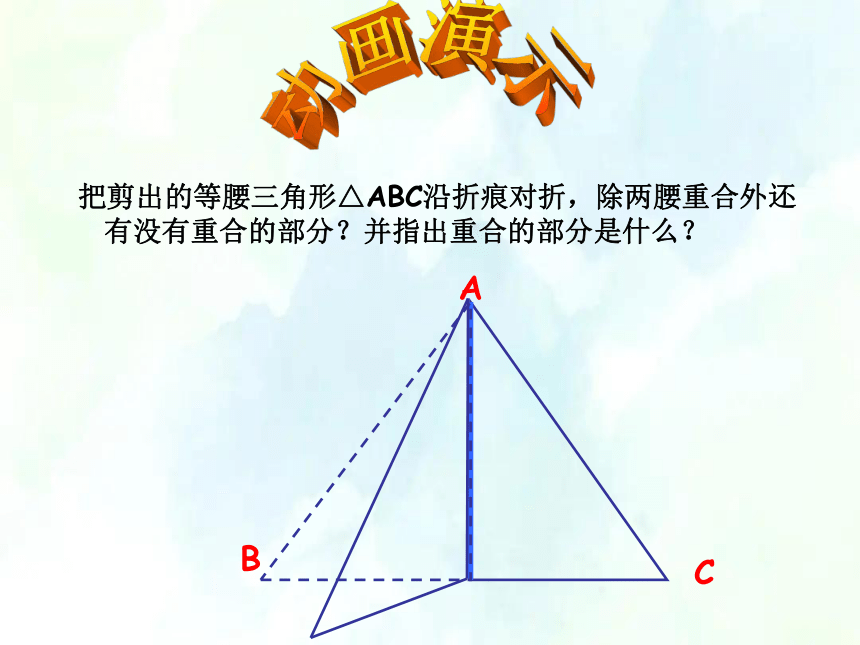
把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
A
B
C
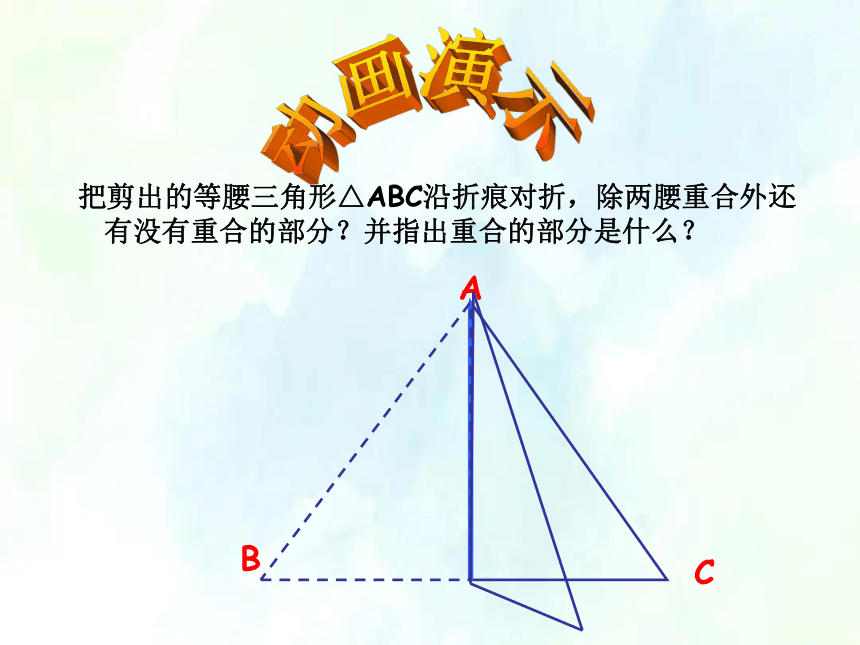
把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
A
B
C
把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
A
B
C
把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
A
B
C
(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
A
B
C
把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
A
B
C
把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
A
B
C
把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
A
C
把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
腰
腰
底角
把剪出的等腰三角形ABC沿折痕AD对折,请你找出其中重合的线段和角,填入下表:
重合的线段 重合的角
所以你们大胆猜想,等腰三角形
BD=CD
AD=AD
∠B =∠C
∠ADB =∠ADC
∠1 =∠2
活动2:细心观察,大胆猜想。
AB=AC
=90°
AD是底边的中线
AD是顶角平分线
AD是底边上的高
具有哪些性质
1、等腰三角形的两个底角相等
辩一辩,证一证
性质1:等腰三角形的两个底角相等.
思考:(1)命题的题设和结论分别是什么?
(2)根据题设与结论,画出图形,并写出已知和求证,最后证明.
几何命题
文字命题
求证:∠B=∠C
已知:如图,在△ABC中,AB=AC
再思考:怎样证明角与角相等呢?通过折叠等腰三角形,你认为本题用什么方法证明∠B=∠C?
添加辅助线,构造两个三角形
证明两个三角形全等
A
B
C
则有∠1=∠2
D
1
2
在△ABD和△ACD中
证明: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
A
B
C
则有 BD=CD
D
在△ABD和△ACD中
证明: 作△ABC 的中线AD
AB=AC
BD=CD
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SSS)
∴ ∠B=∠C
(全等三角形对应角相等)
A
B
C
则有 ∠ADB=∠ADC =90
D
在Rt△ABD和Rt△ACD中
证明: 作△ABC 的高线AD
AB=AC
AD=AD
(公共边)
∴ Rt△ABD≌Rt△ACD
(HL)
∴ ∠B=∠C
(全等三角形对应角相等)
性质1:等腰三角形的两个底角相等
(简写成“等边对等角”)
等腰三角形的性质:
∵ AC=AB
∴∠B=∠C
几何语言:在△ABC中,
练习1(口答):
已知:在△ABC中,AB = AC,
∠A = 50°, 求∠B 和 ∠C的度数。
A
B
C
变式练习:
已知:等腰三角形的一个内角为 50 °, 求另两个角的度数.
探究思考:
A
B
C
如何证明:等腰三角形的性质2:等腰三角形顶角平分线,底边上的高,底边上的中线互相重合?
谢谢!
课题:等腰三角形的性质
1、掌握等腰三角形的性质1;
2、能运用等腰三角形的性质1解决相关问题.
有两条边相等的三角形叫做等腰三角形.
A
C
B
腰
腰
底边
底角
底角
温故知新
顶角
拿出课前剪好的三角形纸片 !
如图,把一张长方形的纸按图中虚线对折,
在对折处剪出一个三
再把三角形展开,观察得到的△ABC有什么特点
A
B
C
AB=AC
活动2:折一折,剪一剪
角形,
△ABC是等腰三角形
A
B
C
把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
A
B
C
把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
A
B
C
把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
A
B
C
把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
A
B
C
把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
A
B
C
(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
A
B
C
把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
A
B
C
把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
A
B
C
把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
A
C
把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
腰
腰
底角
把剪出的等腰三角形ABC沿折痕AD对折,请你找出其中重合的线段和角,填入下表:
重合的线段 重合的角
所以你们大胆猜想,等腰三角形
BD=CD
AD=AD
∠B =∠C
∠ADB =∠ADC
∠1 =∠2
活动2:细心观察,大胆猜想。
AB=AC
=90°
AD是底边的中线
AD是顶角平分线
AD是底边上的高
具有哪些性质
1、等腰三角形的两个底角相等
辩一辩,证一证
性质1:等腰三角形的两个底角相等.
思考:(1)命题的题设和结论分别是什么?
(2)根据题设与结论,画出图形,并写出已知和求证,最后证明.
几何命题
文字命题
求证:∠B=∠C
已知:如图,在△ABC中,AB=AC
再思考:怎样证明角与角相等呢?通过折叠等腰三角形,你认为本题用什么方法证明∠B=∠C?
添加辅助线,构造两个三角形
证明两个三角形全等
A
B
C
则有∠1=∠2
D
1
2
在△ABD和△ACD中
证明: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
A
B
C
则有 BD=CD
D
在△ABD和△ACD中
证明: 作△ABC 的中线AD
AB=AC
BD=CD
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SSS)
∴ ∠B=∠C
(全等三角形对应角相等)
A
B
C
则有 ∠ADB=∠ADC =90
D
在Rt△ABD和Rt△ACD中
证明: 作△ABC 的高线AD
AB=AC
AD=AD
(公共边)
∴ Rt△ABD≌Rt△ACD
(HL)
∴ ∠B=∠C
(全等三角形对应角相等)
性质1:等腰三角形的两个底角相等
(简写成“等边对等角”)
等腰三角形的性质:
∵ AC=AB
∴∠B=∠C
几何语言:在△ABC中,
练习1(口答):
已知:在△ABC中,AB = AC,
∠A = 50°, 求∠B 和 ∠C的度数。
A
B
C
变式练习:
已知:等腰三角形的一个内角为 50 °, 求另两个角的度数.
探究思考:
A
B
C
如何证明:等腰三角形的性质2:等腰三角形顶角平分线,底边上的高,底边上的中线互相重合?
谢谢!
