人教版八年级上册13.3.1 等腰三角形复习动点复习 课件(共13张PPT)
文档属性
| 名称 | 人教版八年级上册13.3.1 等腰三角形复习动点复习 课件(共13张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 464.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-03 19:19:36 | ||
图片预览




文档简介
(共13张PPT)
《等腰三角形》动点问题探究
学习目标
概念:等腰三角形:有两边相等的三角形
性质:
1、等腰三角形两底角相等(等边对等角)
2、等腰三角形顶角的平分线、底边上的高、底边上的中线互相重合(三线合一)
掌握分析动点问题的方法,化动为静;
掌握数形结合思想、方程思想、分类讨论思想等数学思想方法解决动点问题。
中考数学专题复习--等腰三角形动点问题
图形中的点、线、面的运动,构成了数学中的一个新问题----动态问题。在解这类问题时,要充分发挥空间想象的能力,不要被“动”所迷惑,而是要在“动”中求“静”,化“动”为“静”,抓住它运动中的某一瞬间,寻找确定的关系式,就能找到解决问题的途径。
一、试一试,我能行
一个动点:图形中一个动点所形成的等腰三角形问题
例1:如图,已知平行四边形ABCD中AB=7cm,BC=4cm,∠A=30°,点P从点A沿AB边向点B运动,速度为1cm/s。若设运动时间为t(s),连接PC,当t为何值时,ΔPBC为等腰三角形?
提示:如图,连接PC
以BP、BC边为等腰ΔPBC的腰
∴PB=BC 即7-t=4
即:t=3
所以当t=3s时, ΔPBC为等腰三角形
归纳:1、定图形;2、表线段;3、列方程;4、解问题
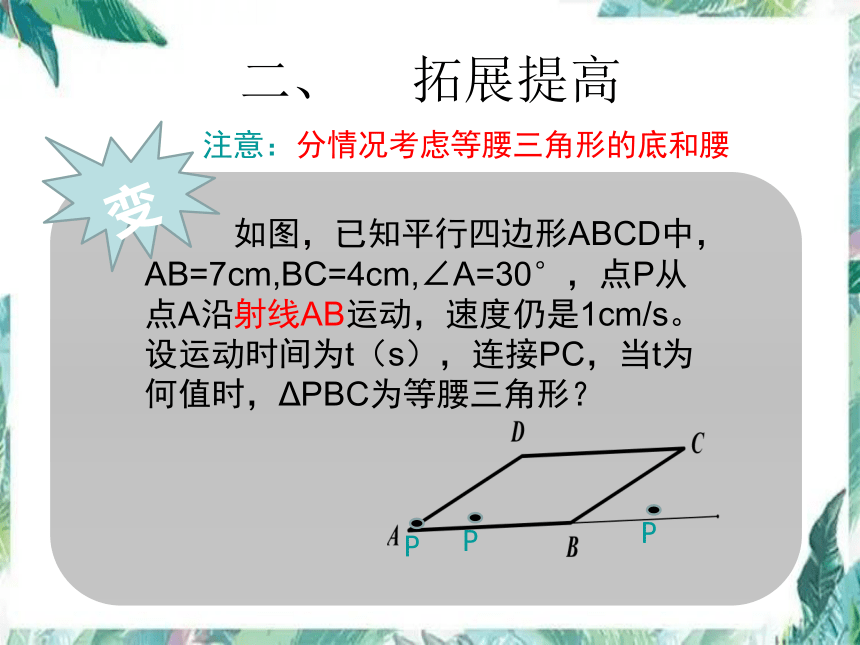
二、 拓展提高
如图,已知平行四边形ABCD中,AB=7cm,BC=4cm,∠A=30°,点P从点A沿射线AB运动,速度仍是1cm/s。设运动时间为t(s),连接PC,当t为何值时,ΔPBC为等腰三角形?
变
P
P
P
注意:分情况考虑等腰三角形的底和腰
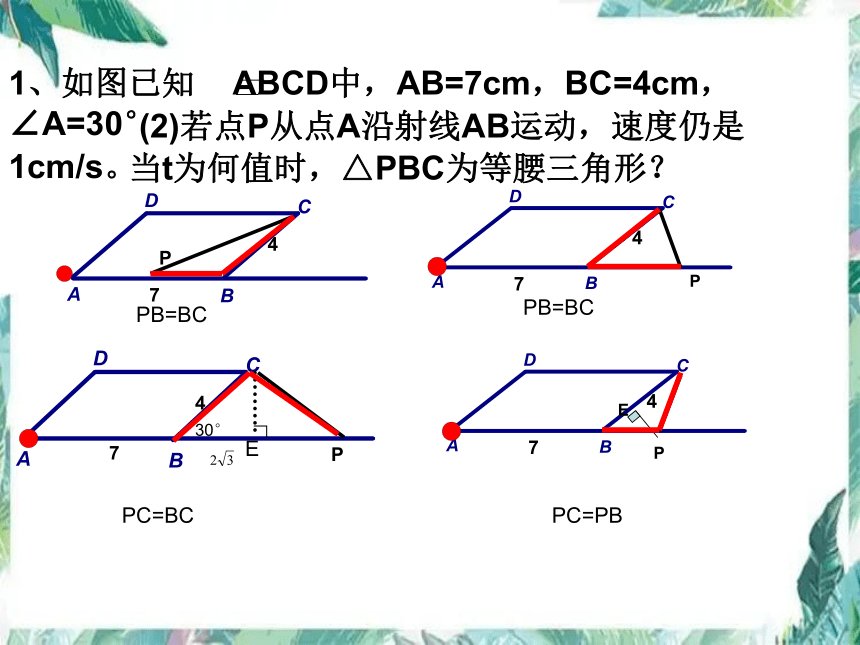
1、如图已知 ABCD中,AB=7cm,BC=4cm,∠A=30°
P
7
4
P
7
4
30°
∟
E
P
7
4
P
E
7
4
(2)若点P从点A沿射线AB运动,速度仍是1cm/s。
当t为何值时,△PBC为等腰三角形?
PB=BC
PB=BC
PC=BC
PC=PB
规范书写,提高得分点
解:如图(1)当以B为顶点时,BP=BC,连接PC,以BP、BC边为腰
∴PB=BC=4,
7-t=4
即:t=3
所以当t=3S时, ΔPBC为等腰三角形
如图(3)以点P为顶点时,PB=PC
连接PC,以BP、PC边为腰,过P作PE⊥BC
∵PB=PC PE⊥BC ∴BE=1/2BC=2
∴ 在RtΔPBE中 cos30 =BE/BP得 PB=
∵ AP=AB+BP ∴ t=
所以,当t= (S)时ΔPBC为等腰三角形
如图(2)以点B为顶点,连接PC,以BP、BC边为腰
∴ PB=BC=4,AP=AB+BP=7+4=11,
即t=11 (S)
所以当t=11S时, ΔPBC为等腰三角形
如图(4)以点C为顶点,CB=CP,连接PC,以BC、PC边为腰,过C作CE⊥BP 在RTΔBEC中 ,cos30 =BE/BC 得 BE==2√3
∵ BC=PC CE⊥BP ∴BP=2BE=4√3
∵ AP=AB+BP
∴ AP= 即:
所以,当t= (S)时ΔPBC为等腰三角形
E
E
综上所述:当t=3s、11s、
时,ΔPBC为等腰三角形
例2.如图,顶点为A的抛物线y=a(x+2)2-4交x轴于点B(1,0),连接AB,过原点O作射线OM∥AB,过点A作AD∥x轴交OM于点D,点C为抛物线与x轴的另一个交点,连接CD.
(1)求抛物线的解析式、直线AB的解析式;
(2)若动点P从点O出发,以每秒1个单位长度的速度沿线段OD向点D运动,同时动点Q从点C出发,以每秒2个单位长度的速度沿线段CO向点O运动,当其中一个点停止运动时另一个点也随之停止运动.
问题1:当t为何值时,△OPQ为等腰三角形?
问题2:当t为何值时,四边形CDPQ的面积最小?并求此时PQ的长.
三:实践新知,提炼应用
1、动点问题的关键:起点,终点,方向,速度,最终用路程表示线段的长。
2 步骤:(1)、定图形;(2)、表线段;(3)、列方程;(4)、解问题
3、常用知识:相似、三角函数、特殊角的性质、面积公式、勾股定理等知识;
六、收获与感悟
收获一:化动为静
收获二:分类讨论
收获三:数形结合
收获四:构建数学模型(如:函数模型,方程模型,直角三角形模型,相似模型等)
数学思想:
1,如图,已知四边形ABCD中,AD∥BC ,∠B=90°,AD=24cm,BC=26cm,动点P从点A开始沿AD边向点D,以1cm/秒的速度运动,动点Q从点C开始沿CB向点B以3厘米/秒的速度运动,P、Q分别从点A点C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒,求:
1)t为何值时,四边形PQCD为平行四边形
2) t为何值时,PQ=CD?
作业:
1t
3t
2、如图,矩形ABCD中,AB=6,BC= ,
点O是AB的中点,点P在AB的延长线上,
且BP=3。一动点E从O点出发,以每秒1
个单位长度的速度沿OA匀速运动,到
达A点后,立即以原速度沿AO返回;另
一动点F从P点发发,以每秒1个单位长
度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧。设运动的时间为t秒(t≥0)。
(1)当等边△EFG的边FG恰好经过点C时,求运动时间t的值;
(2)在整个运动过程中,设等边△EFG和矩形ABCD重叠部分的面积为S,请直接写出S与t之间的函数关系式和相应的自变量t的取值范围;
(3)设EG与矩形ABCD的对角线AC的交点为H,是否存在这样的t ,使△AOH是等腰三角形?若存大,求出对应的t的值;若不存在,请说明理由。
谢谢!
请各位老师批评指正!
预祝各位同学中考考出理想的成绩!
《等腰三角形》动点问题探究
学习目标
概念:等腰三角形:有两边相等的三角形
性质:
1、等腰三角形两底角相等(等边对等角)
2、等腰三角形顶角的平分线、底边上的高、底边上的中线互相重合(三线合一)
掌握分析动点问题的方法,化动为静;
掌握数形结合思想、方程思想、分类讨论思想等数学思想方法解决动点问题。
中考数学专题复习--等腰三角形动点问题
图形中的点、线、面的运动,构成了数学中的一个新问题----动态问题。在解这类问题时,要充分发挥空间想象的能力,不要被“动”所迷惑,而是要在“动”中求“静”,化“动”为“静”,抓住它运动中的某一瞬间,寻找确定的关系式,就能找到解决问题的途径。
一、试一试,我能行
一个动点:图形中一个动点所形成的等腰三角形问题
例1:如图,已知平行四边形ABCD中AB=7cm,BC=4cm,∠A=30°,点P从点A沿AB边向点B运动,速度为1cm/s。若设运动时间为t(s),连接PC,当t为何值时,ΔPBC为等腰三角形?
提示:如图,连接PC
以BP、BC边为等腰ΔPBC的腰
∴PB=BC 即7-t=4
即:t=3
所以当t=3s时, ΔPBC为等腰三角形
归纳:1、定图形;2、表线段;3、列方程;4、解问题
二、 拓展提高
如图,已知平行四边形ABCD中,AB=7cm,BC=4cm,∠A=30°,点P从点A沿射线AB运动,速度仍是1cm/s。设运动时间为t(s),连接PC,当t为何值时,ΔPBC为等腰三角形?
变
P
P
P
注意:分情况考虑等腰三角形的底和腰
1、如图已知 ABCD中,AB=7cm,BC=4cm,∠A=30°
P
7
4
P
7
4
30°
∟
E
P
7
4
P
E
7
4
(2)若点P从点A沿射线AB运动,速度仍是1cm/s。
当t为何值时,△PBC为等腰三角形?
PB=BC
PB=BC
PC=BC
PC=PB
规范书写,提高得分点
解:如图(1)当以B为顶点时,BP=BC,连接PC,以BP、BC边为腰
∴PB=BC=4,
7-t=4
即:t=3
所以当t=3S时, ΔPBC为等腰三角形
如图(3)以点P为顶点时,PB=PC
连接PC,以BP、PC边为腰,过P作PE⊥BC
∵PB=PC PE⊥BC ∴BE=1/2BC=2
∴ 在RtΔPBE中 cos30 =BE/BP得 PB=
∵ AP=AB+BP ∴ t=
所以,当t= (S)时ΔPBC为等腰三角形
如图(2)以点B为顶点,连接PC,以BP、BC边为腰
∴ PB=BC=4,AP=AB+BP=7+4=11,
即t=11 (S)
所以当t=11S时, ΔPBC为等腰三角形
如图(4)以点C为顶点,CB=CP,连接PC,以BC、PC边为腰,过C作CE⊥BP 在RTΔBEC中 ,cos30 =BE/BC 得 BE==2√3
∵ BC=PC CE⊥BP ∴BP=2BE=4√3
∵ AP=AB+BP
∴ AP= 即:
所以,当t= (S)时ΔPBC为等腰三角形
E
E
综上所述:当t=3s、11s、
时,ΔPBC为等腰三角形
例2.如图,顶点为A的抛物线y=a(x+2)2-4交x轴于点B(1,0),连接AB,过原点O作射线OM∥AB,过点A作AD∥x轴交OM于点D,点C为抛物线与x轴的另一个交点,连接CD.
(1)求抛物线的解析式、直线AB的解析式;
(2)若动点P从点O出发,以每秒1个单位长度的速度沿线段OD向点D运动,同时动点Q从点C出发,以每秒2个单位长度的速度沿线段CO向点O运动,当其中一个点停止运动时另一个点也随之停止运动.
问题1:当t为何值时,△OPQ为等腰三角形?
问题2:当t为何值时,四边形CDPQ的面积最小?并求此时PQ的长.
三:实践新知,提炼应用
1、动点问题的关键:起点,终点,方向,速度,最终用路程表示线段的长。
2 步骤:(1)、定图形;(2)、表线段;(3)、列方程;(4)、解问题
3、常用知识:相似、三角函数、特殊角的性质、面积公式、勾股定理等知识;
六、收获与感悟
收获一:化动为静
收获二:分类讨论
收获三:数形结合
收获四:构建数学模型(如:函数模型,方程模型,直角三角形模型,相似模型等)
数学思想:
1,如图,已知四边形ABCD中,AD∥BC ,∠B=90°,AD=24cm,BC=26cm,动点P从点A开始沿AD边向点D,以1cm/秒的速度运动,动点Q从点C开始沿CB向点B以3厘米/秒的速度运动,P、Q分别从点A点C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒,求:
1)t为何值时,四边形PQCD为平行四边形
2) t为何值时,PQ=CD?
作业:
1t
3t
2、如图,矩形ABCD中,AB=6,BC= ,
点O是AB的中点,点P在AB的延长线上,
且BP=3。一动点E从O点出发,以每秒1
个单位长度的速度沿OA匀速运动,到
达A点后,立即以原速度沿AO返回;另
一动点F从P点发发,以每秒1个单位长
度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧。设运动的时间为t秒(t≥0)。
(1)当等边△EFG的边FG恰好经过点C时,求运动时间t的值;
(2)在整个运动过程中,设等边△EFG和矩形ABCD重叠部分的面积为S,请直接写出S与t之间的函数关系式和相应的自变量t的取值范围;
(3)设EG与矩形ABCD的对角线AC的交点为H,是否存在这样的t ,使△AOH是等腰三角形?若存大,求出对应的t的值;若不存在,请说明理由。
谢谢!
请各位老师批评指正!
预祝各位同学中考考出理想的成绩!
