怎样判定三角形全等

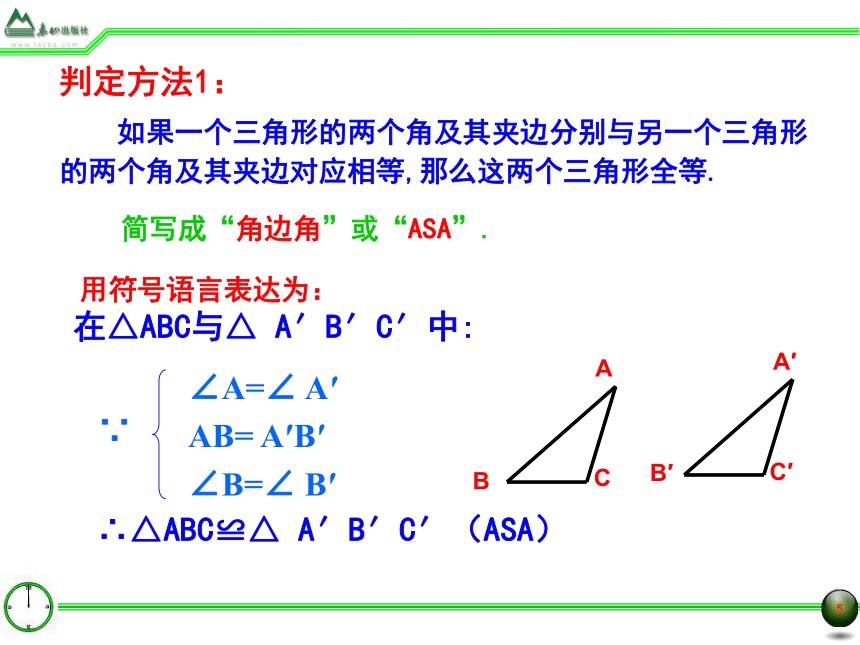
课件12张PPT。§8.3怎样判定三角形全等（第一课时）第8章 平面图形的全等与相似 如果已知一个三角形的两角及一边，那么有几种可能的情况呢？答：角边角（ASA） 角角边（AAS）实验与探究问题1：问题2：做一做：已知：∠ = 700、∠ = 500、a = 5厘米。在硬纸片上画出⊿ABC，使∠B = ∠ 、∠C = ∠ 、BC = a。 剪下你画出的三角形，与其他同学剪得的三角形进行比较，这些三角形能重合吗？问题3：问题4：做一做：改变∠ ,∠ 的大小(∠ +∠ ＜ 1800 )或改变线段a的长短,按同一条件与同学再做一次,所剪得的三角形还能重合吗? 通过上面的实验,你能得到什么结论?与同学交流.用符号语言表达为：在△ABC与△ A′B′C′中:∴△ABC≌△ A′B′C′（ASA） 如果一个三角形的两个角及其夹边分别与另一个三角形的两个角及其夹边对应相等,那么这两个三角形全等. 简写成“角边角”或“ASA”.判定方法1：∵∠A=∠ A′
AB= A′B′
∠B=∠ B′∠1=∠2（已知）
BD=DB (公共边）
∠3=∠4 （已知）解：全等。
在 ABD和 CDB中，
∵∴≌(ASA)∴△ABC≌△DEF (ASA）∠B=∠E (已知）
BC=EF （已知）
∠C=∠F （已证）
解（1）相等。
∵∠C=180°-∠A-∠B , ∠F=180°-∠D-∠E又 ∠A=∠D , ∠B=∠E
∴∠C=∠F
（2）全等。在△ABC和△DEF中，
∵
结论 如果一个三角形的两个角及其中一角的对边分别与另一个三角形的两个角及其中一角的对边对应相等,那么这两个三角形全等.
这个判定方法可以简单地用“角角边” 或“ AAS”来表示.用符号语言表达为：在△ABC与△ A′B′C′中:∴△ABC≌△ A′B′C′（AAS）∵∠A=∠ A′
∠B=∠ B′
BC= B′C′小结(1) 两角和它们的夹边对应相等的两个三角形全等. 简写成“角边角”或“ASA”.(2) 两角和其中一角的对边对应相等的两个三角形全等.简写成“角角边”或“AAS”.知识要点：（3）探索三角形全等是证明线段相等（对应边相等），角
相等（对应角相等）等问题的基本途径。数学思想：要学会用分类的思想，转化的思想解决问题。再 见