6.4.组合图形的面积(课件)-五年级上册数学人教版 (共17张PPT)
文档属性
| 名称 | 6.4.组合图形的面积(课件)-五年级上册数学人教版 (共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 520.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-03 19:16:18 | ||
图片预览



文档简介
(共17张PPT)
6.4 组合图形的面积
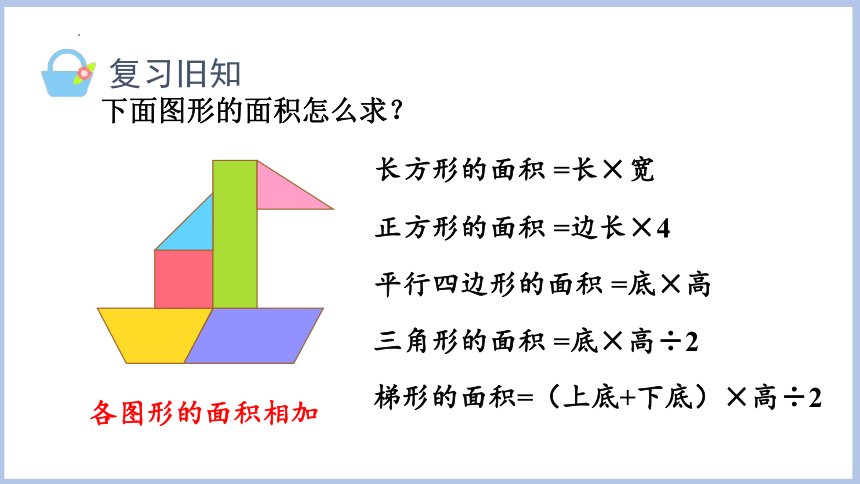
下面图形的面积怎么求?
各图形的面积相加
长方形的面积 =长×宽
正方形的面积 =边长×4
平行四边形的面积 =底×高
三角形的面积 =底×高÷2
梯形的面积=(上底+下底)×高÷2
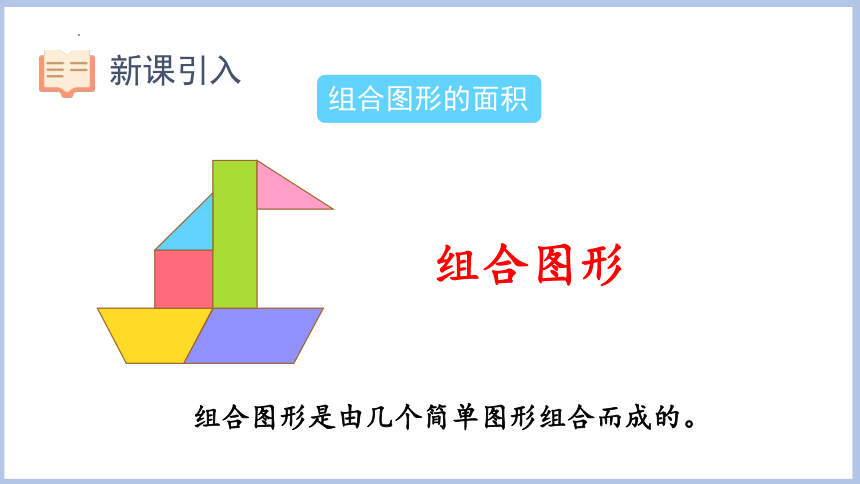
组合图形
组合图形是由几个简单图形组合而成的。
组合图形的面积
欣赏
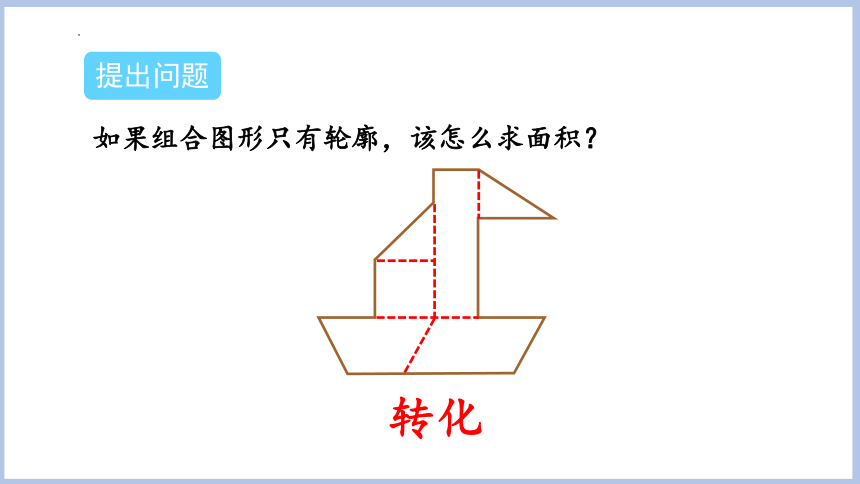
提出问题
如果组合图形只有轮廓,该怎么求面积?
转化
主动探究
右图表示的是一间房子侧面墙的形状。它的面积是多少平方米?
5m
1.想一想:这个组合图形可以转化为哪些基本图形?
2.画一画:用虚线把你们的想法表示在图上。
3.说一说:你想怎样计算图形的面积。
4.算一算:找出求面积所需的条件,并算出图形的面积。
2m
5m
5m
2m
5m
5m
+
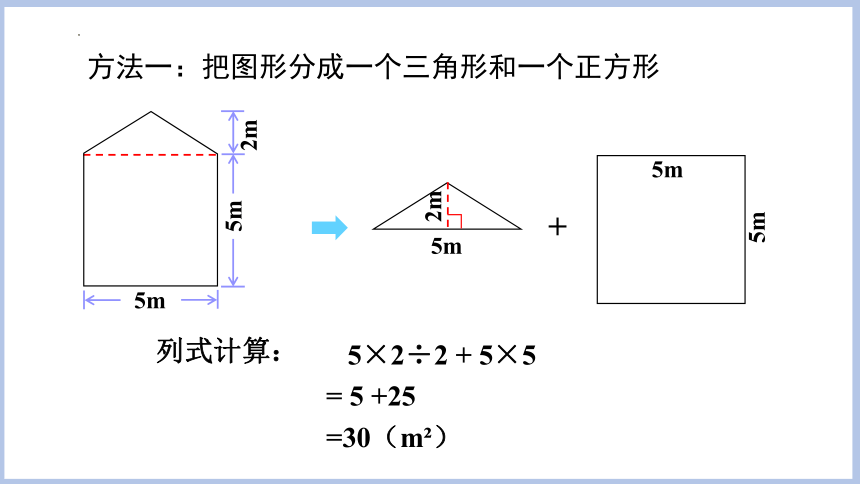
5×2÷2 + 5×5
= 5 +25
=30(m )
列式计算:
5m
2m
5m
方法一:把图形分成一个三角形和一个正方形
2m
+
(5 + 2 + 5)×(5÷2)÷2×2
= 12×2.5÷2×2
=30(m )
列式计算:
5m
2m
(5÷2)m
2m
(5÷2)m
5m
5m
5m
方法二:把图形分成两个完全相同的梯形
方法三:添上两个三角形,使图形变成长方形
-
2m
5m
5m
2m
(5 + 2)× 5 -(5÷2)×2÷2×2
= 35 - 5
=30(m )
列式计算:
5m
5m
2m
5m
方法四:把图形割补成一个长方形
(5 + 2÷2)× 5
= 6×5
=30(m )
列式计算:
5m
5m
5m
(2÷2)m
5m
2m
讨论优化
你更喜欢哪种方法?为什么?
简便
数学思想
你能给这几种方法分分类吗?
分割法
添补法
割补法
下图中这面旗子的面积是多少?
1.
方法一:
分成一个正方形和两个三角形
(80-20)×(30+30)+30×20÷2×2
= 60×60 + 600÷2×2
= 3600 + 600
= 4200(cm )
答:这面旗子的面积是4200cm 。
下图中这面旗子的面积是多少?
1.
方法二:分成两个一样的梯形
(80-20 + 80)×30÷2×2
= 140×30÷2×2
= 4200 ÷2×2
= 4200(cm )
答:这面旗子的面积是4200cm 。
下图中这面旗子的面积是多少?
1.
方法三:变成一个长方形
80×(30 + 30)-(30+30)×20÷2
= 80×60 - 60×20÷2
= 4800 – 1200÷2
= 4200(cm )
答:这面旗子的面积是4200cm 。
在一块梯形的地中间有一个长方形的游泳池,其余的地方是草地。草地的面积是多少平方米?
2.
(70+40)×30÷2-30×15
=110×30÷2-450
=1650-450
=1200(m2)
答:草地的面积是1200平方米。
组合面积小窍门
组合图形面积藏,转化思想来帮忙;
分割方法仔细辨,基本图形面积加;
添补方法变整体,基本图形面积减;
割补方法变图形,前后面积不改变;
组合面积方法多,随机应变你最强!
6.4 组合图形的面积
下面图形的面积怎么求?
各图形的面积相加
长方形的面积 =长×宽
正方形的面积 =边长×4
平行四边形的面积 =底×高
三角形的面积 =底×高÷2
梯形的面积=(上底+下底)×高÷2
组合图形
组合图形是由几个简单图形组合而成的。
组合图形的面积
欣赏
提出问题
如果组合图形只有轮廓,该怎么求面积?
转化
主动探究
右图表示的是一间房子侧面墙的形状。它的面积是多少平方米?
5m
1.想一想:这个组合图形可以转化为哪些基本图形?
2.画一画:用虚线把你们的想法表示在图上。
3.说一说:你想怎样计算图形的面积。
4.算一算:找出求面积所需的条件,并算出图形的面积。
2m
5m
5m
2m
5m
5m
+
5×2÷2 + 5×5
= 5 +25
=30(m )
列式计算:
5m
2m
5m
方法一:把图形分成一个三角形和一个正方形
2m
+
(5 + 2 + 5)×(5÷2)÷2×2
= 12×2.5÷2×2
=30(m )
列式计算:
5m
2m
(5÷2)m
2m
(5÷2)m
5m
5m
5m
方法二:把图形分成两个完全相同的梯形
方法三:添上两个三角形,使图形变成长方形
-
2m
5m
5m
2m
(5 + 2)× 5 -(5÷2)×2÷2×2
= 35 - 5
=30(m )
列式计算:
5m
5m
2m
5m
方法四:把图形割补成一个长方形
(5 + 2÷2)× 5
= 6×5
=30(m )
列式计算:
5m
5m
5m
(2÷2)m
5m
2m
讨论优化
你更喜欢哪种方法?为什么?
简便
数学思想
你能给这几种方法分分类吗?
分割法
添补法
割补法
下图中这面旗子的面积是多少?
1.
方法一:
分成一个正方形和两个三角形
(80-20)×(30+30)+30×20÷2×2
= 60×60 + 600÷2×2
= 3600 + 600
= 4200(cm )
答:这面旗子的面积是4200cm 。
下图中这面旗子的面积是多少?
1.
方法二:分成两个一样的梯形
(80-20 + 80)×30÷2×2
= 140×30÷2×2
= 4200 ÷2×2
= 4200(cm )
答:这面旗子的面积是4200cm 。
下图中这面旗子的面积是多少?
1.
方法三:变成一个长方形
80×(30 + 30)-(30+30)×20÷2
= 80×60 - 60×20÷2
= 4800 – 1200÷2
= 4200(cm )
答:这面旗子的面积是4200cm 。
在一块梯形的地中间有一个长方形的游泳池,其余的地方是草地。草地的面积是多少平方米?
2.
(70+40)×30÷2-30×15
=110×30÷2-450
=1650-450
=1200(m2)
答:草地的面积是1200平方米。
组合面积小窍门
组合图形面积藏,转化思想来帮忙;
分割方法仔细辨,基本图形面积加;
添补方法变整体,基本图形面积减;
割补方法变图形,前后面积不改变;
组合面积方法多,随机应变你最强!
