人教版五年级上册数学6.5.不规则图形的面积课件(共11张PPT)
文档属性
| 名称 | 人教版五年级上册数学6.5.不规则图形的面积课件(共11张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-03 00:00:00 | ||
图片预览




文档简介
(共11张PPT)
6.5 不规则图形的面积
那像树叶、手掌,这样的不规则图形该如何计算它们的面积呢?
我们已经学过了很多种规则图形面积的计算方法。
新课引入
图中每个小方格的面积是1cm2,请你估计这片叶子的面积。
探究活动
1.这片叶子的形状不规则,怎样计算面积呢?
2.可以在图上标一标、画一画,想好后再小组间进行
交流,看谁的方法最多。
先在叶子上画出所有的方格线,
满格的一共有18格,面积一定大于18cm2,
不是满格的也有18格,面积一定小于36cm2,
因此,这片叶子的面积在18cm2至36cm2之间。
如果把不满一格的都按半格计算,这片叶子的面积大约是27cm2。
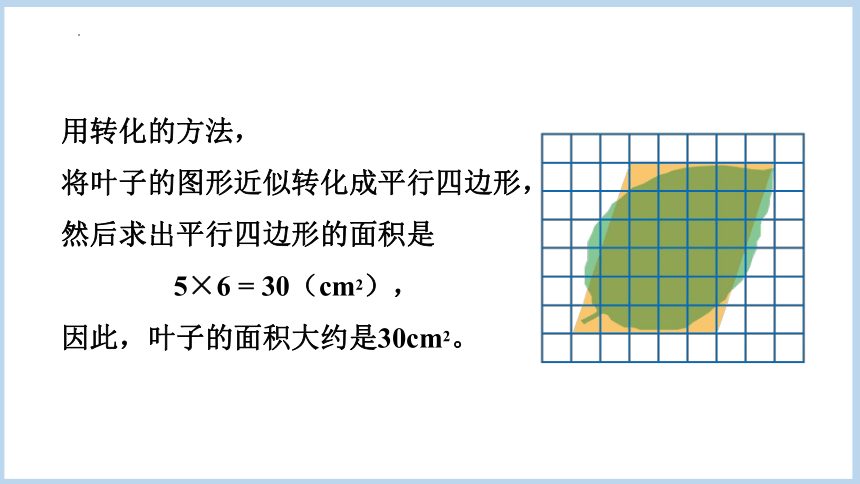
用转化的方法,
将叶子的图形近似转化成平行四边形,
然后求出平行四边形的面积是
5×6 = 30(cm2),
因此,叶子的面积大约是30cm2。
用转化的方法,
将叶子的图形近似转化成长方形,
然后求出长方形的面积是
5×6 = 30(cm2),
因此,叶子的面积大约是30cm2。
怎样估计不规则图形的面积?
可以通过数方格确定图形面积的范围,然后再估算图形的面积;
也可以把不规则的图形转化为学过的图形进行估算。
1.有一块地近似平行四边形,形状如右图,这块地的面
积约是多少平方米 (得数保留整数。)
43×20.1≈864(m2)
答:这块地的面积约是864m2。
43m
20.1m
巩固练转化成长方形
8×4 = 32(cm2)
涂色部分面积大约是 32cm2。
2.图中每个小方格的面积为1cm2,计算涂色部分的
面积。
巩固练习
3.图中每个小方格的面积为1m2,请你估计这个池塘的面积。
近似转化成长方形,
然后求出长方形的面积是12×8 = 96(cm2),
因此,池塘的面积大约是96cm2。
12
8
阅读与理解
回顾与反思
分析与解答
6.5 不规则图形的面积
那像树叶、手掌,这样的不规则图形该如何计算它们的面积呢?
我们已经学过了很多种规则图形面积的计算方法。
新课引入
图中每个小方格的面积是1cm2,请你估计这片叶子的面积。
探究活动
1.这片叶子的形状不规则,怎样计算面积呢?
2.可以在图上标一标、画一画,想好后再小组间进行
交流,看谁的方法最多。
先在叶子上画出所有的方格线,
满格的一共有18格,面积一定大于18cm2,
不是满格的也有18格,面积一定小于36cm2,
因此,这片叶子的面积在18cm2至36cm2之间。
如果把不满一格的都按半格计算,这片叶子的面积大约是27cm2。
用转化的方法,
将叶子的图形近似转化成平行四边形,
然后求出平行四边形的面积是
5×6 = 30(cm2),
因此,叶子的面积大约是30cm2。
用转化的方法,
将叶子的图形近似转化成长方形,
然后求出长方形的面积是
5×6 = 30(cm2),
因此,叶子的面积大约是30cm2。
怎样估计不规则图形的面积?
可以通过数方格确定图形面积的范围,然后再估算图形的面积;
也可以把不规则的图形转化为学过的图形进行估算。
1.有一块地近似平行四边形,形状如右图,这块地的面
积约是多少平方米 (得数保留整数。)
43×20.1≈864(m2)
答:这块地的面积约是864m2。
43m
20.1m
巩固练转化成长方形
8×4 = 32(cm2)
涂色部分面积大约是 32cm2。
2.图中每个小方格的面积为1cm2,计算涂色部分的
面积。
巩固练习
3.图中每个小方格的面积为1m2,请你估计这个池塘的面积。
近似转化成长方形,
然后求出长方形的面积是12×8 = 96(cm2),
因此,池塘的面积大约是96cm2。
12
8
阅读与理解
回顾与反思
分析与解答
