人教版 八年级上册 13.3.1等腰三角形 优质课件 (共17张PPT)
文档属性
| 名称 | 人教版 八年级上册 13.3.1等腰三角形 优质课件 (共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 999.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-03 19:48:03 | ||
图片预览




文档简介
(共17张PPT)
1、动手操作,探究新知
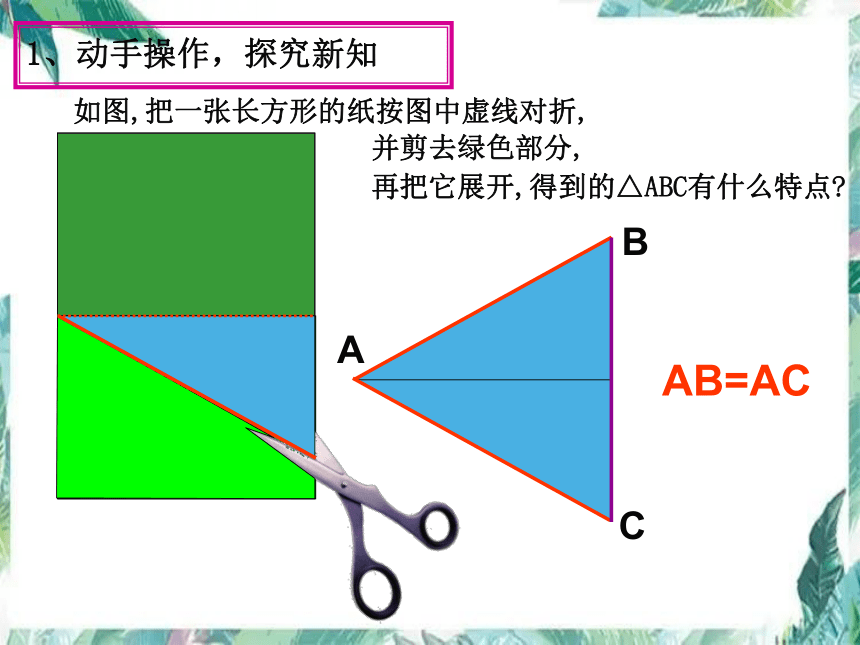
如图,把一张长方形的纸按图中虚线对折,
并剪去绿色部分,
再把它展开,得到的△ABC有什么特点
A
B
C
AB=AC
1、动手操作,探究新知
A
B
C
有两条边相等的三角形,叫做等腰三角形
相等的两条边叫做腰
另一条边叫做底边
底边与腰的夹角叫做底角
两腰所夹的角叫做顶角
腰
腰
底边
顶角
底角
等腰三角形
1、动手操作,探究新知
A
C
B
D
D
A
B
C
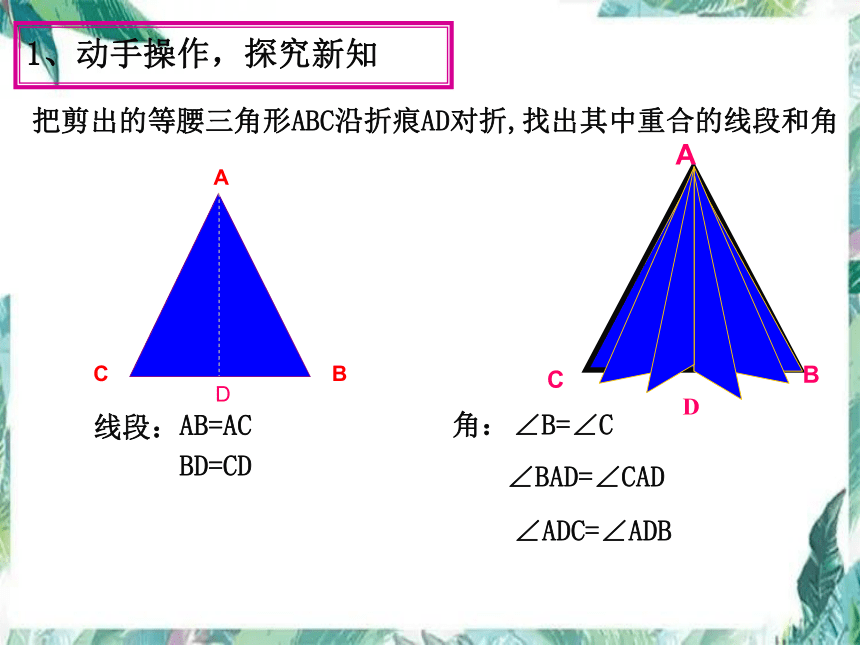
把剪出的等腰三角形ABC沿折痕AD对折,找出其中重合的线段和角
线段:
AB=AC
BD=CD
角:
∠B=∠C
∠BAD=∠CAD
∠ADC=∠ADB
2、证明猜想,获得新知
猜想1:等腰三角形的两个底角相等
已知:在△ABC中,AB=AC
求证:∠B=∠C
A
B
C
问题
引领
1、想一想我们学过哪些证明角和角相等的方法?
2、通过折叠等腰三角形纸片,你认为本题应用
哪种方法证明∠B=∠C。
3、你认为通过什么方法可以构造两
个全等的三角形?
2、证明猜想,获得新知
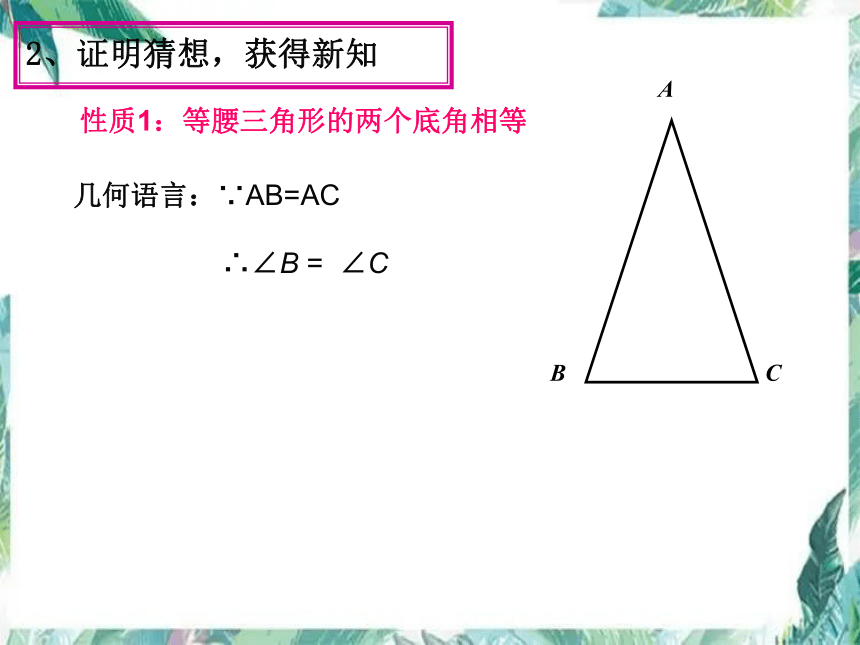
性质1:等腰三角形的两个底角相等
几何语言:∵AB=AC
A
B
C
∴∠B = ∠C
性质2:等腰三角形的顶角平分线、底边上的中线、
底边上的高互相重合
2、证明猜想,获得新知
BD=CD
∠BAD=∠CAD
AD⊥BC
∠BAD=∠CAD
BD=CD
AD⊥BC
AD⊥BC
BD=CD
∠BAD=∠CAD
△ABC中,AB=AC,----------------------
------------- ----------------
(三)
∴
∵
△ABC中,AB=AC,----------------------
------------- ----------------
∴
∵
(一)
A
B
D
C
△ABC中,AB=AC,----------------------
------------- ----------------
∴
∵
(二)
2、证明猜想,获得新知
这两个性质是等腰三角形特有的性质吗?
3、例题讲解,应用新知
例1、 在下列的等腰三角形中,分别求出它们的底角的度数 .
⌒
40°
⌒
120°
∟
70°
︵
70°
︵
30°
︵
45°
︵
︵
30°
︵
45°
3、例题讲解,应用新知
例2:在等腰△ABC中,AB =AC, ∠A = 50°,
①等腰三角形中已知一个角可以求出另两个角
② 0°<顶角<180°, 0°<底角<90°
则另外两个角的度数为 .
变式1:在等腰△ABC中,∠A =50°,
则另外两个角的度数为 .
65°, 65°
65°, 65°或50°, 80°
变式2:在等腰△ABC中,∠A =100°,
则另外两个角的度数为 .
40°, 40°
3、例题讲解,应用新知
如图,厂房屋顶钢架外框是等腰三角形,
其中AB=AC,,立柱AD⊥BC.已知∠B=30°,
BC=6m,那么∠BAC=-----------,BD=-----------
120°
3m
例3:
1、动手操作,探究新知
如图,把一张长方形的纸按图中虚线对折,
并剪去绿色部分,
再把它展开,得到的△ABC有什么特点
A
B
C
AB=AC
1、动手操作,探究新知
A
B
C
有两条边相等的三角形,叫做等腰三角形
相等的两条边叫做腰
另一条边叫做底边
底边与腰的夹角叫做底角
两腰所夹的角叫做顶角
腰
腰
底边
顶角
底角
等腰三角形
1、动手操作,探究新知
A
C
B
D
D
A
B
C
把剪出的等腰三角形ABC沿折痕AD对折,找出其中重合的线段和角
线段:
AB=AC
BD=CD
角:
∠B=∠C
∠BAD=∠CAD
∠ADC=∠ADB
2、证明猜想,获得新知
猜想1:等腰三角形的两个底角相等
已知:在△ABC中,AB=AC
求证:∠B=∠C
A
B
C
问题
引领
1、想一想我们学过哪些证明角和角相等的方法?
2、通过折叠等腰三角形纸片,你认为本题应用
哪种方法证明∠B=∠C。
3、你认为通过什么方法可以构造两
个全等的三角形?
2、证明猜想,获得新知
性质1:等腰三角形的两个底角相等
几何语言:∵AB=AC
A
B
C
∴∠B = ∠C
性质2:等腰三角形的顶角平分线、底边上的中线、
底边上的高互相重合
2、证明猜想,获得新知
BD=CD
∠BAD=∠CAD
AD⊥BC
∠BAD=∠CAD
BD=CD
AD⊥BC
AD⊥BC
BD=CD
∠BAD=∠CAD
△ABC中,AB=AC,----------------------
------------- ----------------
(三)
∴
∵
△ABC中,AB=AC,----------------------
------------- ----------------
∴
∵
(一)
A
B
D
C
△ABC中,AB=AC,----------------------
------------- ----------------
∴
∵
(二)
2、证明猜想,获得新知
这两个性质是等腰三角形特有的性质吗?
3、例题讲解,应用新知
例1、 在下列的等腰三角形中,分别求出它们的底角的度数 .
⌒
40°
⌒
120°
∟
70°
︵
70°
︵
30°
︵
45°
︵
︵
30°
︵
45°
3、例题讲解,应用新知
例2:在等腰△ABC中,AB =AC, ∠A = 50°,
①等腰三角形中已知一个角可以求出另两个角
② 0°<顶角<180°, 0°<底角<90°
则另外两个角的度数为 .
变式1:在等腰△ABC中,∠A =50°,
则另外两个角的度数为 .
65°, 65°
65°, 65°或50°, 80°
变式2:在等腰△ABC中,∠A =100°,
则另外两个角的度数为 .
40°, 40°
3、例题讲解,应用新知
如图,厂房屋顶钢架外框是等腰三角形,
其中AB=AC,,立柱AD⊥BC.已知∠B=30°,
BC=6m,那么∠BAC=-----------,BD=-----------
120°
3m
例3:
