人教版 八年级上册13.3.1 等腰三角形的判定 精品课件(共47张PPT)
文档属性
| 名称 | 人教版 八年级上册13.3.1 等腰三角形的判定 精品课件(共47张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-03 00:00:00 | ||
图片预览








文档简介
(共47张PPT)
19.4.2 等腰三角形的判定
思考:“等腰三角形的两个底角相等”的逆命题是什么?
逆命题:
如果一个三角形有两个角相等,那么这两
个角所对的边也相等
探究新知
● 操作一
做一做
你发现了什么结论?其他同学的结果与你的相同吗?
● 操作二
量一量,线段AB与AC的长度。
画△ABC.使∠B=∠C=30°
活动一:
A
B
C
D
1
2
已知:如图,在ΔABC中,∠B=∠C。
求证:AB=AC
证明:
作∠BAC的平分线AD
∵ AD平分∠BAC
∴ ∠1=∠2
在△BAD和△CAD中
如果一个三角形有两个角相等,那么这两
个角所对的边也相等
∠B=∠C
∠1=∠2
AD=AD (公共边)
∴ AB= AC (全等三角形的对应边相等)
∴ △BAD ≌ △CAD (AAS)
活动三:
A
B
C
D
已知:如图,在ΔABC中,∠B=∠C。
求证:AB=AC
证明:
作AD⊥BC
∵ AD ⊥BC
∴∠ADB=∠ADC=90°
在△BAD和△CAD中
如果一个三角形有两个角相等,那么这两
个角所对的边也相等
∠B=∠C
AD=AD (公共边)
∴ AB= AC (全等三角形的对应边相等)
∴ △BAD ≌ △CAD (AAS)
∠ADB=∠ADC
活动三:
A
B
C
D
已知:如图,在ΔABC中,∠B=∠C。
求证:AB=AC
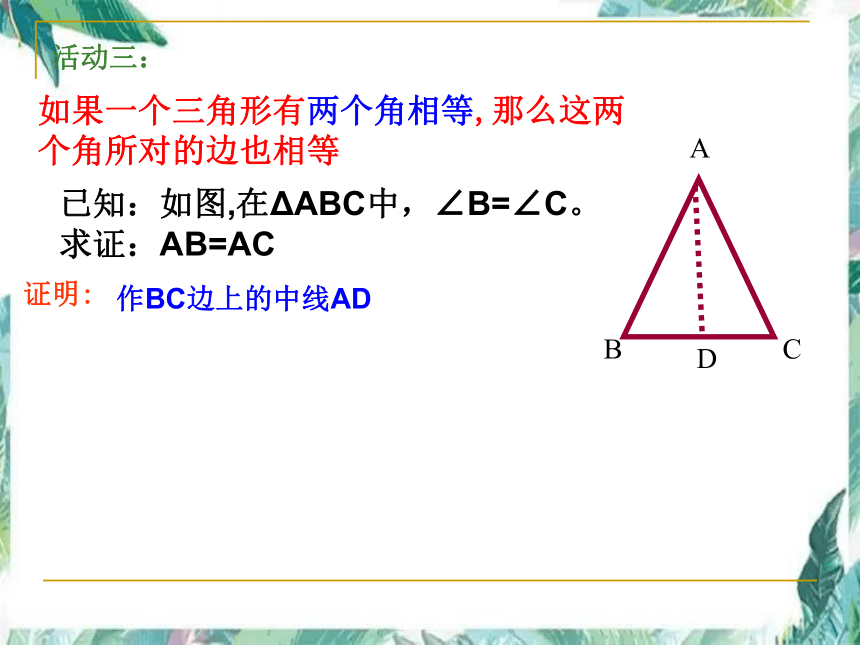
如果一个三角形有两个角相等,那么这两
个角所对的边也相等
活动三:
证明:
作BC边上的中线AD
A
B
C
如果一个三角形有两个角相等,那么这两个角所对的边也相等
几何语言:
∵∠B =∠C (已知)
∴ AB=AC(等角对等边)
等腰三角形的判定定理:
(简写成“等角对等边”)。
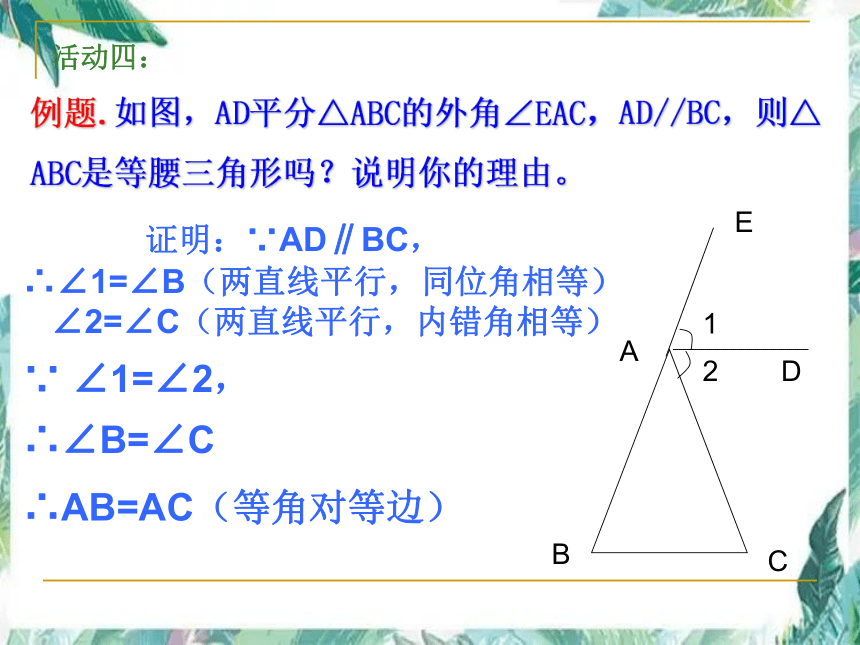
例题.如图,AD平分△ABC的外角∠EAC,AD//BC,则△ ABC是等腰三角形吗?说明你的理由。
证明:∵AD∥BC,
A
E
B
C
1
2
D
∴∠1=∠B(两直线平行,同位角相等)
∠2=∠C(两直线平行,内错角相等)
∵ ∠1=∠2,
∴∠B=∠C
∴AB=AC(等角对等边)
活动四:
巩固新知:1. 下列两个图形是否是等腰三角形?
750
300
400
400
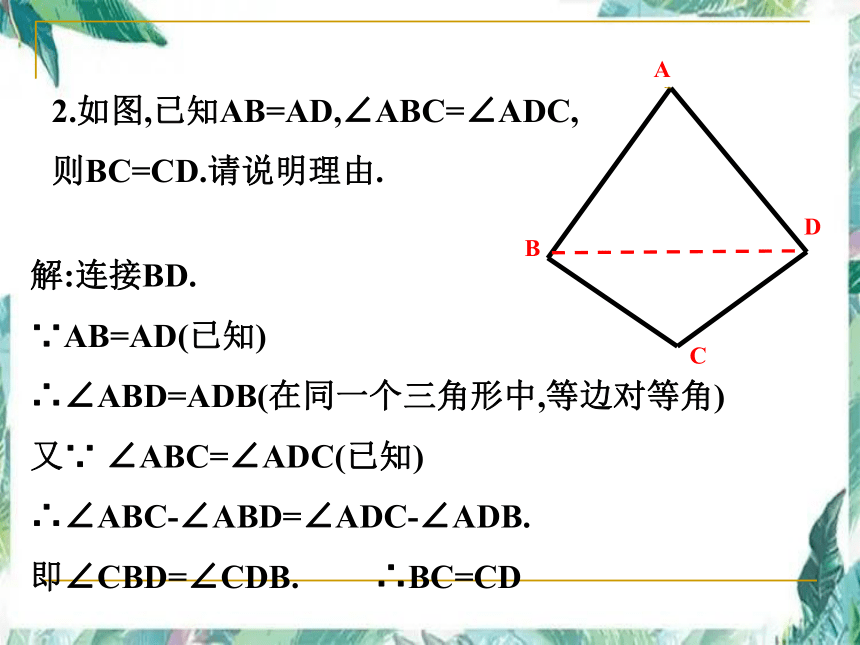
2.如图,已知AB=AD,∠ABC=∠ADC,
则BC=CD.请说明理由.
A
B
C
D
解:连接BD.
∵AB=AD(已知)
∴∠ABD=ADB(在同一个三角形中,等边对等角)
又∵ ∠ABC=∠ADC(已知)
∴∠ABC-∠ABD=∠ADC-∠ADB.
即∠CBD=∠CDB. ∴BC=CD
变式训练:若C点为三角形ABD内一点时,其他条件不变,原结论仍然成立吗
如图,已知AB=AD,∠ABC=∠ADC, 则BC=CD.请说明理由.
A
B
C
D
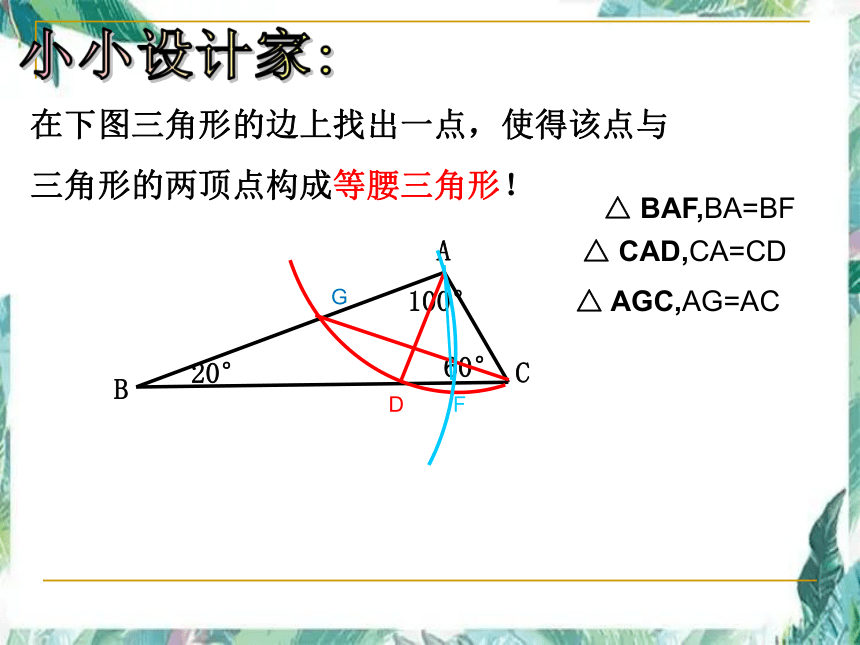
在下图三角形的边上找出一点,使得该点与
三角形的两顶点构成等腰三角形!
B
A
C
60°
100°
20°
△ CAD,CA=CD
△ BAF,BA=BF
△ AGC,AG=AC
D
G
F
在下图三角形的边上找出一点,使得该点与
三角形的两顶点构成等腰三角形!
B
A
C
60°
100°
20°
△ CAD,CA=CD
△ BAF,BA=BF
△ AGC,AG=AC
D
G
F
H
△ HAB,HA=HB
△ GBC,GB=GC
△ CAD是等边三角形
在下图三角形的边上找出一点,使得该点与
三角形的两顶点构成等腰三角形!
B
A
C
60°
100°
20°
△ CAD,CA=CD
△ BAF,BA=BF
△ AGC,AG=AC
D
G
F
H
△ HAB,HA=HB
△ GBC,GB=GC
△ CAD是等边三角形
驶向胜利的彼岸
本节课所学内容是:
1.等腰三角形的判定定理;
2.证明等腰三角形判定定理添加辅助线的方法是两种:高线与角平分线;
3.等腰三角形的判定定理与性质定理的区别与联系;
4.请对本节课的收获做出自己的评价。
作业:
1、完成课后练习第3题,P82习题第5、6题
2、预习等边三角形。
兵马俑坑至今已出土清理各种陶俑1000多尊,除跪射俑外,皆有不同程度的损坏,需要人工修复。而这尊跪射俑是保存最完整的、惟一一尊未经人工修复的。仔细观察,就连衣纹、发丝都还清晰可见。跪射俑何以能保存得如此完整?这得益于它的低姿态。首先,兵马俑坑都是地下道式土木结构建筑,当棚顶塌陷、土木俱下时,高大的立姿俑首当其冲,低姿的跪射俑受损害就小一些。其次,跪射俑作蹲跪姿,右膝、右足、左足三个支点呈等腰三角形支撑着上体,重心在下,增强了稳定性,与两足站立的立姿俑相比,不容易倾倒、破碎。因此,在经历了两千年的岁月风霜后,它依然能完整地呈现在我们面前。
等腰三角形性质与判定的对比
名称 图 形 概 念 性质 判 定
等
腰
三
角
形
A
B
C
有两边相等的三角形是等腰三角形
2.等边对等角
3. 三线合一
4.是轴对称图形
2.等角对等边
1.两边相等
1.两腰相等
运用等腰三角形的判定定理时,应注意在同一个三角形中.
解:
∴ ∠B=∠DAC —∠C
=60°—30°=30°
∵∠DAC=∠B+∠C
∴ ∠B=∠C
∴ AB=AC
即AC的长度就是河的宽度AB的长度
3.测量河宽AB,小聪从点A出发,沿着与直线AB成60°角的AC方向前进至C,在C处测得∠C=30°, 量出AC的长,它就是河的宽度这个方法正确吗?请说明理由。
C
A
D
60
30°
B
在下图三角形的边上找出一点,使得该点与
三角形的两顶点构成等腰三角形!
B
A
C
D
△ CAD,CA=CD
F
△ BAF,BA=BF
G
△ AGC,AG=AC
一变:如图,BD是等腰三角形ABC的底角∠ ABC的角平分线,DE∥BC,交AB于点E。判断△ BDE是不是等腰三角形,并说明理由。
如图,BD是∠ ABC的角平分线,DE∥BC,交AB于点E。判断△ BDE是不是等腰三角形,并说明理由。
B
C
D
E
A
二变:在△ABC中,已知 AB =AC ,BO平分∠ABC,
CO平分∠ACB
③猜想线段DE和线段DB,EC之间的关系 并说明理由。
B
O
C
A
D
E
DE=DB+CE
也可得:DE=2DB=2CE
②过点O作DE∥BC,则图中有 个等腰三角形。
①则△ OBC是 三角形
等腰
5
O
A
B
如图,位于海上A、B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B。如果这两艘救生船以同样的速度同时出发,能不能同时赶到出事地点(不考虑风浪因素)?
问题情境 :
A
C
B
D
A
A
B
B
D
D
C
C
1
2
AD⊥BC
AD平分∠BAC
BD=CD
O
A
B
思考:如图,位于海上A、B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B。如果这两艘救生船以同样的速度同时出发,能不能同时赶到出事地点(不考虑风浪因素)?
② 在图中,可得线段关系是 ( )
A、 DE=BD+EC
B、 DE>BD+EC
C、 DE<BD+EC
D、 无法确定
三变:如果△ ABC不是等腰三角形, ∠ABC和∠ACB的角平分线相交于点O, DE∥BC。
2
A
C
B
O
E
D
A
① 则图中等腰三角形共有 个。
1、如图,∠A=36°,∠DBC=36°,∠C=72°。分别计算∠1、∠2的度数,并说明图中有哪些等腰三角形。
2、如图,把一张矩形的纸沿对角线折叠,重合部分是一个等腰三角形吗?
3、如图,AC和BD相交于点O,且AB∥DC,OA=OB。
求证:OC=OD。
A
B
C
D
E
1、等腰三角形是怎样定义的?
有两条边相等的三角形,叫做等腰三角形。
①等腰三角形是轴对称图形。
③等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称为“三线合一”).
②等腰三角形的两个底角相等(简写成“等边对等角”) 。
2、等腰三角形有哪些性质?
D
A
B
C
既是性质又是判定
2.如图,在△ABC中,D、E分别是AB、
AC上的点,DE∥BC,∠1= ∠2。
说明△ABC的等腰三角形的理由.
1. 已知一个三角形的两个角的度数分别为43°,94°,
这个三角形是等腰三角形吗?
例1 一次数学实践活动的内容是测量河宽,如图,即测量A,B之间的距离.同学们想出了许多方法,其中小聪的方法是:从点A出发,沿着与直线AB成60°角的AC方向前进至C,在C处测得∠C=30°.量出AC的长,它就是河的宽度AB(即A,B之间的距离).这个方法正确吗?请说明理由.
A
B
C
30O
60O
D
已知,如图,在△ABC中,∠C=30° ,外角∠DAC=60°.则AB=AC,请说明理由.
A
B
C
30O
60O
实际问题
数学问题
D
1.如图,上午8时,一艘船从A处出发以15海里/时的速度向正北方向航行,9时45分到达B处.从A处测得灯塔C在北偏西26°方向,从B处测得灯塔C在北偏西52°方向,求B处到灯塔C的距离.
A
B
C
E
北
26°
52°
如图,BD是等腰三角形ABC的底边AC上的高,
DE BC,交AB于点E.
判断 BDE是不是等腰三角形,请说明理由。
A
E
D
B
C
1
2
3
1.等腰三角形△ABC中,∠A的外角是110°,则∠B= .
2.如图,AB=AC,BD平分∠ABC,且∠C=2∠A,
则图中等腰三角形共有 个.
A
B
C
D
4.已知∠EAC是△ABC的外角,∠1=∠2,AD∥BC,请说明AB=AC的理由.
A
B
C
D
E
1
2
3.AB=AC,BF 平分∠ABC交AC于F,CE平分∠ACB交AB于E,BF和BE交于点D,且EF∥BC,则图中有 个等腰三角形.
6
70°或 55°
3
5.如图,在△ABC中,D、E分别是AC、AB上的点,BD、CE交于点O。若∠BEO= ∠CDO,BE=CD。
问△ABC是等腰三角形吗?请说明理由.
4.已知∠EAC是△ABC的外角,∠1=∠2,AD∥BC,请说明AB=AC的理由.
A
B
C
D
E
1
2
在同一个三角形中,等角对等边.
本节课我们学习了什么内容?
名称 图 形 概 念 性质与边角关系 判 定
等
腰
三
角
形
A
B
C
有两边相等的三角形是等腰三角形
2.等边对等角
3. 三线合一
4.是轴对称图形
2.等角对等边
1.两边相等
1.两腰相等
解析:要证BC=CD,若连接AC证△ABC≌△ADC,发现条件不够.
因此可以考虑连接BD,只需证∠CBD=∠CDB,而由已知条件知∠ABD=∠ADB, ∠ABC=∠ADC, 从而∠CBD=∠CDB
2.如图,已知AB=AD,∠ABC=∠ADC, 则BC=CD.请说明理由.
A
B
C
D
解:连接BD.
∵AB=AD(已知)
∴∠ABD=ADB(在同一个三角形中,等边对等角)
又∵ ∠ABC=∠ADC(已知)
∴∠ABC-∠ABD=∠ADC-∠ADB.
即∠CBD=∠CDB. ∴BC=CD
想一想:若C点为三角形ABD内一点时,其他条件不变,原结论仍然成立吗
如图,已知AB=AD,∠ABC=∠ADC, 则BC=CD.请说明理由.
A
B
C
D
大显身手
如图,在△ABC中,AB=AC,∠ABC和∠ACB的平分线交于点O.过O作EF∥BC交AB于E,交AC于F.
(1)、请你写出图中所有等腰三角形,并探究EF、BE、FC之间的关系;
∴∠2=∠ABO ∠3=∠ACO
O
A
B
C
E
F
若AB≠AC,其他条件不变,图中还有等腰三角形吗?(1)中结论还成立吗?
解:
EF=BE+CF
理由:
A
B
C
O
E
F
1
3
2
4
∵ EF∥BC
∴∠1=∠2 ∠3=∠4
∵ BO、CO分别平分∠ABC、∠ACB
∴∠1=∠ABO ∠4=∠ACO
∴BE=OE CF=OF
∵ EF=EO+FO
∴EF=BE+CF
学习目标:
1. 掌握等腰三角形的判定定理.
2、会综合运用等腰三角形的性质和判定进行有关的计算和证明。
3、理解等腰三角形性质定理和判定定理的区别。
重点
难点
重点
自学课本P89---90,并完成学案----自主学习
把“等腰三角形的两个底角相等”改写成“如果------那么-----”形式。
逆命题:
如果一个三角形有两个角相等,那么这个三角形是等腰三角形.
如果一个三角形是等腰三角形,那么这个三角形的两个底角相等.
它是真命题吗
1、如图,把一张矩形的纸沿对角线折叠,重合部分是一个等腰三角形吗?说明理由。
A
B
C
D
E
2、如图,AB=AC,∠A=36°BD平分∠ABC交AC于点D.图中有哪些等腰三角形。选择一个说明理由。
反馈矫正
在下图三角形的边上找出一点,使得该点与
三角形的两顶点构成等腰三角形!
过C作∠BCD=20°,并交AB与点D,
D
△BCD是等腰三角形吗?
猜想:如果一个三角形有两个角相等,那么这个三角形是等腰三角形。
B
A
C
60°
100°
20°
如果一个三角形有两个角相等,
那么这个三角形是等腰三角形。
这又是一个判定两条线段相等根据之一.
用几何语言表示为:
在△ABC中,
∵∠B=∠C ( 已知 )
∴ AC=AB. ( )
在一个三角形中,等角对等边
等腰三角形的判定定理:
简单地说,在同一个三角形中,等角对等边。
A
B
C
例1:如图,上午10 时,一条船从A处出发以20海里每小时的速度向正北航行,中午12时到达B处,从A、B望灯塔C,测得∠NAC=40°∠NBC=80°求从B处到灯塔C的距离
解:∵∠NBC=∠A+∠C
∴∠C=80°- 40°= 40°
∴ ∠C = ∠A
∴ BA=BC(等角对等边)
∵AB=20(12-10)=40
∴BC=40
答:B处到达灯塔C40海里
小试牛刀
80°
40°
N
B
A
C
北
19.4.2 等腰三角形的判定
思考:“等腰三角形的两个底角相等”的逆命题是什么?
逆命题:
如果一个三角形有两个角相等,那么这两
个角所对的边也相等
探究新知
● 操作一
做一做
你发现了什么结论?其他同学的结果与你的相同吗?
● 操作二
量一量,线段AB与AC的长度。
画△ABC.使∠B=∠C=30°
活动一:
A
B
C
D
1
2
已知:如图,在ΔABC中,∠B=∠C。
求证:AB=AC
证明:
作∠BAC的平分线AD
∵ AD平分∠BAC
∴ ∠1=∠2
在△BAD和△CAD中
如果一个三角形有两个角相等,那么这两
个角所对的边也相等
∠B=∠C
∠1=∠2
AD=AD (公共边)
∴ AB= AC (全等三角形的对应边相等)
∴ △BAD ≌ △CAD (AAS)
活动三:
A
B
C
D
已知:如图,在ΔABC中,∠B=∠C。
求证:AB=AC
证明:
作AD⊥BC
∵ AD ⊥BC
∴∠ADB=∠ADC=90°
在△BAD和△CAD中
如果一个三角形有两个角相等,那么这两
个角所对的边也相等
∠B=∠C
AD=AD (公共边)
∴ AB= AC (全等三角形的对应边相等)
∴ △BAD ≌ △CAD (AAS)
∠ADB=∠ADC
活动三:
A
B
C
D
已知:如图,在ΔABC中,∠B=∠C。
求证:AB=AC
如果一个三角形有两个角相等,那么这两
个角所对的边也相等
活动三:
证明:
作BC边上的中线AD
A
B
C
如果一个三角形有两个角相等,那么这两个角所对的边也相等
几何语言:
∵∠B =∠C (已知)
∴ AB=AC(等角对等边)
等腰三角形的判定定理:
(简写成“等角对等边”)。
例题.如图,AD平分△ABC的外角∠EAC,AD//BC,则△ ABC是等腰三角形吗?说明你的理由。
证明:∵AD∥BC,
A
E
B
C
1
2
D
∴∠1=∠B(两直线平行,同位角相等)
∠2=∠C(两直线平行,内错角相等)
∵ ∠1=∠2,
∴∠B=∠C
∴AB=AC(等角对等边)
活动四:
巩固新知:1. 下列两个图形是否是等腰三角形?
750
300
400
400
2.如图,已知AB=AD,∠ABC=∠ADC,
则BC=CD.请说明理由.
A
B
C
D
解:连接BD.
∵AB=AD(已知)
∴∠ABD=ADB(在同一个三角形中,等边对等角)
又∵ ∠ABC=∠ADC(已知)
∴∠ABC-∠ABD=∠ADC-∠ADB.
即∠CBD=∠CDB. ∴BC=CD
变式训练:若C点为三角形ABD内一点时,其他条件不变,原结论仍然成立吗
如图,已知AB=AD,∠ABC=∠ADC, 则BC=CD.请说明理由.
A
B
C
D
在下图三角形的边上找出一点,使得该点与
三角形的两顶点构成等腰三角形!
B
A
C
60°
100°
20°
△ CAD,CA=CD
△ BAF,BA=BF
△ AGC,AG=AC
D
G
F
在下图三角形的边上找出一点,使得该点与
三角形的两顶点构成等腰三角形!
B
A
C
60°
100°
20°
△ CAD,CA=CD
△ BAF,BA=BF
△ AGC,AG=AC
D
G
F
H
△ HAB,HA=HB
△ GBC,GB=GC
△ CAD是等边三角形
在下图三角形的边上找出一点,使得该点与
三角形的两顶点构成等腰三角形!
B
A
C
60°
100°
20°
△ CAD,CA=CD
△ BAF,BA=BF
△ AGC,AG=AC
D
G
F
H
△ HAB,HA=HB
△ GBC,GB=GC
△ CAD是等边三角形
驶向胜利的彼岸
本节课所学内容是:
1.等腰三角形的判定定理;
2.证明等腰三角形判定定理添加辅助线的方法是两种:高线与角平分线;
3.等腰三角形的判定定理与性质定理的区别与联系;
4.请对本节课的收获做出自己的评价。
作业:
1、完成课后练习第3题,P82习题第5、6题
2、预习等边三角形。
兵马俑坑至今已出土清理各种陶俑1000多尊,除跪射俑外,皆有不同程度的损坏,需要人工修复。而这尊跪射俑是保存最完整的、惟一一尊未经人工修复的。仔细观察,就连衣纹、发丝都还清晰可见。跪射俑何以能保存得如此完整?这得益于它的低姿态。首先,兵马俑坑都是地下道式土木结构建筑,当棚顶塌陷、土木俱下时,高大的立姿俑首当其冲,低姿的跪射俑受损害就小一些。其次,跪射俑作蹲跪姿,右膝、右足、左足三个支点呈等腰三角形支撑着上体,重心在下,增强了稳定性,与两足站立的立姿俑相比,不容易倾倒、破碎。因此,在经历了两千年的岁月风霜后,它依然能完整地呈现在我们面前。
等腰三角形性质与判定的对比
名称 图 形 概 念 性质 判 定
等
腰
三
角
形
A
B
C
有两边相等的三角形是等腰三角形
2.等边对等角
3. 三线合一
4.是轴对称图形
2.等角对等边
1.两边相等
1.两腰相等
运用等腰三角形的判定定理时,应注意在同一个三角形中.
解:
∴ ∠B=∠DAC —∠C
=60°—30°=30°
∵∠DAC=∠B+∠C
∴ ∠B=∠C
∴ AB=AC
即AC的长度就是河的宽度AB的长度
3.测量河宽AB,小聪从点A出发,沿着与直线AB成60°角的AC方向前进至C,在C处测得∠C=30°, 量出AC的长,它就是河的宽度这个方法正确吗?请说明理由。
C
A
D
60
30°
B
在下图三角形的边上找出一点,使得该点与
三角形的两顶点构成等腰三角形!
B
A
C
D
△ CAD,CA=CD
F
△ BAF,BA=BF
G
△ AGC,AG=AC
一变:如图,BD是等腰三角形ABC的底角∠ ABC的角平分线,DE∥BC,交AB于点E。判断△ BDE是不是等腰三角形,并说明理由。
如图,BD是∠ ABC的角平分线,DE∥BC,交AB于点E。判断△ BDE是不是等腰三角形,并说明理由。
B
C
D
E
A
二变:在△ABC中,已知 AB =AC ,BO平分∠ABC,
CO平分∠ACB
③猜想线段DE和线段DB,EC之间的关系 并说明理由。
B
O
C
A
D
E
DE=DB+CE
也可得:DE=2DB=2CE
②过点O作DE∥BC,则图中有 个等腰三角形。
①则△ OBC是 三角形
等腰
5
O
A
B
如图,位于海上A、B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B。如果这两艘救生船以同样的速度同时出发,能不能同时赶到出事地点(不考虑风浪因素)?
问题情境 :
A
C
B
D
A
A
B
B
D
D
C
C
1
2
AD⊥BC
AD平分∠BAC
BD=CD
O
A
B
思考:如图,位于海上A、B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B。如果这两艘救生船以同样的速度同时出发,能不能同时赶到出事地点(不考虑风浪因素)?
② 在图中,可得线段关系是 ( )
A、 DE=BD+EC
B、 DE>BD+EC
C、 DE<BD+EC
D、 无法确定
三变:如果△ ABC不是等腰三角形, ∠ABC和∠ACB的角平分线相交于点O, DE∥BC。
2
A
C
B
O
E
D
A
① 则图中等腰三角形共有 个。
1、如图,∠A=36°,∠DBC=36°,∠C=72°。分别计算∠1、∠2的度数,并说明图中有哪些等腰三角形。
2、如图,把一张矩形的纸沿对角线折叠,重合部分是一个等腰三角形吗?
3、如图,AC和BD相交于点O,且AB∥DC,OA=OB。
求证:OC=OD。
A
B
C
D
E
1、等腰三角形是怎样定义的?
有两条边相等的三角形,叫做等腰三角形。
①等腰三角形是轴对称图形。
③等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称为“三线合一”).
②等腰三角形的两个底角相等(简写成“等边对等角”) 。
2、等腰三角形有哪些性质?
D
A
B
C
既是性质又是判定
2.如图,在△ABC中,D、E分别是AB、
AC上的点,DE∥BC,∠1= ∠2。
说明△ABC的等腰三角形的理由.
1. 已知一个三角形的两个角的度数分别为43°,94°,
这个三角形是等腰三角形吗?
例1 一次数学实践活动的内容是测量河宽,如图,即测量A,B之间的距离.同学们想出了许多方法,其中小聪的方法是:从点A出发,沿着与直线AB成60°角的AC方向前进至C,在C处测得∠C=30°.量出AC的长,它就是河的宽度AB(即A,B之间的距离).这个方法正确吗?请说明理由.
A
B
C
30O
60O
D
已知,如图,在△ABC中,∠C=30° ,外角∠DAC=60°.则AB=AC,请说明理由.
A
B
C
30O
60O
实际问题
数学问题
D
1.如图,上午8时,一艘船从A处出发以15海里/时的速度向正北方向航行,9时45分到达B处.从A处测得灯塔C在北偏西26°方向,从B处测得灯塔C在北偏西52°方向,求B处到灯塔C的距离.
A
B
C
E
北
26°
52°
如图,BD是等腰三角形ABC的底边AC上的高,
DE BC,交AB于点E.
判断 BDE是不是等腰三角形,请说明理由。
A
E
D
B
C
1
2
3
1.等腰三角形△ABC中,∠A的外角是110°,则∠B= .
2.如图,AB=AC,BD平分∠ABC,且∠C=2∠A,
则图中等腰三角形共有 个.
A
B
C
D
4.已知∠EAC是△ABC的外角,∠1=∠2,AD∥BC,请说明AB=AC的理由.
A
B
C
D
E
1
2
3.AB=AC,BF 平分∠ABC交AC于F,CE平分∠ACB交AB于E,BF和BE交于点D,且EF∥BC,则图中有 个等腰三角形.
6
70°或 55°
3
5.如图,在△ABC中,D、E分别是AC、AB上的点,BD、CE交于点O。若∠BEO= ∠CDO,BE=CD。
问△ABC是等腰三角形吗?请说明理由.
4.已知∠EAC是△ABC的外角,∠1=∠2,AD∥BC,请说明AB=AC的理由.
A
B
C
D
E
1
2
在同一个三角形中,等角对等边.
本节课我们学习了什么内容?
名称 图 形 概 念 性质与边角关系 判 定
等
腰
三
角
形
A
B
C
有两边相等的三角形是等腰三角形
2.等边对等角
3. 三线合一
4.是轴对称图形
2.等角对等边
1.两边相等
1.两腰相等
解析:要证BC=CD,若连接AC证△ABC≌△ADC,发现条件不够.
因此可以考虑连接BD,只需证∠CBD=∠CDB,而由已知条件知∠ABD=∠ADB, ∠ABC=∠ADC, 从而∠CBD=∠CDB
2.如图,已知AB=AD,∠ABC=∠ADC, 则BC=CD.请说明理由.
A
B
C
D
解:连接BD.
∵AB=AD(已知)
∴∠ABD=ADB(在同一个三角形中,等边对等角)
又∵ ∠ABC=∠ADC(已知)
∴∠ABC-∠ABD=∠ADC-∠ADB.
即∠CBD=∠CDB. ∴BC=CD
想一想:若C点为三角形ABD内一点时,其他条件不变,原结论仍然成立吗
如图,已知AB=AD,∠ABC=∠ADC, 则BC=CD.请说明理由.
A
B
C
D
大显身手
如图,在△ABC中,AB=AC,∠ABC和∠ACB的平分线交于点O.过O作EF∥BC交AB于E,交AC于F.
(1)、请你写出图中所有等腰三角形,并探究EF、BE、FC之间的关系;
∴∠2=∠ABO ∠3=∠ACO
O
A
B
C
E
F
若AB≠AC,其他条件不变,图中还有等腰三角形吗?(1)中结论还成立吗?
解:
EF=BE+CF
理由:
A
B
C
O
E
F
1
3
2
4
∵ EF∥BC
∴∠1=∠2 ∠3=∠4
∵ BO、CO分别平分∠ABC、∠ACB
∴∠1=∠ABO ∠4=∠ACO
∴BE=OE CF=OF
∵ EF=EO+FO
∴EF=BE+CF
学习目标:
1. 掌握等腰三角形的判定定理.
2、会综合运用等腰三角形的性质和判定进行有关的计算和证明。
3、理解等腰三角形性质定理和判定定理的区别。
重点
难点
重点
自学课本P89---90,并完成学案----自主学习
把“等腰三角形的两个底角相等”改写成“如果------那么-----”形式。
逆命题:
如果一个三角形有两个角相等,那么这个三角形是等腰三角形.
如果一个三角形是等腰三角形,那么这个三角形的两个底角相等.
它是真命题吗
1、如图,把一张矩形的纸沿对角线折叠,重合部分是一个等腰三角形吗?说明理由。
A
B
C
D
E
2、如图,AB=AC,∠A=36°BD平分∠ABC交AC于点D.图中有哪些等腰三角形。选择一个说明理由。
反馈矫正
在下图三角形的边上找出一点,使得该点与
三角形的两顶点构成等腰三角形!
过C作∠BCD=20°,并交AB与点D,
D
△BCD是等腰三角形吗?
猜想:如果一个三角形有两个角相等,那么这个三角形是等腰三角形。
B
A
C
60°
100°
20°
如果一个三角形有两个角相等,
那么这个三角形是等腰三角形。
这又是一个判定两条线段相等根据之一.
用几何语言表示为:
在△ABC中,
∵∠B=∠C ( 已知 )
∴ AC=AB. ( )
在一个三角形中,等角对等边
等腰三角形的判定定理:
简单地说,在同一个三角形中,等角对等边。
A
B
C
例1:如图,上午10 时,一条船从A处出发以20海里每小时的速度向正北航行,中午12时到达B处,从A、B望灯塔C,测得∠NAC=40°∠NBC=80°求从B处到灯塔C的距离
解:∵∠NBC=∠A+∠C
∴∠C=80°- 40°= 40°
∴ ∠C = ∠A
∴ BA=BC(等角对等边)
∵AB=20(12-10)=40
∴BC=40
答:B处到达灯塔C40海里
小试牛刀
80°
40°
N
B
A
C
北
