冀教版八年级上册17.3 勾股定理课件(共25张PPT)
文档属性
| 名称 | 冀教版八年级上册17.3 勾股定理课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 890.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-04 08:41:31 | ||
图片预览


文档简介
(共25张PPT)
17.3 勾股定理(通用)
第一关观察猜想
数学家毕达哥拉斯
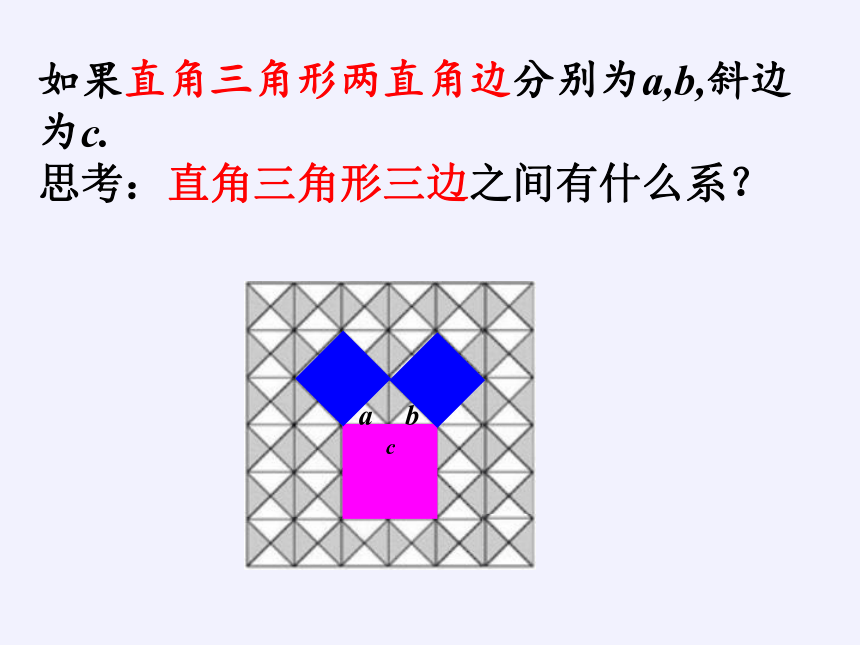
如果直角三角形两直角边分别为a,b,斜边为c.
思考:直角三角形三边之间有什么系?
a
b
c
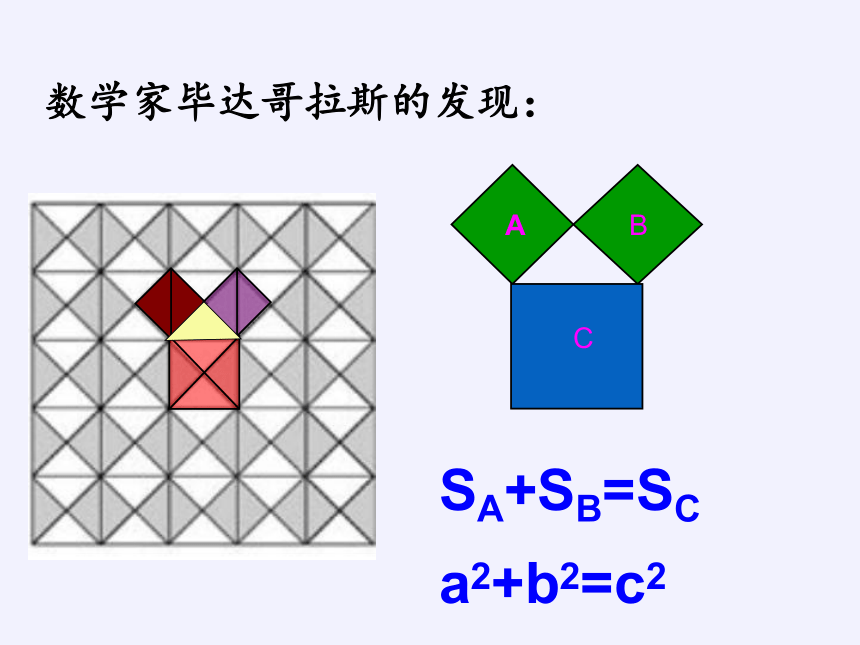
数学家毕达哥拉斯的发现:
A
B
C
SA+SB=SC
a2+b2=c2
C
A
B
a
b
c
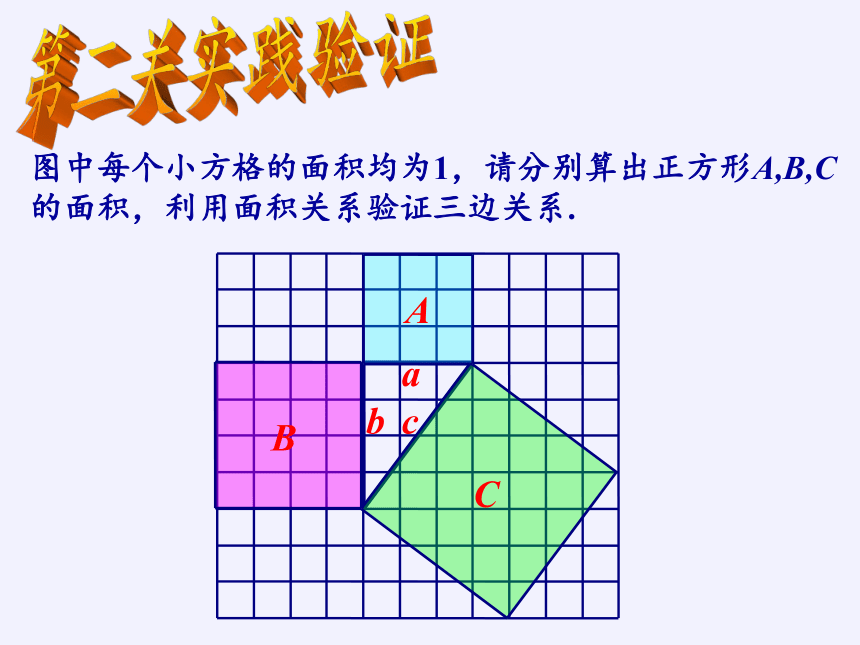
第二关实践验证
图中每个小方格的面积均为1,请分别算出正方形A,B,C 的面积,利用面积关系验证三边关系.
P
Q
C
R
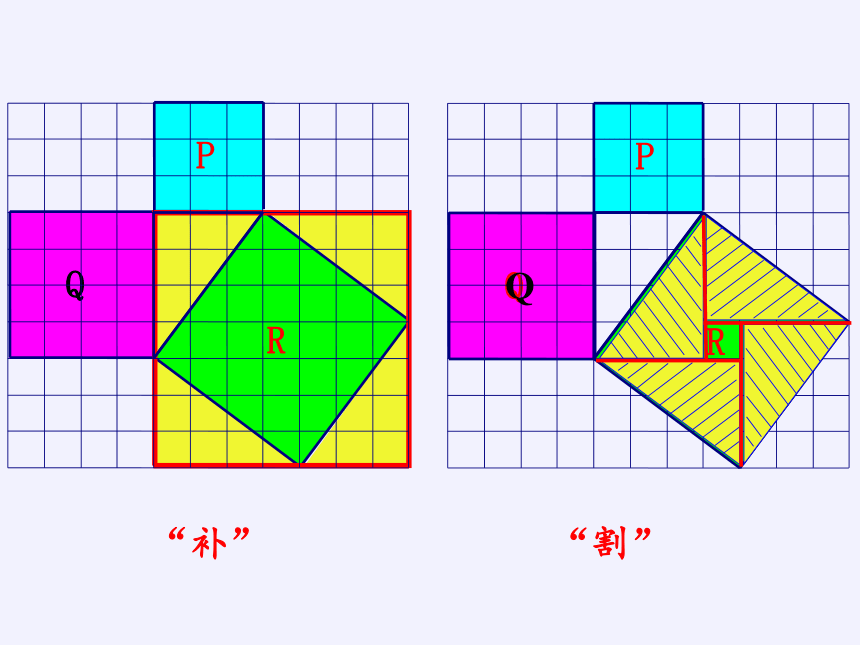
“补”
P
Q
C
R
“割”
Q
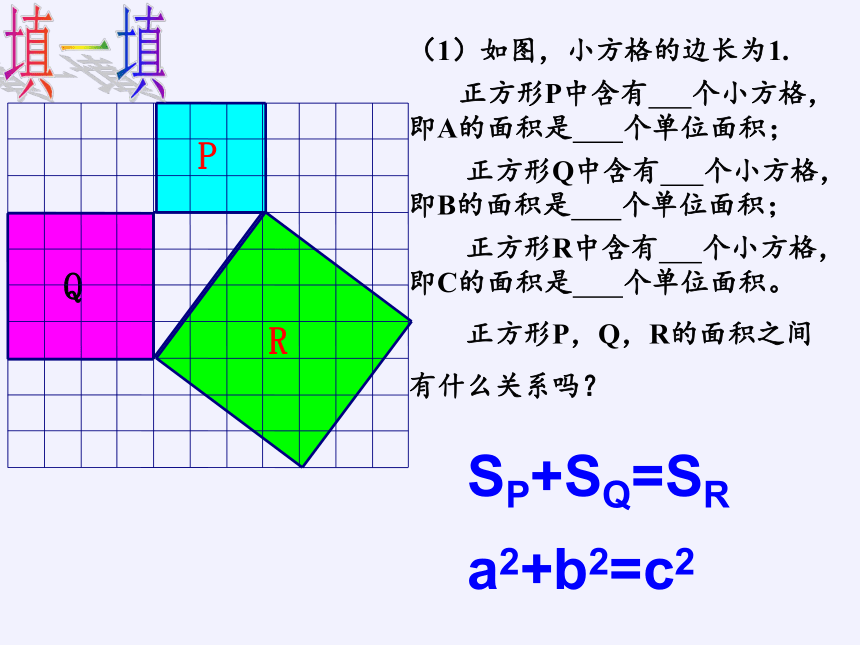
(1)如图,小方格的边长为1.
正方形P中含有 个小方格,即A的面积是 个单位面积;
正方形Q中含有 个小方格,即B的面积是 个单位面积;
正方形R中含有 个小方格,即C的面积是 个单位面积。
正方形P,Q,R的面积之间
有什么关系吗?
R
P
Q
填一填
SP+SQ=SR
a2+b2=c2
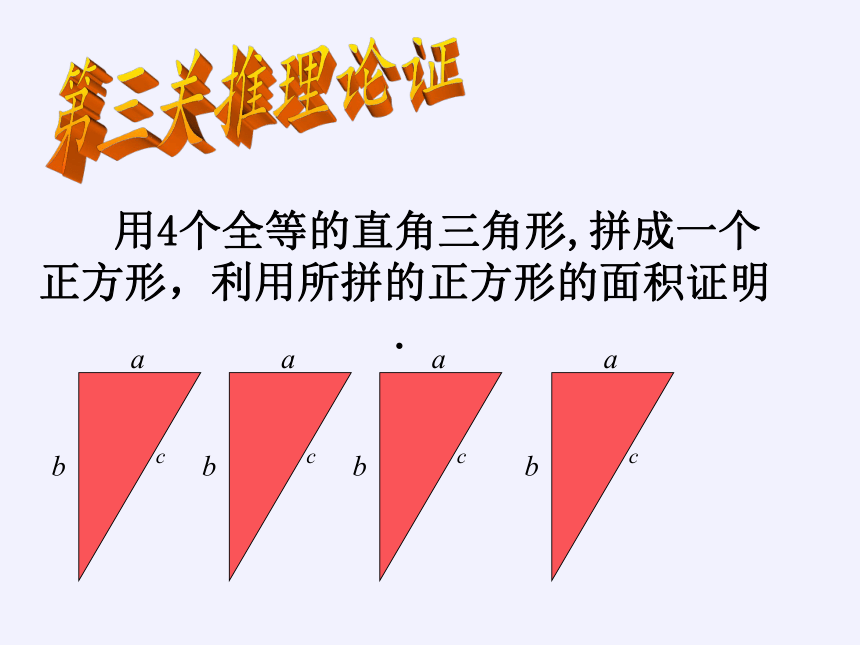
第三关推理论证
用4个全等的直角三角形,拼成一个正方形,利用所拼的正方形的面积证明.
a
b
c
a
b
c
a
b
c
a
b
c
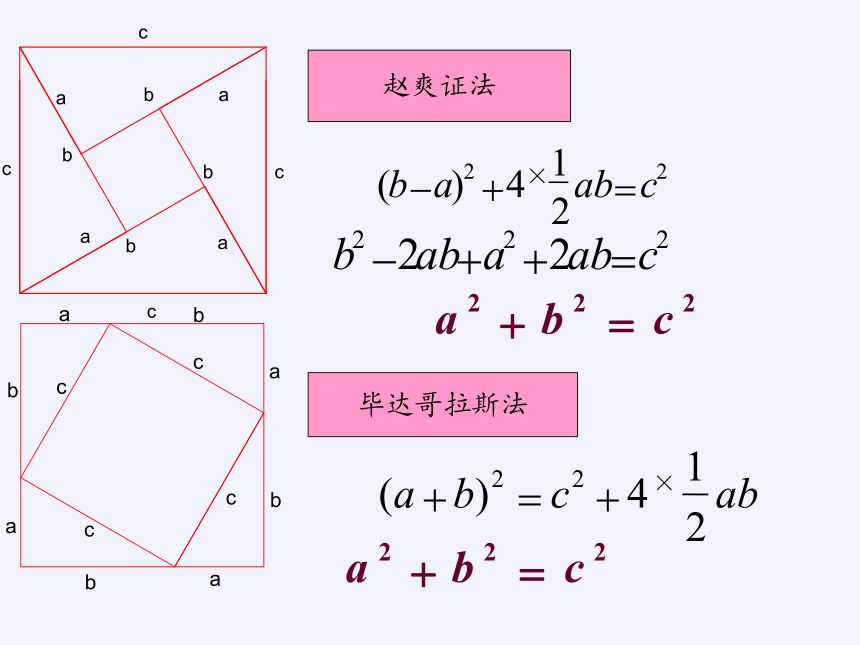
赵爽证法
毕达哥拉斯法
2
2
2
1
4
)
(
c
ab
a
b
=
×
+
-
2
2
2
2
2
c
ab
a
ab
b
=
+
+
-
2
2
2
c
b
a
=
+
ab
c
b
a
2
1
4
)
(
2
2
×
+
=
+
2
2
2
c
b
a
=
+
勾股定理
如果直角三角形两直角边分别为a,b,斜边为c,那么
a
b
c
a2 + b2 = c2
即直角三角形两直角边的平方和等于斜边的平方.
解决问题
1m
2m
A
D
C
B
一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过 为什么?
解决问题
1 一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过 为什么?
2m
A
D
C
B
1m
解:连结AC,在Rt△AB中,∠B=90°,根据勾股定理:
AC2 = AB2+BC2= 12+22 =5
∴ AC=
答:薄木板能从门框内通过。
>2.2m
请你求出下列图中未知数的值:
x
81
144
⑴
169
144
y
⑵
625
576
z
⑶
试一试
图中,所有的四边形都是正方形,所有的三角形都是直角三角形,正方形M,N的面积的和是_____.
100
M
N
A
B
C
D
感受数学之美
100
在直线上依次摆着7个正方形(如图),已知倾斜放置的3个正方形的面积分别为1,2,3,水平放置的4个正方形的面积是S1,S2,S3,S4,则S1+S2+S3+S4=______.
能力提升
意大利文艺复兴时代的著名画家达芬奇也深深的沉醉在勾股定理的魅力中。
勾股趣话
美国第二十任总统伽菲尔德巧证勾股定理--称为“总统”证法
勾股趣话
a
D
b
C
c
a
b
c
A
B
E
1955年希腊曾发行了一枚纪念邮票
与外星人沟通的“勾股定理”图标
一种思想
数形结合
一份反思
身为中国人
勾股定理
一个定理
特殊到一般
一次探索
收获
2、查阅有关勾股定理的历史资料.
作业
1、教材习题,第1、2、3题;
如图,你能求出S1、S2、S3之间的关系式吗?
S1
S3
S2
课外思考
以直角三角形三边为边作等边三角形,这3个等边三角形 的面积之间有什么关系?
A
B
C
D
E
F
课外思考
谢 谢
17.3 勾股定理(通用)
第一关观察猜想
数学家毕达哥拉斯
如果直角三角形两直角边分别为a,b,斜边为c.
思考:直角三角形三边之间有什么系?
a
b
c
数学家毕达哥拉斯的发现:
A
B
C
SA+SB=SC
a2+b2=c2
C
A
B
a
b
c
第二关实践验证
图中每个小方格的面积均为1,请分别算出正方形A,B,C 的面积,利用面积关系验证三边关系.
P
Q
C
R
“补”
P
Q
C
R
“割”
Q
(1)如图,小方格的边长为1.
正方形P中含有 个小方格,即A的面积是 个单位面积;
正方形Q中含有 个小方格,即B的面积是 个单位面积;
正方形R中含有 个小方格,即C的面积是 个单位面积。
正方形P,Q,R的面积之间
有什么关系吗?
R
P
Q
填一填
SP+SQ=SR
a2+b2=c2
第三关推理论证
用4个全等的直角三角形,拼成一个正方形,利用所拼的正方形的面积证明.
a
b
c
a
b
c
a
b
c
a
b
c
赵爽证法
毕达哥拉斯法
2
2
2
1
4
)
(
c
ab
a
b
=
×
+
-
2
2
2
2
2
c
ab
a
ab
b
=
+
+
-
2
2
2
c
b
a
=
+
ab
c
b
a
2
1
4
)
(
2
2
×
+
=
+
2
2
2
c
b
a
=
+
勾股定理
如果直角三角形两直角边分别为a,b,斜边为c,那么
a
b
c
a2 + b2 = c2
即直角三角形两直角边的平方和等于斜边的平方.
解决问题
1m
2m
A
D
C
B
一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过 为什么?
解决问题
1 一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过 为什么?
2m
A
D
C
B
1m
解:连结AC,在Rt△AB中,∠B=90°,根据勾股定理:
AC2 = AB2+BC2= 12+22 =5
∴ AC=
答:薄木板能从门框内通过。
>2.2m
请你求出下列图中未知数的值:
x
81
144
⑴
169
144
y
⑵
625
576
z
⑶
试一试
图中,所有的四边形都是正方形,所有的三角形都是直角三角形,正方形M,N的面积的和是_____.
100
M
N
A
B
C
D
感受数学之美
100
在直线上依次摆着7个正方形(如图),已知倾斜放置的3个正方形的面积分别为1,2,3,水平放置的4个正方形的面积是S1,S2,S3,S4,则S1+S2+S3+S4=______.
能力提升
意大利文艺复兴时代的著名画家达芬奇也深深的沉醉在勾股定理的魅力中。
勾股趣话
美国第二十任总统伽菲尔德巧证勾股定理--称为“总统”证法
勾股趣话
a
D
b
C
c
a
b
c
A
B
E
1955年希腊曾发行了一枚纪念邮票
与外星人沟通的“勾股定理”图标
一种思想
数形结合
一份反思
身为中国人
勾股定理
一个定理
特殊到一般
一次探索
收获
2、查阅有关勾股定理的历史资料.
作业
1、教材习题,第1、2、3题;
如图,你能求出S1、S2、S3之间的关系式吗?
S1
S3
S2
课外思考
以直角三角形三边为边作等边三角形,这3个等边三角形 的面积之间有什么关系?
A
B
C
D
E
F
课外思考
谢 谢
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
