沪教版五年级上册数学4.3方程课件(共15张PPT)
文档属性
| 名称 | 沪教版五年级上册数学4.3方程课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 916.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-04 08:25:30 | ||
图片预览




文档简介
(共15张PPT)
标题文字添加
PART 01
方程1
方程:
含有未知数的等式叫方程。
等式:
表示两边相等关系的式子。
等式与方程之间的关系:
方程一定是等式;
但等式不一定是方程。
回顾:
1、判断下面的式子哪些是方程?
1、X+2>10
2、y÷5=20
3、20-6 = 14
4、8x=0.3
5、n-5m = 15
2、y÷5=20
4、8x=0.3
5、n-5m = 15
回顾:
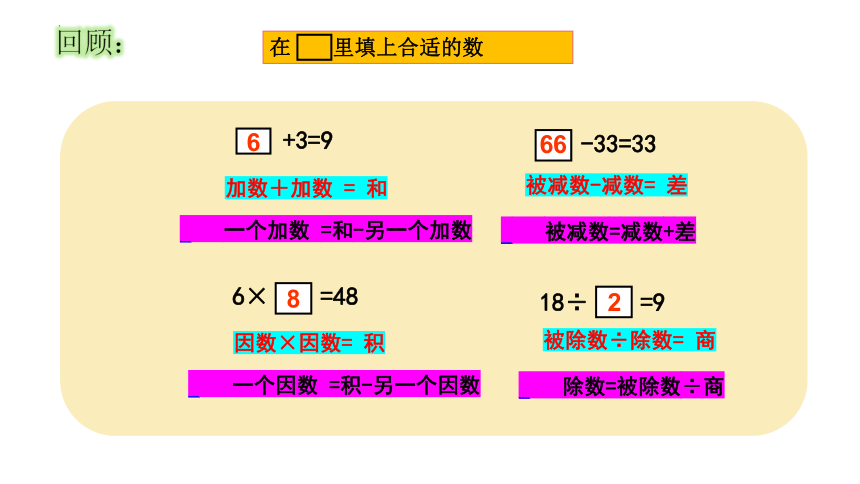
18÷ =9
6× =48
在 里填上合适的数
8
2
回顾:
-33=33
66
+3=9
6
加数+加数 = 和
一个加数 =和-另一个加数
被减数-减数= 差
被减数=减数+差
因数×因数= 积
一个因数 =积-另一个因数
被除数÷除数= 商
除数=被除数÷商
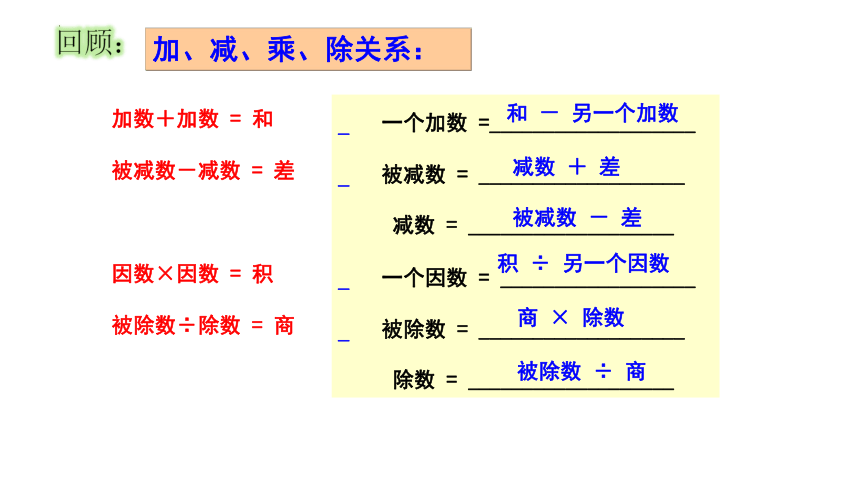
一个加数 =___________________
被减数 = ___________________
减数 = ___________________
一个因数 = __________________
被除数 = ___________________
除数 = ___________________
加数+加数 = 和
被减数-减数 = 差
因数×因数 = 积
被除数÷除数 = 商
和 - 另一个加数
减数 + 差
被减数 - 差
积 ÷ 另一个因数
商 × 除数
被除数 ÷ 商
加、减、乘、除关系:
回顾:
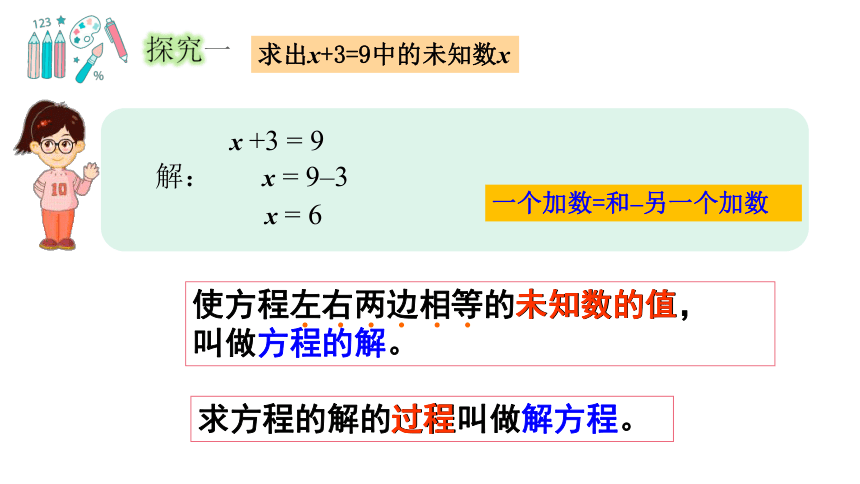
求出x+3=9中的未知数x
x +3 = 9
解: x = 9–3
x = 6
一个加数=和–另一个加数
探究一
求方程的解的过程叫做解方程。
过程
使方程左右两边相等的未知数的值,
叫做方程的解。
未知数的值
解方程:6x=19.8
6x = 19.8
解: x = 19.8÷6
x = 3.3
一个因数=积÷另一个因数
探究二
x=3.3是不是6x=19.8的解呢?
我们可以把x=3.3代入原方程6x=19.8 ,看看能不能使方程左右两边相等
检验:
把X=3.3代入原方程。
方程左边=6X=6 × 3.3=19.8,
方程右边=19.8。
因为左边=右边,
所以X=3.3是原方程的解。
解方程:x +3 = 9
探究二
x=6 是不是x+3=9的解呢?
检验:
把X=6代入原方程。
方程左边=x+3=6+3=9,
方程右边=9。
因为左边=右边,
所以X=6是原方程的解。
x +3 = 9
解: x = 9–3
x = 6
一个加数=和–另一个加数
解方程:6x=19.8
6x = 19.8
解: x = 19.8÷6
x = 3.3
探究二
x=3.3是不是6x=19.8的解呢?
检验:
把X=3.3代入原方程。
方程左边=6X=6 × 3.3=19.8,
方程右边=19.8。
因为左边=右边,
所以X=3.3是原方程的解。
解方程的格式要求:
解方程时先写“ 解:” 。
各行的等号要对齐。
想想未知数表示什么数,用到哪个关系式。
验算以“检验”的形式进行,有固定的格式。
没有书面检验要求的要进行口头检验,养成检验的好习惯。
X=13.8
检验:
把__________代入原方程。
方程左边=_____=______=_____,
方程右边=______。
因为_________,
所以________是原方程的解。
检验:
把X=46.8代入原方程。
方程左边=X÷6=46.8÷6=7.8,
方程右边=7.8。
因为左边=右边,
所以x=46.8是原方程的解。
X÷6=7.8
X=
X=
X=7.8 × 6
X=46.8
解:
7.8
6
13.8
+
X=13.8
X-6
13.8-6
7.8
7.8
左边=右边
解:
X – 6=7.8
比较两个方程的相同点和不同点?
巩固练习1
被减数=减数+差
被除数=商×除数
巩固练习2
练习册P59
X=7
检验:
把__________代入原方程。
方程左边=_____=______=_____,
方程右边=______。
因为_________,
所以________是原方程的解。
17.5÷x=2.5
X=
X=
X=17.5 ÷ 2.5
X=7
解:
15
8
7
-
X=7
15-x
15-7
8
8
左边=右边
解:
15 – x=8
巩固练习2
减数=被减数-差
除数=被除数÷商
练习册P59 B级
巩固练习3
小法官:判断
巩固练习4
回顾小结:
解方程的格式要求:
解方程时先写“ 解:” 。
各行的等号要对齐。
想想未知数表示什么数,用到哪个关系式。
验算以“检验”的形式进行,有固定的格式。
没有书面检验要求的要进行口头检验,养成检验的好习惯。
标题文字添加
PART 01
方程1
方程:
含有未知数的等式叫方程。
等式:
表示两边相等关系的式子。
等式与方程之间的关系:
方程一定是等式;
但等式不一定是方程。
回顾:
1、判断下面的式子哪些是方程?
1、X+2>10
2、y÷5=20
3、20-6 = 14
4、8x=0.3
5、n-5m = 15
2、y÷5=20
4、8x=0.3
5、n-5m = 15
回顾:
18÷ =9
6× =48
在 里填上合适的数
8
2
回顾:
-33=33
66
+3=9
6
加数+加数 = 和
一个加数 =和-另一个加数
被减数-减数= 差
被减数=减数+差
因数×因数= 积
一个因数 =积-另一个因数
被除数÷除数= 商
除数=被除数÷商
一个加数 =___________________
被减数 = ___________________
减数 = ___________________
一个因数 = __________________
被除数 = ___________________
除数 = ___________________
加数+加数 = 和
被减数-减数 = 差
因数×因数 = 积
被除数÷除数 = 商
和 - 另一个加数
减数 + 差
被减数 - 差
积 ÷ 另一个因数
商 × 除数
被除数 ÷ 商
加、减、乘、除关系:
回顾:
求出x+3=9中的未知数x
x +3 = 9
解: x = 9–3
x = 6
一个加数=和–另一个加数
探究一
求方程的解的过程叫做解方程。
过程
使方程左右两边相等的未知数的值,
叫做方程的解。
未知数的值
解方程:6x=19.8
6x = 19.8
解: x = 19.8÷6
x = 3.3
一个因数=积÷另一个因数
探究二
x=3.3是不是6x=19.8的解呢?
我们可以把x=3.3代入原方程6x=19.8 ,看看能不能使方程左右两边相等
检验:
把X=3.3代入原方程。
方程左边=6X=6 × 3.3=19.8,
方程右边=19.8。
因为左边=右边,
所以X=3.3是原方程的解。
解方程:x +3 = 9
探究二
x=6 是不是x+3=9的解呢?
检验:
把X=6代入原方程。
方程左边=x+3=6+3=9,
方程右边=9。
因为左边=右边,
所以X=6是原方程的解。
x +3 = 9
解: x = 9–3
x = 6
一个加数=和–另一个加数
解方程:6x=19.8
6x = 19.8
解: x = 19.8÷6
x = 3.3
探究二
x=3.3是不是6x=19.8的解呢?
检验:
把X=3.3代入原方程。
方程左边=6X=6 × 3.3=19.8,
方程右边=19.8。
因为左边=右边,
所以X=3.3是原方程的解。
解方程的格式要求:
解方程时先写“ 解:” 。
各行的等号要对齐。
想想未知数表示什么数,用到哪个关系式。
验算以“检验”的形式进行,有固定的格式。
没有书面检验要求的要进行口头检验,养成检验的好习惯。
X=13.8
检验:
把__________代入原方程。
方程左边=_____=______=_____,
方程右边=______。
因为_________,
所以________是原方程的解。
检验:
把X=46.8代入原方程。
方程左边=X÷6=46.8÷6=7.8,
方程右边=7.8。
因为左边=右边,
所以x=46.8是原方程的解。
X÷6=7.8
X=
X=
X=7.8 × 6
X=46.8
解:
7.8
6
13.8
+
X=13.8
X-6
13.8-6
7.8
7.8
左边=右边
解:
X – 6=7.8
比较两个方程的相同点和不同点?
巩固练习1
被减数=减数+差
被除数=商×除数
巩固练习2
练习册P59
X=7
检验:
把__________代入原方程。
方程左边=_____=______=_____,
方程右边=______。
因为_________,
所以________是原方程的解。
17.5÷x=2.5
X=
X=
X=17.5 ÷ 2.5
X=7
解:
15
8
7
-
X=7
15-x
15-7
8
8
左边=右边
解:
15 – x=8
巩固练习2
减数=被减数-差
除数=被除数÷商
练习册P59 B级
巩固练习3
小法官:判断
巩固练习4
回顾小结:
解方程的格式要求:
解方程时先写“ 解:” 。
各行的等号要对齐。
想想未知数表示什么数,用到哪个关系式。
验算以“检验”的形式进行,有固定的格式。
没有书面检验要求的要进行口头检验,养成检验的好习惯。
同课章节目录
