全等三角形学案
图片预览




文档简介
课题: 命题与定理 课型: 新授 课时: 1 复核:
八年级: 班 姓名: 授课教师: 授课时间:
【学习目标】了解命题、定义的含义;对命题的概念有正确的理解。会区分命题的条件和结论。知道判断一个命题是假命题的方法。
【学习重点】找出命题的条件(题设)和结论。
【学习难点】命题概念的理解
教法指导
学习流程(教学流程)
学法指导
预见性问题:
命题的组成学生不熟悉。
对于简写的命题,学生改写正确率不高。
题设应补充完整。结论也应补充完整。
一、知识链接:
试判断下列句子是否正确。 1、如果两个角是对顶角,那么这两个角相等; 2、两直线平行,同位角相等; 3、同旁内角相等,两直线平行; 4、平行四边形的对角线相等; 5、直角都相等。
二、自主学习:
根据已有的知识可以判断出句子_______是正确的,句子______错误的。
★★像这样可以判断出它是____________的句子叫做______,正确的命题称为_______,错误的命题称为_____.
★★许多命题是由_______________两部分组成的。题设是_________;结论是由______________,这样的命题常可写成“_____________”的形式。用“如果”开始的部分就是_______,而用“那么”开始的部分就是______。例如,在命题1中,“___________”是题设,“__________”就是结论。 ????? 有的命题的题设与结论不十分明显,可以将它写成“如果.........,那么...........”的形式,就可以分清它的题设和结论了。例如,命题5可写成“如果两个角是____,那么这两个角______。” 1、把命题“三个角都相等的三角形是等边三角形”改写成“如果___________________.,那么________________.”的形式,并分别指出命题的题设和结论。
2、把下列命题写成“如果.....,那么......”的形式,并说出它们的条件和结论,再判断它是真命题,还是假命题。 (1)对顶角相等; (2)如果a> b,b> c, 那么a=c; (3)菱形的四条边都相等; ★★假命题的证明
要判断一个命题是真命题,可以用逻辑推理的方法加以论证;而要判断一个命题是假命题,只要_______________,即只要举出一个符合该命题题设而不符合该命题结论的例子就可以了,在数学中,这种方法称为“_________”。 ????? 例如,要证明命题“一个锐角与一个钝角的和等于一个平角”是假命题,只要举出一个反例:____________
三、小组合作,展示提升
1、课本P65练习第1、2题。
2、课本习题19.1第1题、第2题。
任务分配:
注意:命题的组成由几部分组成。
【反思总结】
本节课学习了哪些知识:
本节课没有弄懂的有哪些:
课题: 公理、定理 课型: 新授 课时: 1 复核:
八年级: 班 姓名: 授课教师: 授课时间:
【学习目标】了解命题、公理 、定理的含义;理解证明的必要性
【学习重点】知道什么是公理,什么是定理。
【学习难点】理解证明的必要性。
教法指导
学习流程(教学流程)
学法指导
预见性问题。
1、对于公理与定理还不能正确的区分。
2、证明文字性命题的证明,学生还不熟悉。
一、知识链接:
1、要证明一个命题是假命题,应怎么办?
二、自主学习:
这节课,我们将探究怎?? 样证明一个命题是真命题。
★公理
数学中有些命题的_______是人们在长期实践中总结出来的,并把它们作为判断__________,这样的真命题叫做_________。 我们已经知道下列命题是真命题: 一条直线截两条平行直线所得的同位角相等; 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行; 全等三角形的对应边、对应角相等。
我们将这些真命题均作为_________。
★★定理
通过举反例来说明下面两题中归纳出的结论是错误的。
1、请大家看下面的例子: 当n=1时,(n2-5n+5)2=1; 当n=2时,(n2-5n+5)2=1; 当n=3时,(n2-5n+5)2=1。 我们能不能就此下这样的结论:对于任意的正整数(n2-5n+5)2的值都是1呢?
2、如果a=b,那么a2=b2.由此我们猜想:当a> b时,a2> b2。这个命题是真命题吗?
★★数学中有些命题可以从公理出发用逻辑推理的方法证明它们是正确的,并且可以进一步作为推断其他命题真假的依据,这样的真命题叫做_________。
3、例如,有了“三角形的内角和等于180°”这条定理后,我们还可以证明刻画直角三角形的两个锐角之间的数量关系的命题:直角三角形的两个锐角互余。 请证明:直角三角形的两个锐角互余
三、小组合作,展示提升
1、课本P66练习第1、2题
2、课本习题19.1第3题
任务分配:
n=5时结论不成立。
没有几何图形是应注意先画图。写出已知、求证。
【反思总结】
本节课学习了哪些知识:
本节课没有弄懂的有哪些:
课题: 全等三角形的识别(1) 课型: 新授 课时: 1 复核:
八年级: 班 姓名: 授课教师: 授课时间:
【学习目标】1、经历探索三角形全等条件的过程,体会如何探索研究问题。培养学生合作的精神,让学生体验分类的思想;2、懂得如何提出问题,分类讨论,并为以后研究提出问题。
【学习重点】培养学生探索问题能力;
【学习难点】掌握探索问题的方法。
教法指导
学习流程(教学流程)
学法指导
预见性问题
1、全等三角形 的识别学生已经忘记。
2、全等三角形的几何语言应注意些什么?
3、利用全等三角形的性质解决问题。
4、引导学生采用分类讨论思想进行探究。
一、知识链接:
三角形全等:1、若两个三角形的______条边和______个角分别对应相等,则这两个三角形______.
2、如图,△ABC≌△CDA,,,求出△ADC各内角的度数。
二、自主学习:
1、两个三角形全等需要几个条件?
2、能否减少一些条件,至少要有几个条件(元素)本别对应相等,两个三角形才会全等呢?(可能是一个条件、两个条件、三个条件……)
★一个条件(元素)对应相等,这两个三角形一定全等吗?
做一做:(1)只给一个条件:一条边,大家画出三角形,小组交流画的三角形全等吗?一个角,大家画出三角形,小组交流画的三角形全等吗?
结论:________________________________________
★两个条件(元素)对应相等,这两个三角形一定全等吗?
做一做:分别按照下面条件,用刻度尺或量角器画三角形,并和周围的同学比较一下,所画的图形是否全等。
①三角形的一个内角为60°,一条边为3 cm;
② 三角形的两个内角分别为30°和70°;
③ 三角形的两条边分别为3 cm和5 cm
结论:________________________________________
★三个条件(元素)对应相等,这两个三角形一定全等吗?
如果给出三个条件画三角形,你能说出有哪几种可能的情况?__________________________________.
对于按以上每一种可能画得三角形是否全等,下一节课一起分别逐个探讨研究。
三、小组合作,展示提升
1、如图,点O是平行四边形ABCD的对角线的交点,△AOB绕O旋转180o,可以与△___________重合,这说明△AOB≌△___________.这两个三角形的对应边是AO与__________,OB与__________,BA与__________;对应角是∠AOB与________,∠OBA与_________,∠BAO与___________。
2、如图,△ABC是等腰三角形,AD是底边上的高,△ABD和△ACD全等吗?试根据等腰三角形的有关知识说明理由
四、练习
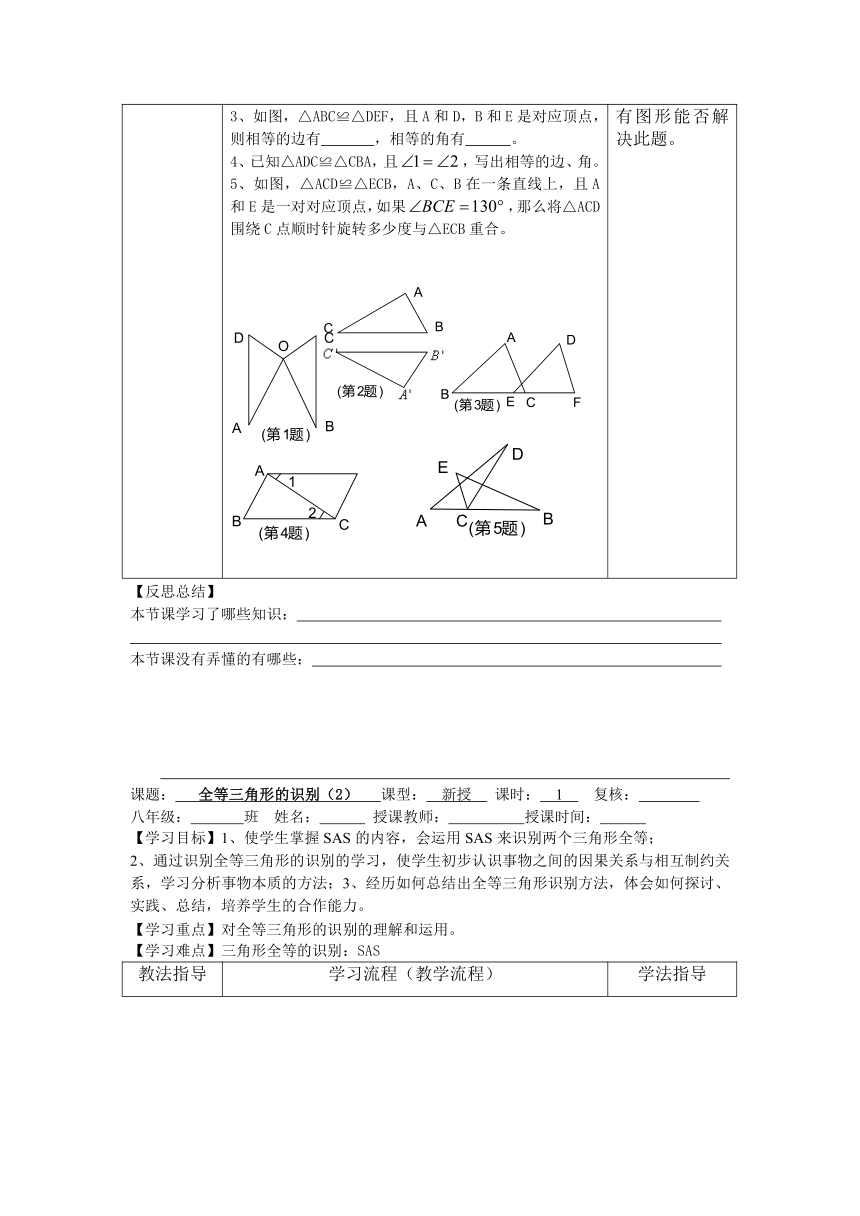
1、如图,△AOD≌△BOC,写出其中相等的角
2、如图,△ABC≌△,,,
3、如图,△ABC≌△DEF,且A和D,B和E是对应顶点,则相等的边有 ,相等的角有 。
4、已知△ADC≌△CBA,且,写出相等的边、角。
5、如图,△ACD≌△ECB,A、C、B在一条直线上,且A和E是一对对应顶点,如果,那么将△ACD围绕C点顺时针旋转多少度与△ECB重合。
三角形全等的书写有什么要求?
任务分配:
全等多边形的性质
1题中如果没有图形能否解决此题。
【反思总结】
本节课学习了哪些知识:
本节课没有弄懂的有哪些:
课题: 全等三角形的识别(2) 课型: 新授 课时: 1 复核:
八年级: 班 姓名: 授课教师: 授课时间:
【学习目标】1、使学生掌握SAS的内容,会运用SAS来识别两个三角形全等;
2、通过识别全等三角形的识别的学习,使学生初步认识事物之间的因果关系与相互制约关系,学习分析事物本质的方法;3、经历如何总结出全等三角形识别方法,体会如何探讨、实践、总结,培养学生的合作能力。
【学习重点】对全等三角形的识别的理解和运用。
【学习难点】三角形全等的识别:SAS
教法指导
学习流程(教学流程)
学法指导
预见性问题
1、学生使用尺规画三角形,有一定难度,需要老师指导。
2、两边一角判定全等,当角不是夹角时,不全等,学生易错。
3、判断全等三角形的几何语言书写需进一步规范。
一、知识链接:
两个三角形有3个条件(元素)对应相等,有哪几种可能的情况?__________________________________.
本节起将分别逐个探讨研究。
二、自主学习:
★1、三个角对应相等、三条边对应相等的两个三角形一定全等吗?
(1)画一个三角形,使三边长尾3、4、5厘米。
(2)画一个三角形,使三个角的度数为30度、60度、90度。
小组交流所画三角形是否全等。
结论:__________________________________________
★问题1:如果已知一个三角形的两边及一角,那么有几种可能的情况呢?____________________________.每一种情况下得到的三角形都全等吗?
★如果两个三角形有两边及其夹角分别对应相等,这两个三角形全等吗?
做一做:
三角形两条边分别为和,它们的夹角为,画出这个三角形,小组内交流所画的一定全等吗?
★结论:_________________________________________
简写成“边角边”或简记为(S.A.S.)
几何语言:_____________
_______________
“两边及一角”条件中的角是其中一边的对角,这两个三角形一定全等吗?
做一做:
三角形的两条边分别为和,长度为的边所对的角为。画出这个三角形,小组内交流所画的一定全等吗?
★结论:_________________________________________
三、小组合作,展示提升
1、P71 练习1、2
2、P79习题 2
3、如图,△ABC中,AB=AC,AD平分∠BAC,试说明△ABD≌△ACD.
任务分配:
自己动手画一画
注意:三角形全等的几何语言
【反思总结】
本节课学习了哪些知识:
本节课没有弄懂的有哪些:
课题: 全等三角形的识别(3) 课型: 新授 课时: 1 复核:
八年级: 班 姓名: 授课教师: 授课时间:
【学习目标】1、使学生理解ASA的内容,能运用ASA全等识别法来识别三角形全等进而说明线段或角相等;2、通过画图、实验、发现、应用的过程教学,树立学生知识源于实践用于实践的观念。使学生体会探索发现问题的过程。经历自己探索出AAS的三角形全等识别及其应用。
【学习重点】利用三角形全等的识别法,间接说明角相等或线段相等。
【学习难点】三角形全等的识别法ASA和AAS及应用
教法指导
学习流程(教学流程)
学法指导
预见性问题
1、两角一边的判定与两边一角的判定的异同。
2、全等三角形判定的几何语言书写规范。
一、知识链接:
1、什么叫做全等三角形,如何识别两个三角形全等?
2、叙述SSS、SAS的内容。
3、已知:如图,AB=DE,AC=DF,请问再加上什么条件下,△ABC≌△DEF,并说明理由。
二、自主学习:
★已知一个三角形的两角及一边,那么有几种可能的情况呢?_____________________________________
(1) 两个角及两角的夹边对应相等,这两个三角形一定全等吗?
做一做:画一个三角形,使两个角为30度和50度,其夹边为3厘米。小组交流所画三角形全等吗?
★结论:____________________________________
_________________简记为“角边角”或简记为(A.S.A.)
几何语言:______________
___________________
两个角及其中一角的对边对应相等,这两个三角形一定全等吗?
做一做:画一个三角形,使两个角为30度和50度,其30度的角所对的边为3厘米。小组交流所画三角形全等吗?
★结论:____________________________________
_________________简写成:“角角边”或简记为(A. A. S.)。
几何语言:______________
___________________
问题3:你能说说ASA与AAS这两种全等识别法间的关系吗?
三、小组合作,展示提升
1、P74练习 1、2
2、P79习题3、4、5
3、如图,,,试说明△ABC≌△DCB
任务分配:
注意:两边一角,角只能为夹角。
注意与边角边的区别。
在教材上完成,要进行展示。
【反思总结】
本节课学习了哪些知识:
本节课没有弄懂的有哪些:
课题: 全等三角形的识别(4) 课型: 新授 课时: 1 复核:
八年级: 班 姓名: 授课教师: 授课时间:
【学习目标】1、经历探索直角三角形全等条件HL的过程,掌握直角三角形全等的条件,并能运用其解决一些实际问题;2、学习事物的特殊、一般关系、发展逻辑思维能力。
【学习重点】让学生掌握直角三角形全等的“HL”识别法
【学习难点】理解直角三角形为内角在构造三角形时特殊性,并能灵活地运用各种全等识别法识别两个直角三角形全等是否全等。
教法指导
学习流程(教学流程)
学法指导
预见性问题
1、斜边直角边表面上看只有两个条件,其实是三个条件,缺一不可。
2、此判定的使用范围仅限于直角三角形,其他三角形不能用这个判定。
3、注意几何语言的规范性。
注意作图步骤。
一、知识链接:
如图,△ABC和△都是直角三角形,请你用所学的知识,须加上什么条件直角△ABC和△全等。并说明理由。
[,,(SAS);
,(ASA);
,,(SSS)
,(AAS)]
二、自主学习:
引入:舞台背景的形状是两个直角三角形。工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆计划遮住无法测量。
1、你能帮他想个办法吗?
2、如果他只带了一个卷尺,能完成这个任务吗?
我们已经知道,如果有“边边角”分别对应相等,那么也不能保证这两个三角形全等.
那么在两个直角三角形中,当斜边和一条直角边分别对应相等时,也具有“边边角”对应相等的条件,这时这两个直角三角形能否全等呢?
做一做:已知两条线段(这两条线段长不相等),以长的线段为斜边、短的线段为一条直角边,画一个直角三角形.
把你画的直角三角形与其他同学画的直角三角形进行比较,所有的直角三角形都全等吗?__________
★结论:_________________________________________
简记为H.L.(或斜边直角边)
几何语言:____________
______________ ____________
三、小组合作,展示提升
1/如图19.2.18,已知AC=BD, ∠C=∠D=90°,求证Rt△ABC≌Rt△BAD.
证明∵ ∠C=∠D=90°,
∴ _______________.
在Rt△ABC与Rt△BAD中,
∵ AB=BA,
AC=BD,
∴ _________(_____).
2、P79 练习1、2
3、P79习题 6
注意每个判定的条件。
步骤:
1. 画一线段AB,使它等于4cm;
2. 画∠MAB=90°;
3. 以点B为圆心,以5cm长为半径画圆弧,交射线AM于点C;
4. 连结BC.
△ABC即为所求.
注意几何语言的规范性。
【反思总结】
本节课学习了哪些知识:
本节课没有弄懂的有哪些:
课题: 全等三角形的识别(复习) 课型: 新授 课时: 1 复核:
八年级: 班 姓名: 授课教师: 授课时间:
【学习目标】1、总结一般三角形全等的识别条件,能自觉运用各种全等识别法进行说理;2、通过一般三角形全等识别条件的归纳,认识事物间存在着的因果关系和制约的关系
【学习重点】识别三角的哪些元素能用来确定三角形的形状与大小,因而可用来识别三角形全等。
【学习难点】灵活应用各种识别法识别全等三角形。
教法指导
学习流程(教学流程)
学法指导
预见性问题
1、学生对全等三角形的判定方法不熟悉。
2、不能正确区分几种全等三角形判定方法。
3、倒推法学生比较陌生,需要强化训练。
一、知识链接:
1、识别两个三角形全等的条件有哪些?
(有______,_______,_______,_______,_________)
2、一个三角形共有三条边与三个角,你是否想到这样一问题了:除了上述四种识别法,还有其他的三角形全等识别法吗?比如说“SSA”、“AAA”能成为判定两个三角形全等的条件吗?
二、自主学习:
1、完成下列表格。
两个三角
形中对应
相等的元素
两个三角
形是否全
等
依据的
识别法
反例
SSS
SSS
SAS
SAS
SSA
可举
反例
ASA
ASA
AAS
AAS
AAA
可举
反例
2、如图,,,点F是CD的中点,吗?试说明理由。
分析要点:(1)分析题目结论假定,可转化为_______________,需证它们所在的两个三角形全等;
(2)观察图形,、中,并不在三角形中,为此________;(怎样添加辅助线)
(3)在△ACF与△ADF中,已知AF是公共边,CF=FD,尚缺一条件,它只能是_________相等;
(4)为证AC与AD相等。只需要证_________
(5)要证△ACB与△ADE,由已知条件可由SAS证它们全等;
(6)书写范例。
解:
2、如图,在△ABC中,,,试说明△AED是等腰三角形。
3、如图,AB∥CD,AD∥BC,与,与相等吗?说明理由。
三、小组合作,展示提升
(一)、填空题:
1、有一边对应相等的两个 三角形全等;
2、有一边和 对应相等的两个三角形全等;
3、有两边和 一角对应相等的两个三角形全等;
4、如图,AB∥CD,AD∥BC,AC、BD相交于点O。
(1)由AD∥BC,可得 = ,由AB∥CD,可得 = ,又由 ,于是△ABD≌△CDB;
(2)由 ,可得AD=CB,由 ,可得△AOD≌△COB;
(3)图中全等三角形共有 对。
(二)、选择题:
1、若△ABC≌△BAD,A和B、C和D是对应顶点,如果,,,则BC的长是( )
A、 B、 C、 D、无法确定
2、下列各说法中,正确的是( )
A、有两边和一角对应相等的两个三角形全等;
B、有两个角对应相等且周长相等的两个三角形全等;
C、两个锐角对应相等的两个直角三角形全等;
D、有两组边相等且周长相等的两个三角形全等。
(三)、解答题:
1、如图,,,AC、BD交于点,图中共有几对长度相等的线段,请说明理由?
2、如图,,,
(1)等于多少度?
(2)图中有哪几组平行线?
(3)与的和是定值吗?
任务分配
此题从问题出发进行分析,要学会倒推法哦!
可尝试用倒推法进行分析。
作辅助线,构成三角形,利用全等三角形来进行解决。
【反思总结】
本节课学习了哪些知识:
本节课没有弄懂的有哪些:
八年级: 班 姓名: 授课教师: 授课时间:
【学习目标】了解命题、定义的含义;对命题的概念有正确的理解。会区分命题的条件和结论。知道判断一个命题是假命题的方法。
【学习重点】找出命题的条件(题设)和结论。
【学习难点】命题概念的理解
教法指导
学习流程(教学流程)
学法指导
预见性问题:
命题的组成学生不熟悉。
对于简写的命题,学生改写正确率不高。
题设应补充完整。结论也应补充完整。
一、知识链接:
试判断下列句子是否正确。 1、如果两个角是对顶角,那么这两个角相等; 2、两直线平行,同位角相等; 3、同旁内角相等,两直线平行; 4、平行四边形的对角线相等; 5、直角都相等。
二、自主学习:
根据已有的知识可以判断出句子_______是正确的,句子______错误的。
★★像这样可以判断出它是____________的句子叫做______,正确的命题称为_______,错误的命题称为_____.
★★许多命题是由_______________两部分组成的。题设是_________;结论是由______________,这样的命题常可写成“_____________”的形式。用“如果”开始的部分就是_______,而用“那么”开始的部分就是______。例如,在命题1中,“___________”是题设,“__________”就是结论。 ????? 有的命题的题设与结论不十分明显,可以将它写成“如果.........,那么...........”的形式,就可以分清它的题设和结论了。例如,命题5可写成“如果两个角是____,那么这两个角______。” 1、把命题“三个角都相等的三角形是等边三角形”改写成“如果___________________.,那么________________.”的形式,并分别指出命题的题设和结论。
2、把下列命题写成“如果.....,那么......”的形式,并说出它们的条件和结论,再判断它是真命题,还是假命题。 (1)对顶角相等; (2)如果a> b,b> c, 那么a=c; (3)菱形的四条边都相等; ★★假命题的证明
要判断一个命题是真命题,可以用逻辑推理的方法加以论证;而要判断一个命题是假命题,只要_______________,即只要举出一个符合该命题题设而不符合该命题结论的例子就可以了,在数学中,这种方法称为“_________”。 ????? 例如,要证明命题“一个锐角与一个钝角的和等于一个平角”是假命题,只要举出一个反例:____________
三、小组合作,展示提升
1、课本P65练习第1、2题。
2、课本习题19.1第1题、第2题。
任务分配:
注意:命题的组成由几部分组成。
【反思总结】
本节课学习了哪些知识:
本节课没有弄懂的有哪些:
课题: 公理、定理 课型: 新授 课时: 1 复核:
八年级: 班 姓名: 授课教师: 授课时间:
【学习目标】了解命题、公理 、定理的含义;理解证明的必要性
【学习重点】知道什么是公理,什么是定理。
【学习难点】理解证明的必要性。
教法指导
学习流程(教学流程)
学法指导
预见性问题。
1、对于公理与定理还不能正确的区分。
2、证明文字性命题的证明,学生还不熟悉。
一、知识链接:
1、要证明一个命题是假命题,应怎么办?
二、自主学习:
这节课,我们将探究怎?? 样证明一个命题是真命题。
★公理
数学中有些命题的_______是人们在长期实践中总结出来的,并把它们作为判断__________,这样的真命题叫做_________。 我们已经知道下列命题是真命题: 一条直线截两条平行直线所得的同位角相等; 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行; 全等三角形的对应边、对应角相等。
我们将这些真命题均作为_________。
★★定理
通过举反例来说明下面两题中归纳出的结论是错误的。
1、请大家看下面的例子: 当n=1时,(n2-5n+5)2=1; 当n=2时,(n2-5n+5)2=1; 当n=3时,(n2-5n+5)2=1。 我们能不能就此下这样的结论:对于任意的正整数(n2-5n+5)2的值都是1呢?
2、如果a=b,那么a2=b2.由此我们猜想:当a> b时,a2> b2。这个命题是真命题吗?
★★数学中有些命题可以从公理出发用逻辑推理的方法证明它们是正确的,并且可以进一步作为推断其他命题真假的依据,这样的真命题叫做_________。
3、例如,有了“三角形的内角和等于180°”这条定理后,我们还可以证明刻画直角三角形的两个锐角之间的数量关系的命题:直角三角形的两个锐角互余。 请证明:直角三角形的两个锐角互余
三、小组合作,展示提升
1、课本P66练习第1、2题
2、课本习题19.1第3题
任务分配:
n=5时结论不成立。
没有几何图形是应注意先画图。写出已知、求证。
【反思总结】
本节课学习了哪些知识:
本节课没有弄懂的有哪些:
课题: 全等三角形的识别(1) 课型: 新授 课时: 1 复核:
八年级: 班 姓名: 授课教师: 授课时间:
【学习目标】1、经历探索三角形全等条件的过程,体会如何探索研究问题。培养学生合作的精神,让学生体验分类的思想;2、懂得如何提出问题,分类讨论,并为以后研究提出问题。
【学习重点】培养学生探索问题能力;
【学习难点】掌握探索问题的方法。
教法指导
学习流程(教学流程)
学法指导
预见性问题
1、全等三角形 的识别学生已经忘记。
2、全等三角形的几何语言应注意些什么?
3、利用全等三角形的性质解决问题。
4、引导学生采用分类讨论思想进行探究。
一、知识链接:
三角形全等:1、若两个三角形的______条边和______个角分别对应相等,则这两个三角形______.
2、如图,△ABC≌△CDA,,,求出△ADC各内角的度数。
二、自主学习:
1、两个三角形全等需要几个条件?
2、能否减少一些条件,至少要有几个条件(元素)本别对应相等,两个三角形才会全等呢?(可能是一个条件、两个条件、三个条件……)
★一个条件(元素)对应相等,这两个三角形一定全等吗?
做一做:(1)只给一个条件:一条边,大家画出三角形,小组交流画的三角形全等吗?一个角,大家画出三角形,小组交流画的三角形全等吗?
结论:________________________________________
★两个条件(元素)对应相等,这两个三角形一定全等吗?
做一做:分别按照下面条件,用刻度尺或量角器画三角形,并和周围的同学比较一下,所画的图形是否全等。
①三角形的一个内角为60°,一条边为3 cm;
② 三角形的两个内角分别为30°和70°;
③ 三角形的两条边分别为3 cm和5 cm
结论:________________________________________
★三个条件(元素)对应相等,这两个三角形一定全等吗?
如果给出三个条件画三角形,你能说出有哪几种可能的情况?__________________________________.
对于按以上每一种可能画得三角形是否全等,下一节课一起分别逐个探讨研究。
三、小组合作,展示提升
1、如图,点O是平行四边形ABCD的对角线的交点,△AOB绕O旋转180o,可以与△___________重合,这说明△AOB≌△___________.这两个三角形的对应边是AO与__________,OB与__________,BA与__________;对应角是∠AOB与________,∠OBA与_________,∠BAO与___________。
2、如图,△ABC是等腰三角形,AD是底边上的高,△ABD和△ACD全等吗?试根据等腰三角形的有关知识说明理由
四、练习
1、如图,△AOD≌△BOC,写出其中相等的角
2、如图,△ABC≌△,,,
3、如图,△ABC≌△DEF,且A和D,B和E是对应顶点,则相等的边有 ,相等的角有 。
4、已知△ADC≌△CBA,且,写出相等的边、角。
5、如图,△ACD≌△ECB,A、C、B在一条直线上,且A和E是一对对应顶点,如果,那么将△ACD围绕C点顺时针旋转多少度与△ECB重合。
三角形全等的书写有什么要求?
任务分配:
全等多边形的性质
1题中如果没有图形能否解决此题。
【反思总结】
本节课学习了哪些知识:
本节课没有弄懂的有哪些:
课题: 全等三角形的识别(2) 课型: 新授 课时: 1 复核:
八年级: 班 姓名: 授课教师: 授课时间:
【学习目标】1、使学生掌握SAS的内容,会运用SAS来识别两个三角形全等;
2、通过识别全等三角形的识别的学习,使学生初步认识事物之间的因果关系与相互制约关系,学习分析事物本质的方法;3、经历如何总结出全等三角形识别方法,体会如何探讨、实践、总结,培养学生的合作能力。
【学习重点】对全等三角形的识别的理解和运用。
【学习难点】三角形全等的识别:SAS
教法指导
学习流程(教学流程)
学法指导
预见性问题
1、学生使用尺规画三角形,有一定难度,需要老师指导。
2、两边一角判定全等,当角不是夹角时,不全等,学生易错。
3、判断全等三角形的几何语言书写需进一步规范。
一、知识链接:
两个三角形有3个条件(元素)对应相等,有哪几种可能的情况?__________________________________.
本节起将分别逐个探讨研究。
二、自主学习:
★1、三个角对应相等、三条边对应相等的两个三角形一定全等吗?
(1)画一个三角形,使三边长尾3、4、5厘米。
(2)画一个三角形,使三个角的度数为30度、60度、90度。
小组交流所画三角形是否全等。
结论:__________________________________________
★问题1:如果已知一个三角形的两边及一角,那么有几种可能的情况呢?____________________________.每一种情况下得到的三角形都全等吗?
★如果两个三角形有两边及其夹角分别对应相等,这两个三角形全等吗?
做一做:
三角形两条边分别为和,它们的夹角为,画出这个三角形,小组内交流所画的一定全等吗?
★结论:_________________________________________
简写成“边角边”或简记为(S.A.S.)
几何语言:_____________
_______________
“两边及一角”条件中的角是其中一边的对角,这两个三角形一定全等吗?
做一做:
三角形的两条边分别为和,长度为的边所对的角为。画出这个三角形,小组内交流所画的一定全等吗?
★结论:_________________________________________
三、小组合作,展示提升
1、P71 练习1、2
2、P79习题 2
3、如图,△ABC中,AB=AC,AD平分∠BAC,试说明△ABD≌△ACD.
任务分配:
自己动手画一画
注意:三角形全等的几何语言
【反思总结】
本节课学习了哪些知识:
本节课没有弄懂的有哪些:
课题: 全等三角形的识别(3) 课型: 新授 课时: 1 复核:
八年级: 班 姓名: 授课教师: 授课时间:
【学习目标】1、使学生理解ASA的内容,能运用ASA全等识别法来识别三角形全等进而说明线段或角相等;2、通过画图、实验、发现、应用的过程教学,树立学生知识源于实践用于实践的观念。使学生体会探索发现问题的过程。经历自己探索出AAS的三角形全等识别及其应用。
【学习重点】利用三角形全等的识别法,间接说明角相等或线段相等。
【学习难点】三角形全等的识别法ASA和AAS及应用
教法指导
学习流程(教学流程)
学法指导
预见性问题
1、两角一边的判定与两边一角的判定的异同。
2、全等三角形判定的几何语言书写规范。
一、知识链接:
1、什么叫做全等三角形,如何识别两个三角形全等?
2、叙述SSS、SAS的内容。
3、已知:如图,AB=DE,AC=DF,请问再加上什么条件下,△ABC≌△DEF,并说明理由。
二、自主学习:
★已知一个三角形的两角及一边,那么有几种可能的情况呢?_____________________________________
(1) 两个角及两角的夹边对应相等,这两个三角形一定全等吗?
做一做:画一个三角形,使两个角为30度和50度,其夹边为3厘米。小组交流所画三角形全等吗?
★结论:____________________________________
_________________简记为“角边角”或简记为(A.S.A.)
几何语言:______________
___________________
两个角及其中一角的对边对应相等,这两个三角形一定全等吗?
做一做:画一个三角形,使两个角为30度和50度,其30度的角所对的边为3厘米。小组交流所画三角形全等吗?
★结论:____________________________________
_________________简写成:“角角边”或简记为(A. A. S.)。
几何语言:______________
___________________
问题3:你能说说ASA与AAS这两种全等识别法间的关系吗?
三、小组合作,展示提升
1、P74练习 1、2
2、P79习题3、4、5
3、如图,,,试说明△ABC≌△DCB
任务分配:
注意:两边一角,角只能为夹角。
注意与边角边的区别。
在教材上完成,要进行展示。
【反思总结】
本节课学习了哪些知识:
本节课没有弄懂的有哪些:
课题: 全等三角形的识别(4) 课型: 新授 课时: 1 复核:
八年级: 班 姓名: 授课教师: 授课时间:
【学习目标】1、经历探索直角三角形全等条件HL的过程,掌握直角三角形全等的条件,并能运用其解决一些实际问题;2、学习事物的特殊、一般关系、发展逻辑思维能力。
【学习重点】让学生掌握直角三角形全等的“HL”识别法
【学习难点】理解直角三角形为内角在构造三角形时特殊性,并能灵活地运用各种全等识别法识别两个直角三角形全等是否全等。
教法指导
学习流程(教学流程)
学法指导
预见性问题
1、斜边直角边表面上看只有两个条件,其实是三个条件,缺一不可。
2、此判定的使用范围仅限于直角三角形,其他三角形不能用这个判定。
3、注意几何语言的规范性。
注意作图步骤。
一、知识链接:
如图,△ABC和△都是直角三角形,请你用所学的知识,须加上什么条件直角△ABC和△全等。并说明理由。
[,,(SAS);
,(ASA);
,,(SSS)
,(AAS)]
二、自主学习:
引入:舞台背景的形状是两个直角三角形。工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆计划遮住无法测量。
1、你能帮他想个办法吗?
2、如果他只带了一个卷尺,能完成这个任务吗?
我们已经知道,如果有“边边角”分别对应相等,那么也不能保证这两个三角形全等.
那么在两个直角三角形中,当斜边和一条直角边分别对应相等时,也具有“边边角”对应相等的条件,这时这两个直角三角形能否全等呢?
做一做:已知两条线段(这两条线段长不相等),以长的线段为斜边、短的线段为一条直角边,画一个直角三角形.
把你画的直角三角形与其他同学画的直角三角形进行比较,所有的直角三角形都全等吗?__________
★结论:_________________________________________
简记为H.L.(或斜边直角边)
几何语言:____________
______________ ____________
三、小组合作,展示提升
1/如图19.2.18,已知AC=BD, ∠C=∠D=90°,求证Rt△ABC≌Rt△BAD.
证明∵ ∠C=∠D=90°,
∴ _______________.
在Rt△ABC与Rt△BAD中,
∵ AB=BA,
AC=BD,
∴ _________(_____).
2、P79 练习1、2
3、P79习题 6
注意每个判定的条件。
步骤:
1. 画一线段AB,使它等于4cm;
2. 画∠MAB=90°;
3. 以点B为圆心,以5cm长为半径画圆弧,交射线AM于点C;
4. 连结BC.
△ABC即为所求.
注意几何语言的规范性。
【反思总结】
本节课学习了哪些知识:
本节课没有弄懂的有哪些:
课题: 全等三角形的识别(复习) 课型: 新授 课时: 1 复核:
八年级: 班 姓名: 授课教师: 授课时间:
【学习目标】1、总结一般三角形全等的识别条件,能自觉运用各种全等识别法进行说理;2、通过一般三角形全等识别条件的归纳,认识事物间存在着的因果关系和制约的关系
【学习重点】识别三角的哪些元素能用来确定三角形的形状与大小,因而可用来识别三角形全等。
【学习难点】灵活应用各种识别法识别全等三角形。
教法指导
学习流程(教学流程)
学法指导
预见性问题
1、学生对全等三角形的判定方法不熟悉。
2、不能正确区分几种全等三角形判定方法。
3、倒推法学生比较陌生,需要强化训练。
一、知识链接:
1、识别两个三角形全等的条件有哪些?
(有______,_______,_______,_______,_________)
2、一个三角形共有三条边与三个角,你是否想到这样一问题了:除了上述四种识别法,还有其他的三角形全等识别法吗?比如说“SSA”、“AAA”能成为判定两个三角形全等的条件吗?
二、自主学习:
1、完成下列表格。
两个三角
形中对应
相等的元素
两个三角
形是否全
等
依据的
识别法
反例
SSS
SSS
SAS
SAS
SSA
可举
反例
ASA
ASA
AAS
AAS
AAA
可举
反例
2、如图,,,点F是CD的中点,吗?试说明理由。
分析要点:(1)分析题目结论假定,可转化为_______________,需证它们所在的两个三角形全等;
(2)观察图形,、中,并不在三角形中,为此________;(怎样添加辅助线)
(3)在△ACF与△ADF中,已知AF是公共边,CF=FD,尚缺一条件,它只能是_________相等;
(4)为证AC与AD相等。只需要证_________
(5)要证△ACB与△ADE,由已知条件可由SAS证它们全等;
(6)书写范例。
解:
2、如图,在△ABC中,,,试说明△AED是等腰三角形。
3、如图,AB∥CD,AD∥BC,与,与相等吗?说明理由。
三、小组合作,展示提升
(一)、填空题:
1、有一边对应相等的两个 三角形全等;
2、有一边和 对应相等的两个三角形全等;
3、有两边和 一角对应相等的两个三角形全等;
4、如图,AB∥CD,AD∥BC,AC、BD相交于点O。
(1)由AD∥BC,可得 = ,由AB∥CD,可得 = ,又由 ,于是△ABD≌△CDB;
(2)由 ,可得AD=CB,由 ,可得△AOD≌△COB;
(3)图中全等三角形共有 对。
(二)、选择题:
1、若△ABC≌△BAD,A和B、C和D是对应顶点,如果,,,则BC的长是( )
A、 B、 C、 D、无法确定
2、下列各说法中,正确的是( )
A、有两边和一角对应相等的两个三角形全等;
B、有两个角对应相等且周长相等的两个三角形全等;
C、两个锐角对应相等的两个直角三角形全等;
D、有两组边相等且周长相等的两个三角形全等。
(三)、解答题:
1、如图,,,AC、BD交于点,图中共有几对长度相等的线段,请说明理由?
2、如图,,,
(1)等于多少度?
(2)图中有哪几组平行线?
(3)与的和是定值吗?
任务分配
此题从问题出发进行分析,要学会倒推法哦!
可尝试用倒推法进行分析。
作辅助线,构成三角形,利用全等三角形来进行解决。
【反思总结】
本节课学习了哪些知识:
本节课没有弄懂的有哪些:
