23.2 解直角三角形及其应用(3) 课件(共25张PPT)
文档属性
| 名称 | 23.2 解直角三角形及其应用(3) 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-06 00:00:00 | ||
图片预览



文档简介
(共25张PPT)
沪科版 九年级上册
23.2 解直角三角形及其应用 (3)
仰角、俯角问题(1)
解直角三角形的理论在实际中的应用是学生在熟练掌握了勾股定理,直角三角形中两锐角互余,锐角三角函数,能利用直角三角形中的这些关系解直角三角形的基础上进行教学,主要应让学生学会用直角三角形的有关知识去解决某些简单的实际问题.它既是前面所学知识的运用,也是高中继续解斜三角形的重要预备知识.它的学习还蕴涵着深刻的数学思想方法(数学建模、转化化归),在本节教学中有针对性地对学生进行这方面的能力培养.
课件说明
教学目标: 1.使学生把仰角、俯角问题转化为解直角三角形问题,
从而会把实际问题转化为数学问题来解决,进一步
提高数学建模能力; 2.通过综合运用勾股定理,直角三角形的两个锐角互 余及锐角三角函数解直角三角形,逐步培养学生分 析问题、解决问题的能力.
教学重点: 将仰角、俯角问题中的数量关系,归结为直角三角形
元素之间的关系,从而利用所学知识解决实际题.
课件说明
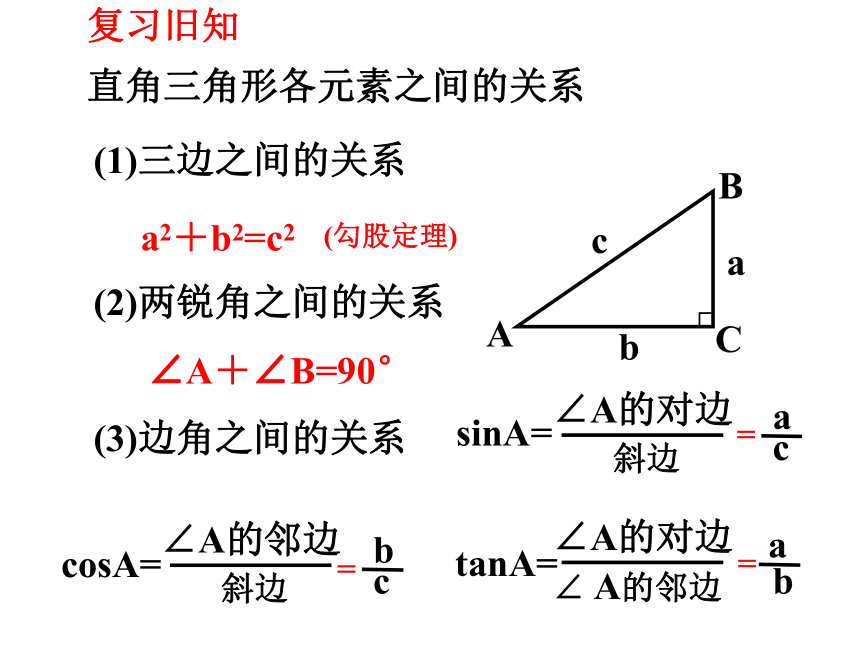
(1)三边之间的关系
A
C
B
c
a
b
直角三角形各元素之间的关系
a2+b2=c2
(勾股定理)
(2)两锐角之间的关系
(3)边角之间的关系
∠A+∠B=90°
斜边
∠A的对边
a
c
sinA=
=
cosA=
斜边
∠A的邻边
=
b
c
tanA=
∠ A的邻边
∠A的对边
=
a
b
复习旧知
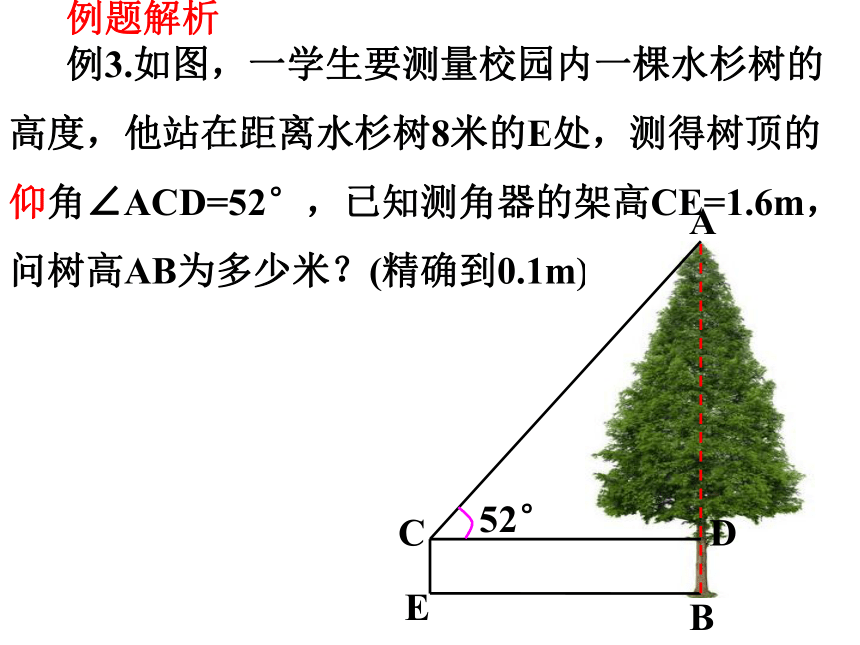
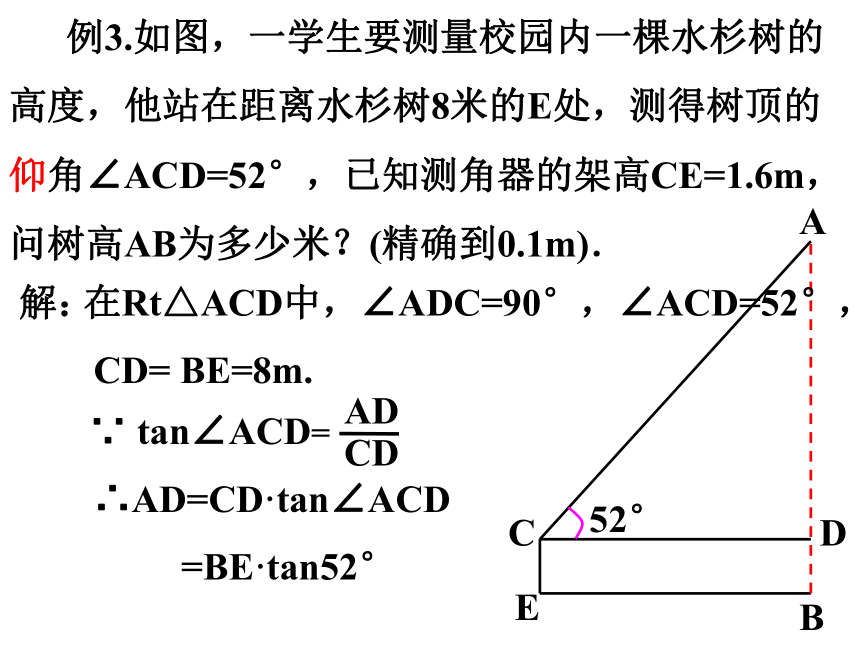
例3.如图,一学生要测量校园内一棵水杉树的高度,他站在距离水杉树8米的E处,测得树顶的仰角∠ACD=52°,已知测角器的架高CE=1.6m,问树高AB为多少米?(精确到0.1m).
A
B
E
C
D
52°
例题解析
铅直线
水平线
视线
视线
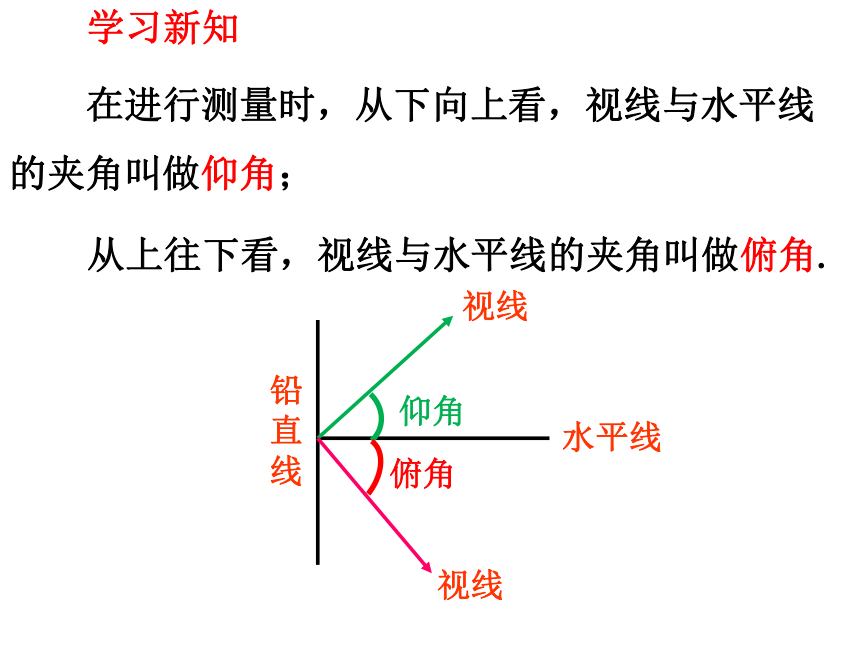
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;
仰角
从上往下看,视线与水平线的夹角叫做俯角.
俯角
学习新知
例3.如图,一学生要测量校园内一棵水杉树的高度,他站在距离水杉树8米的E处,测得树顶的仰角∠ACD=52°,已知测角器的架高CE=1.6m,问树高AB为多少米?(精确到0.1m).
A
B
E
C
D
52°
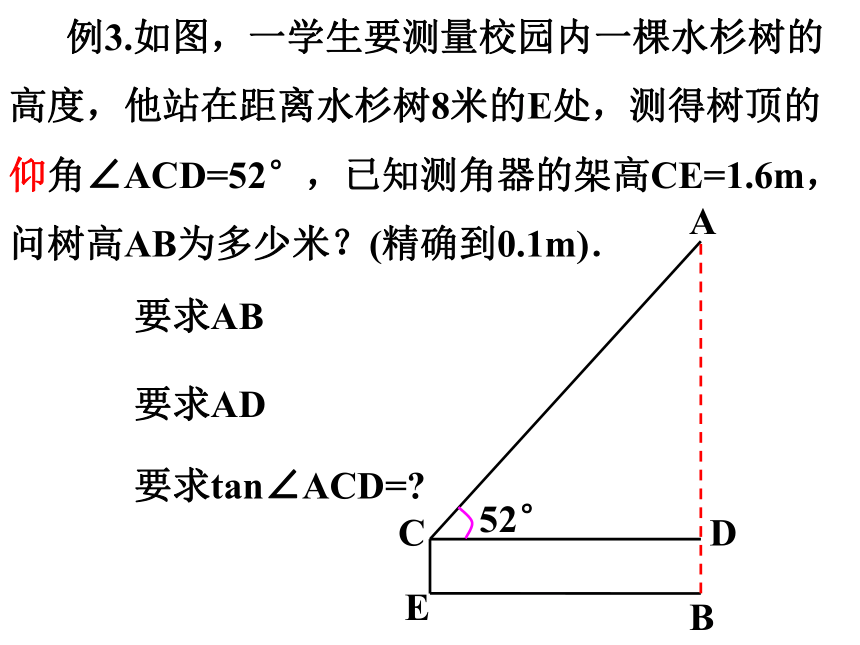
要求AB
要求AD
要求tan∠ACD=
例3.如图,一学生要测量校园内一棵水杉树的高度,他站在距离水杉树8米的E处,测得树顶的仰角∠ACD=52°,已知测角器的架高CE=1.6m,问树高AB为多少米?(精确到0.1m).
A
B
E
C
D
52°
∵ tan∠ACD=
解:
在Rt△ACD中,∠ADC=90°,∠ACD=52°,
AD
CD
CD= BE=8m.
∴AD=CD·tan∠ACD
=BE·tan52°
A
B
E
C
D
52°
∵ tan∠ACD=
解:
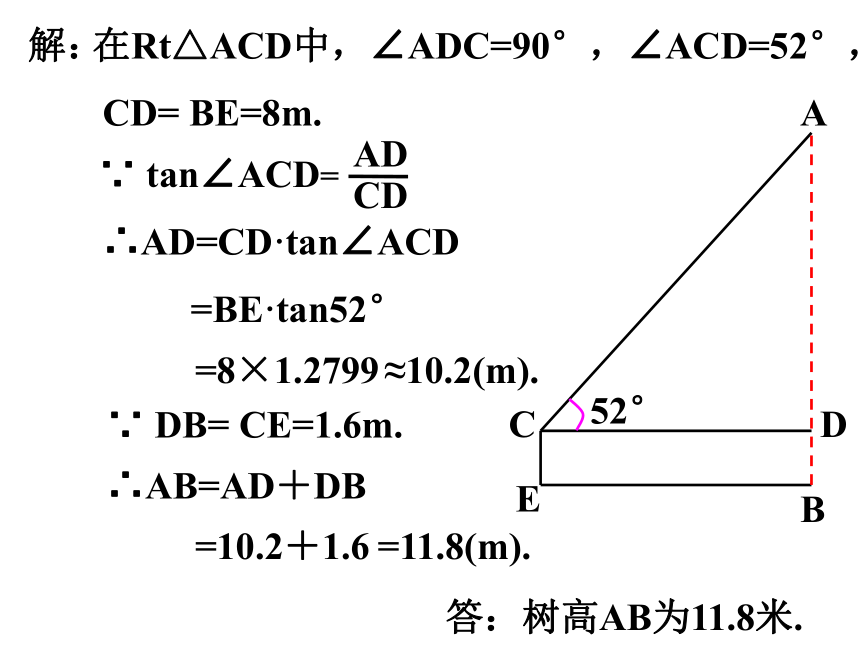
在Rt△ACD中,∠ADC=90°,∠ACD=52°,
AD
CD
CD= BE=8m.
∴AD=CD·tan∠ACD
=BE·tan52°
≈10.2(m).
=8×1.2799
∵ DB= CE=1.6m.
∴AB=AD+DB
=10.2+1.6
=11.8(m).
答:树高AB为11.8米.
1.如图,飞机的飞行高度AB=1000米,从飞机上测得地面着陆点C的俯角为18°,求飞机到着陆点的距离AC的值(精确到1m).
A
B
C
18°
解:
在Rt△ABC中,∠B=90°,∠C=18°,
AB=1000m
∵ sinC=
AB
AC
∴AC=
AB
sinC
=
1000
sin18°
=
1000
0.3090
≈3236(m).
答:飞机到着陆点的距离AC的值为3236m.
练习巩固
2. 如图,沿AC方向开山修路.为了加快施工进度,要在小山的另一侧的E处同时施工,如果从AC上的一点B取∠ABD = 140°,BD = 520m,∠D=50°,那么开挖点E离D多远,才能使点A,C,E正好成一直线(精确到1m).
50°
140°
520m
A
B
C
E
D
要求DE
要求∠E
要求cosD=
50°
140°
520m
A
B
C
E
D
∴∠E=∠ABD-∠D
答:开挖点E离点D 333m能使A,C,E正好成一直线.
解:要使A、C、E在同一直线上,则 ∠ABD是
△BDE 的一个外角.
∵cosD=
DE
BD
∴DE=BDcos50°
≈333.
=520×0.64
=140°-50°=90°.
在Rt△BED中,∠E=90°,∠D=50°,
由于仰角、俯角是视线与水平线所夹的角,因此当题目中已知仰角、俯角时,我们可以作出水平线,获得直角三角形,从而根据解直角三角形的知识求出线段长.
课堂小结
1.如图,从点C观测点D的仰角是( ).
A. ∠DAB B. ∠DCE
C. ∠DCA D. ∠ADC
A
B
C
D
E
巩固提高
B
2.如图,从点A处观测点B的仰角为40°,则从点B处观测点A的俯角为( ).
A. 30° B.40° C.50° D. 60°
A
B
40°
B
3.如图,在水平地面上,由点 A测得旗杆BC顶点C的仰角为60°,点A到旗杆的距离AB=12m,则旗杆的高度为( ).
A.6 m B.6m
C.12 m D.12 m
3
3
60°
A
B
C
C
4.如图,小亮为了测量校园里教学楼 AB 的高度,将测角仪CD 竖直放置在与教学楼水平距离为18 m的地面上.若测角仪的高度为1.5m,测得教学楼的顶部A处的仰角为30°,则教学楼AB的高度是( ).
A.55.5 m B.54 m
C. 19.5 m D. 18 m
A
B
C
D
30°
C
A
B
C
5.如图,从一栋二层楼的楼顶点A处看对面的教学楼,探测器显示,教学楼底部点C处的俯角为45°,楼顶部点D处的仰角为60°,且两栋楼之间的水平距离为6m,则教学楼的高CD是( ).
A.(6+6 )m
B.(6+3 )m
C.(6+2 )m
D. 12 m
3
3
3
A
6.如图,为了测量楼的高度,自楼的顶部A看地面上的一点B,俯角为 30°.已知地面上的这点与楼的水平距离BC为30m,那么楼的高度AC为 m(结果保留根号).
A
B
C
30°
3
10
7.如图,从位于塔顶的观测点C测得两建筑物底部A,B俯角分别为 45°和60°,此观测点C离地面的高度为51m,A,B两点在CD的两侧,且点A,B,D在同一水平直线上,则A,B之间的距离是 m(结果保留根号).
A
B
C
45°
60°
E
F
3)
17
(51+
8.如图,从甲楼的底部A处测得乙楼顶部C出的仰角为30°,从甲楼顶部B处测得乙楼D处的俯角时45°.已知甲楼的高是100m,则乙楼的高CD是 m.
A
B
C
30°
45°
D
3
100
3
应用解直角三角形的方法解决实际问题的一般步骤:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件,适当选用锐角三角函数解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
如果问题不能归结为一个直角三角形,则应当对所求的量进行分解,将其中的一部分量归结为直角三角形中的量.
今天作业
课本P131页第1、2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级上册
23.2 解直角三角形及其应用 (3)
仰角、俯角问题(1)
解直角三角形的理论在实际中的应用是学生在熟练掌握了勾股定理,直角三角形中两锐角互余,锐角三角函数,能利用直角三角形中的这些关系解直角三角形的基础上进行教学,主要应让学生学会用直角三角形的有关知识去解决某些简单的实际问题.它既是前面所学知识的运用,也是高中继续解斜三角形的重要预备知识.它的学习还蕴涵着深刻的数学思想方法(数学建模、转化化归),在本节教学中有针对性地对学生进行这方面的能力培养.
课件说明
教学目标: 1.使学生把仰角、俯角问题转化为解直角三角形问题,
从而会把实际问题转化为数学问题来解决,进一步
提高数学建模能力; 2.通过综合运用勾股定理,直角三角形的两个锐角互 余及锐角三角函数解直角三角形,逐步培养学生分 析问题、解决问题的能力.
教学重点: 将仰角、俯角问题中的数量关系,归结为直角三角形
元素之间的关系,从而利用所学知识解决实际题.
课件说明
(1)三边之间的关系
A
C
B
c
a
b
直角三角形各元素之间的关系
a2+b2=c2
(勾股定理)
(2)两锐角之间的关系
(3)边角之间的关系
∠A+∠B=90°
斜边
∠A的对边
a
c
sinA=
=
cosA=
斜边
∠A的邻边
=
b
c
tanA=
∠ A的邻边
∠A的对边
=
a
b
复习旧知
例3.如图,一学生要测量校园内一棵水杉树的高度,他站在距离水杉树8米的E处,测得树顶的仰角∠ACD=52°,已知测角器的架高CE=1.6m,问树高AB为多少米?(精确到0.1m).
A
B
E
C
D
52°
例题解析
铅直线
水平线
视线
视线
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;
仰角
从上往下看,视线与水平线的夹角叫做俯角.
俯角
学习新知
例3.如图,一学生要测量校园内一棵水杉树的高度,他站在距离水杉树8米的E处,测得树顶的仰角∠ACD=52°,已知测角器的架高CE=1.6m,问树高AB为多少米?(精确到0.1m).
A
B
E
C
D
52°
要求AB
要求AD
要求tan∠ACD=
例3.如图,一学生要测量校园内一棵水杉树的高度,他站在距离水杉树8米的E处,测得树顶的仰角∠ACD=52°,已知测角器的架高CE=1.6m,问树高AB为多少米?(精确到0.1m).
A
B
E
C
D
52°
∵ tan∠ACD=
解:
在Rt△ACD中,∠ADC=90°,∠ACD=52°,
AD
CD
CD= BE=8m.
∴AD=CD·tan∠ACD
=BE·tan52°
A
B
E
C
D
52°
∵ tan∠ACD=
解:
在Rt△ACD中,∠ADC=90°,∠ACD=52°,
AD
CD
CD= BE=8m.
∴AD=CD·tan∠ACD
=BE·tan52°
≈10.2(m).
=8×1.2799
∵ DB= CE=1.6m.
∴AB=AD+DB
=10.2+1.6
=11.8(m).
答:树高AB为11.8米.
1.如图,飞机的飞行高度AB=1000米,从飞机上测得地面着陆点C的俯角为18°,求飞机到着陆点的距离AC的值(精确到1m).
A
B
C
18°
解:
在Rt△ABC中,∠B=90°,∠C=18°,
AB=1000m
∵ sinC=
AB
AC
∴AC=
AB
sinC
=
1000
sin18°
=
1000
0.3090
≈3236(m).
答:飞机到着陆点的距离AC的值为3236m.
练习巩固
2. 如图,沿AC方向开山修路.为了加快施工进度,要在小山的另一侧的E处同时施工,如果从AC上的一点B取∠ABD = 140°,BD = 520m,∠D=50°,那么开挖点E离D多远,才能使点A,C,E正好成一直线(精确到1m).
50°
140°
520m
A
B
C
E
D
要求DE
要求∠E
要求cosD=
50°
140°
520m
A
B
C
E
D
∴∠E=∠ABD-∠D
答:开挖点E离点D 333m能使A,C,E正好成一直线.
解:要使A、C、E在同一直线上,则 ∠ABD是
△BDE 的一个外角.
∵cosD=
DE
BD
∴DE=BDcos50°
≈333.
=520×0.64
=140°-50°=90°.
在Rt△BED中,∠E=90°,∠D=50°,
由于仰角、俯角是视线与水平线所夹的角,因此当题目中已知仰角、俯角时,我们可以作出水平线,获得直角三角形,从而根据解直角三角形的知识求出线段长.
课堂小结
1.如图,从点C观测点D的仰角是( ).
A. ∠DAB B. ∠DCE
C. ∠DCA D. ∠ADC
A
B
C
D
E
巩固提高
B
2.如图,从点A处观测点B的仰角为40°,则从点B处观测点A的俯角为( ).
A. 30° B.40° C.50° D. 60°
A
B
40°
B
3.如图,在水平地面上,由点 A测得旗杆BC顶点C的仰角为60°,点A到旗杆的距离AB=12m,则旗杆的高度为( ).
A.6 m B.6m
C.12 m D.12 m
3
3
60°
A
B
C
C
4.如图,小亮为了测量校园里教学楼 AB 的高度,将测角仪CD 竖直放置在与教学楼水平距离为18 m的地面上.若测角仪的高度为1.5m,测得教学楼的顶部A处的仰角为30°,则教学楼AB的高度是( ).
A.55.5 m B.54 m
C. 19.5 m D. 18 m
A
B
C
D
30°
C
A
B
C
5.如图,从一栋二层楼的楼顶点A处看对面的教学楼,探测器显示,教学楼底部点C处的俯角为45°,楼顶部点D处的仰角为60°,且两栋楼之间的水平距离为6m,则教学楼的高CD是( ).
A.(6+6 )m
B.(6+3 )m
C.(6+2 )m
D. 12 m
3
3
3
A
6.如图,为了测量楼的高度,自楼的顶部A看地面上的一点B,俯角为 30°.已知地面上的这点与楼的水平距离BC为30m,那么楼的高度AC为 m(结果保留根号).
A
B
C
30°
3
10
7.如图,从位于塔顶的观测点C测得两建筑物底部A,B俯角分别为 45°和60°,此观测点C离地面的高度为51m,A,B两点在CD的两侧,且点A,B,D在同一水平直线上,则A,B之间的距离是 m(结果保留根号).
A
B
C
45°
60°
E
F
3)
17
(51+
8.如图,从甲楼的底部A处测得乙楼顶部C出的仰角为30°,从甲楼顶部B处测得乙楼D处的俯角时45°.已知甲楼的高是100m,则乙楼的高CD是 m.
A
B
C
30°
45°
D
3
100
3
应用解直角三角形的方法解决实际问题的一般步骤:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件,适当选用锐角三角函数解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
如果问题不能归结为一个直角三角形,则应当对所求的量进行分解,将其中的一部分量归结为直角三角形中的量.
今天作业
课本P131页第1、2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
