23.2 解直角三角形及其应用(4) 课件(共25张PPT)
文档属性
| 名称 | 23.2 解直角三角形及其应用(4) 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-06 10:51:40 | ||
图片预览



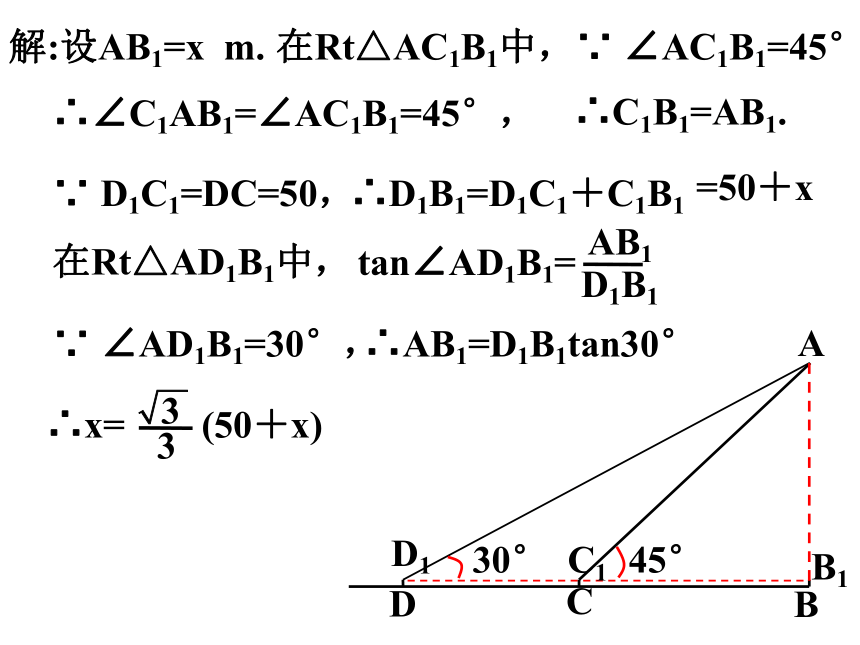
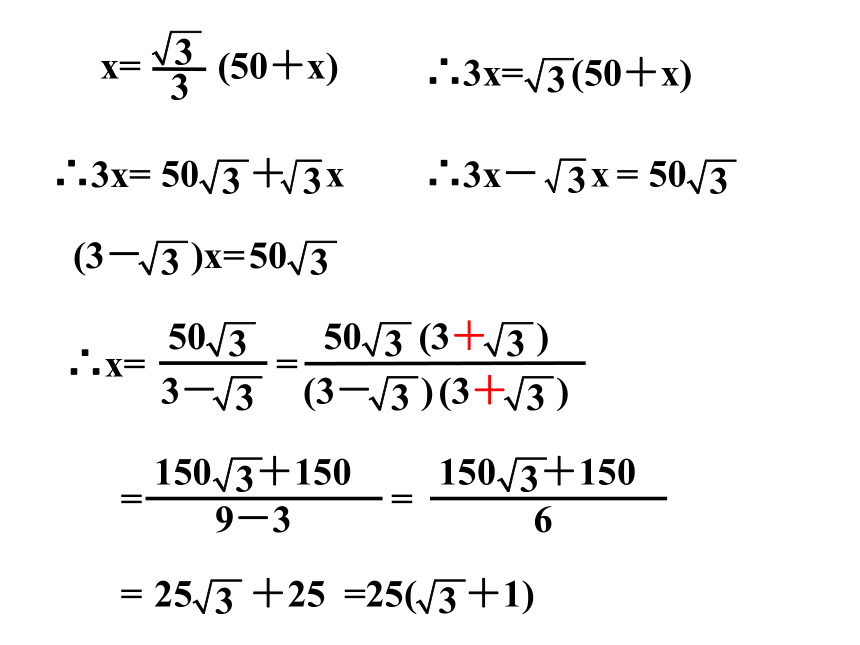

文档简介
(共25张PPT)
沪科版 九年级上册
23.2 解直角三角形及其应用 (4)
仰角、俯角问题(2)
教学目标: 1.使学生把仰角、俯角问题转化为解直角三角形问题,
从而会把实际问题转化为数学问题来解决,进一步
提高数学建模能力; 2.通过综合运用勾股定理,直角三角形的两个锐角互 余及锐角三角函数解直角三角形,逐步培养学生分 析问题、解决问题的能力.
教学重点: 将仰角、俯角问题中的数量关系,归结为直角三角形
元素之间的关系,从而利用所学知识解决实际题.
课件说明
已知条件 解法
一条边和一个锐角
斜边 c 和
锐角∠A
直角边 a 和锐角∠A
两条边
两条直角边
a 和 b
斜边 c 和直角边 a
∠B=90°-∠A,
∠B=90°-∠A,
a=csinA,
b=ccosA.
勾股求边,互余求角. 有斜用弦,
无斜用切. 取原避中,宁乘勿除.
tanA=
a
b
tanB=
b
a
sinA=
a
c
cosB=
a
c
tanA=
a
b
sinA=
a
c
复习旧知
A
B
E
C
D
52°
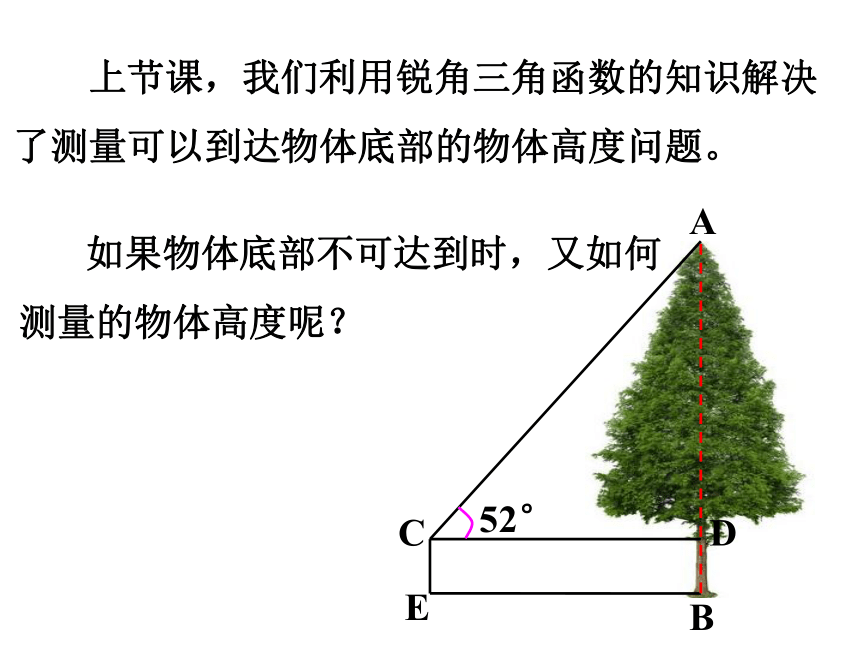
上节课,我们利用锐角三角函数的知识解决
了测量可以到达物体底部的物体高度问题。
如果物体底部不可达到时,又如何
测量的物体高度呢?
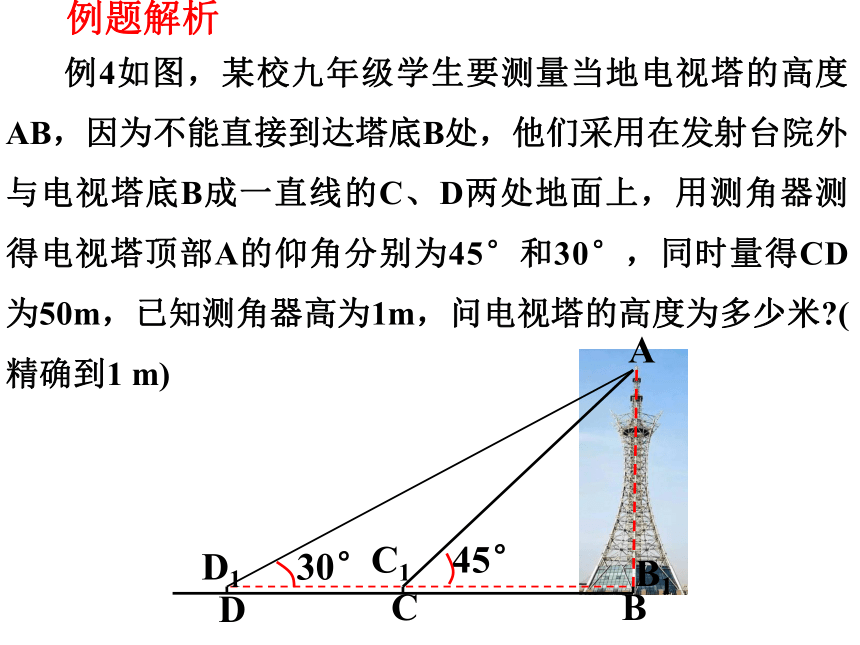
例4如图,某校九年级学生要测量当地电视塔的高度AB,因为不能直接到达塔底B处,他们采用在发射台院外与电视塔底B成一直线的C、D两处地面上,用测角器测得电视塔顶部A的仰角分别为45°和30°,同时量得CD为50m,已知测角器高为1m,问电视塔的高度为多少米 (精确到1 m)
A
B
C
D
45°
30°
D1
C1
B1
例题解析
A
B
C
D
45°
30°
D1
C1
B1
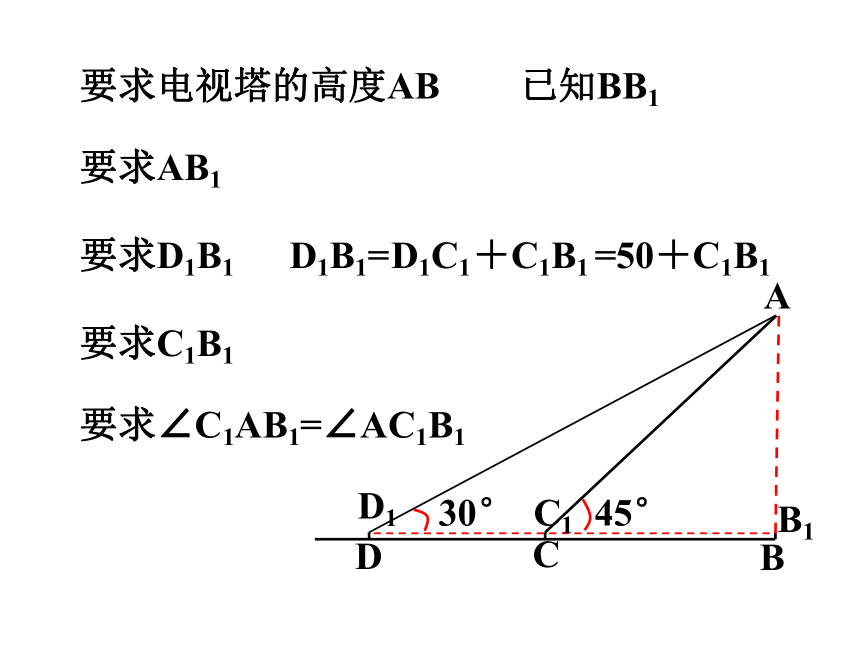
要求电视塔的高度AB
要求AB1
要求D1B1
已知BB1
D1B1=
D1C1
+C1B1
=50+C1B1
要求C1B1
要求∠C1AB1=∠AC1B1
A
B
C
D
45°
30°
D1
C1
B1
解:设AB1=x m.
在Rt△AC1B1中,∵ ∠AC1B1=45°,
∴∠C1AB1=∠AC1B1=45°,
∴C1B1=AB1.
∵ D1C1=DC=50,
∴D1B1=D1C1+C1B1
=50+x
在Rt△AD1B1中,
tan∠AD1B1=
AB1
D1B1
∵ ∠AD1B1=30°,
∴AB1=D1B1tan30°
∴x= (50+x)
3
3
x= (50+x)
3
3
∴3x= (50+x)
3
(3- )x=
3
∴x=
3
50
3
50
3-
3
∴3x=
3
50
+ x
3
∴3x- =
3
50
x
3
=
(3- )
3
(3+ )
3
3
50
(3+ )
3
=
9-3
3
150
+150
=
6
3
150
+150
=
3
25
+25
=25( +1)
3
A
B
C
D
45°
30°
D1
C1
B1
解:设AB1=x m.
在Rt△AC1B1中,∵ ∠AC1B1=45°,
∴∠C1AB1=∠AC1B1=45°,
∴C1B1=AB1.
∵ D1C1=DC=50,
∴D1B1=D1C1+C1B1
=50+x
在Rt△AD1B1中,
tan∠AD1B1=
AB1
D1B1
∵ ∠AD1B1=30°,
∴AB1=D1B1tan30°
∴x= (50+x),
3
3
∴x=25( +1)
3
∴AB=AB1+BB1
+1
=25( +1)
3
≈69(m).
答:电视塔的高度为69米.
A
B
C
D
45°
30°
D1
C1
B1
解:设AB1=x m.
在Rt△AC1B1中,∵ ∠AC1B1=45°,
∴∠C1AB1=∠AC1B1=45°,
∴C1B1=AB1.
∵ D1C1=DC=50,
∴D1B1=D1C1+C1B1
=50+x
在Rt△AD1B1中,
∵∠AD1B1=30°,
∴AD1=2AB1
=2x
∵ AD12=
D1B12+AB12
∴(2x)2=(50+x)2+x2
因测量得的仰角是特殊锐角,所以可有特殊解法
A
B
C
D
45°
30°
D1
C1
B1
∵ AD12=
D1B12+AB12
∴(2x)2=(50+x)2+x2
∴4x2=2500+100x+x2+x2
∴x2-50x-1250=0
∴x1=
=25( +1),
3
x2=
-25( -1)
3
(舍去)
∴2x2-100x-2500=0
∴x2-50x=1250
∴x2-50x+625=1250+625
∴(x-25)2=1875
∴x-25=
±
1875
∴x-25=
±
25
3
25
3
+25
A
B
C
D
45°
30°
D1
C1
B1
解:设AB1=x m.
在Rt△AC1B1中,∵ ∠AC1B1=45°,
∴∠C1AB1=∠AC1B1=45°,
∴C1B1=AB1.
∵ D1C1=DC=50,
∴D1B1=D1C1+C1B1
=50+x
在Rt△AD1B1中,
∵∠AD1B1=30°,
∴AD1=2AB1
=2x
∵ AD12=
D1B12+AB12
∴(2x)2=(50+x)2+x2
∴x1=
25( +1),
3
x2=
-25( -1)
3
(舍去)
∴AB=AB1+BB1
+1
≈69(m).
∴AB1= .
=25( +1)
3
25( +1)
3
1.如图,某直升机于空中A处测得正前方地面控制点C的俯角为30°;若航向不变,直升机继续向前飞行1000米至B处,测得地面控制点C的俯角为45°.求直升机再向前飞行远,与地面控制点C的距离最近?(结果保留根号).
45°
30°
A
B
C
练习巩固
45°
30°
A
B
C
D
解:如图.
过点C作CD垂直于AB于D.
设BD=x m,
在Rt△BCD中,∵ ∠CBD=45°,
∴∠BCD=∠CBD=45°,
∴BD=CD.
则CD=x m,
AD=(1000+x)m
在Rt△ACD中,
tan∠CAD=
CD
AD
∵∠CAD=30°,
∴CD=ADtan30°
∴x= (1000+x),
3
3
∴x=500( +1)
3
答:再向前飞行500( +1)m与地面控制点C的距离最近.
3
2.海上有一小岛,为了测量小岛两端A、B的距离,测量人员设计了一种测量方法,如图所示,已知B点是CD的中点,E是BA延长线上的一点,测得AE=8.3海里,DE=30海里,且DE⊥EC,cos∠D= .
(1)求小岛两端A、B的距离;
(2)过点C作CF⊥AB交AB的延长线于点F,
求sin∠BCF的值.
A
B
C
D
E
F
3
5
要求AB
要求BE
要求CD
解:(1)在Rt△CDE中,
(海里) .
A
B
C
D
E
F
∵ cos∠D =
DE
CD
∴
DE=30,
cos∠D =
3
5
30
CD
=
3
5
∴CD=50
∴BE= CD
∵B点是CD的中点,
1
2
=25
∴AB=
BE-AE
=25-8.3
=18.7
(2)在Rt△CDE中,由勾股定理得
A
B
C
D
E
F
∴BE= CD
1
2
=BC
∴∠BEC=∠BCE
∴cos∠BEC=cos∠BCE
∴
EF
EC
=
EC
CD
∴EF=
EC2
CD
=
402
50
=32
∴BF=
EF-BE
=32-25
=7
∴sin∠BCF =
BF
BC
=
7
25
EC2=
CD2-DE2
=502-302
∴EC=40.
=402,
要求BF
要求EF
要求CE
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;
(3)得到数学问题的解;
(4)得到实际问题的解.
1.如图,大楼外墙有高为AB 的广告牌,由距离大楼20 米的点 C(即CD=20米)观察它的顶部 A的仰角是55° ,底部B 的仰角是42° .则 AB的高度为 米.
参考数据:
C
D
B
A
sin55° ≈0.82,cos55° ≈0.57,tan55° ≈1.43;
sin42° ≈0.67,cos42° ≈0.74,tan42° ≈0.90.
10.6
巩固提高
2.如图,某景区有一处索道游览山谷的旅游点,已知索道两端距离AB为1300米,在山脚C点测得BC的距离为500米,∠ACB=90°,在C点观测山峰顶点A的仰角∠ACD=23.5°,则山峰AD的高度为 米.
(参考数据:sin23.5°≈0.40,cos23.5°=0.92,tan23.5°=0.43)
A
B
C
D
480
3.如图,某楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子CD=6m,坡脚到楼房的距离CB=8m.在D点处观察楼顶A点的仰角为54°,坡角∠DCE=30 .则楼房AB的高为 m. (结果精确0.1m).( , , , . )
E
A
B
C
D
30
54°
21.2
今天作业
课本P131页第3题
本节课在前面研究了解直角三角形的方法,通过例3、例4介绍了利用直角三角形中余弦、正切关系解决有关测量、建筑等方面的实际问题的基础上,结合“在航海中确定轮船距离灯塔有多远”的实际问题介绍解直角三角形的理论在实际中的应用,进一步领悟解直角三角形的知识也是解决实际问题的有效数学工具,在思想和方法上是提升.
课件说明
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级上册
23.2 解直角三角形及其应用 (4)
仰角、俯角问题(2)
教学目标: 1.使学生把仰角、俯角问题转化为解直角三角形问题,
从而会把实际问题转化为数学问题来解决,进一步
提高数学建模能力; 2.通过综合运用勾股定理,直角三角形的两个锐角互 余及锐角三角函数解直角三角形,逐步培养学生分 析问题、解决问题的能力.
教学重点: 将仰角、俯角问题中的数量关系,归结为直角三角形
元素之间的关系,从而利用所学知识解决实际题.
课件说明
已知条件 解法
一条边和一个锐角
斜边 c 和
锐角∠A
直角边 a 和锐角∠A
两条边
两条直角边
a 和 b
斜边 c 和直角边 a
∠B=90°-∠A,
∠B=90°-∠A,
a=csinA,
b=ccosA.
勾股求边,互余求角. 有斜用弦,
无斜用切. 取原避中,宁乘勿除.
tanA=
a
b
tanB=
b
a
sinA=
a
c
cosB=
a
c
tanA=
a
b
sinA=
a
c
复习旧知
A
B
E
C
D
52°
上节课,我们利用锐角三角函数的知识解决
了测量可以到达物体底部的物体高度问题。
如果物体底部不可达到时,又如何
测量的物体高度呢?
例4如图,某校九年级学生要测量当地电视塔的高度AB,因为不能直接到达塔底B处,他们采用在发射台院外与电视塔底B成一直线的C、D两处地面上,用测角器测得电视塔顶部A的仰角分别为45°和30°,同时量得CD为50m,已知测角器高为1m,问电视塔的高度为多少米 (精确到1 m)
A
B
C
D
45°
30°
D1
C1
B1
例题解析
A
B
C
D
45°
30°
D1
C1
B1
要求电视塔的高度AB
要求AB1
要求D1B1
已知BB1
D1B1=
D1C1
+C1B1
=50+C1B1
要求C1B1
要求∠C1AB1=∠AC1B1
A
B
C
D
45°
30°
D1
C1
B1
解:设AB1=x m.
在Rt△AC1B1中,∵ ∠AC1B1=45°,
∴∠C1AB1=∠AC1B1=45°,
∴C1B1=AB1.
∵ D1C1=DC=50,
∴D1B1=D1C1+C1B1
=50+x
在Rt△AD1B1中,
tan∠AD1B1=
AB1
D1B1
∵ ∠AD1B1=30°,
∴AB1=D1B1tan30°
∴x= (50+x)
3
3
x= (50+x)
3
3
∴3x= (50+x)
3
(3- )x=
3
∴x=
3
50
3
50
3-
3
∴3x=
3
50
+ x
3
∴3x- =
3
50
x
3
=
(3- )
3
(3+ )
3
3
50
(3+ )
3
=
9-3
3
150
+150
=
6
3
150
+150
=
3
25
+25
=25( +1)
3
A
B
C
D
45°
30°
D1
C1
B1
解:设AB1=x m.
在Rt△AC1B1中,∵ ∠AC1B1=45°,
∴∠C1AB1=∠AC1B1=45°,
∴C1B1=AB1.
∵ D1C1=DC=50,
∴D1B1=D1C1+C1B1
=50+x
在Rt△AD1B1中,
tan∠AD1B1=
AB1
D1B1
∵ ∠AD1B1=30°,
∴AB1=D1B1tan30°
∴x= (50+x),
3
3
∴x=25( +1)
3
∴AB=AB1+BB1
+1
=25( +1)
3
≈69(m).
答:电视塔的高度为69米.
A
B
C
D
45°
30°
D1
C1
B1
解:设AB1=x m.
在Rt△AC1B1中,∵ ∠AC1B1=45°,
∴∠C1AB1=∠AC1B1=45°,
∴C1B1=AB1.
∵ D1C1=DC=50,
∴D1B1=D1C1+C1B1
=50+x
在Rt△AD1B1中,
∵∠AD1B1=30°,
∴AD1=2AB1
=2x
∵ AD12=
D1B12+AB12
∴(2x)2=(50+x)2+x2
因测量得的仰角是特殊锐角,所以可有特殊解法
A
B
C
D
45°
30°
D1
C1
B1
∵ AD12=
D1B12+AB12
∴(2x)2=(50+x)2+x2
∴4x2=2500+100x+x2+x2
∴x2-50x-1250=0
∴x1=
=25( +1),
3
x2=
-25( -1)
3
(舍去)
∴2x2-100x-2500=0
∴x2-50x=1250
∴x2-50x+625=1250+625
∴(x-25)2=1875
∴x-25=
±
1875
∴x-25=
±
25
3
25
3
+25
A
B
C
D
45°
30°
D1
C1
B1
解:设AB1=x m.
在Rt△AC1B1中,∵ ∠AC1B1=45°,
∴∠C1AB1=∠AC1B1=45°,
∴C1B1=AB1.
∵ D1C1=DC=50,
∴D1B1=D1C1+C1B1
=50+x
在Rt△AD1B1中,
∵∠AD1B1=30°,
∴AD1=2AB1
=2x
∵ AD12=
D1B12+AB12
∴(2x)2=(50+x)2+x2
∴x1=
25( +1),
3
x2=
-25( -1)
3
(舍去)
∴AB=AB1+BB1
+1
≈69(m).
∴AB1= .
=25( +1)
3
25( +1)
3
1.如图,某直升机于空中A处测得正前方地面控制点C的俯角为30°;若航向不变,直升机继续向前飞行1000米至B处,测得地面控制点C的俯角为45°.求直升机再向前飞行远,与地面控制点C的距离最近?(结果保留根号).
45°
30°
A
B
C
练习巩固
45°
30°
A
B
C
D
解:如图.
过点C作CD垂直于AB于D.
设BD=x m,
在Rt△BCD中,∵ ∠CBD=45°,
∴∠BCD=∠CBD=45°,
∴BD=CD.
则CD=x m,
AD=(1000+x)m
在Rt△ACD中,
tan∠CAD=
CD
AD
∵∠CAD=30°,
∴CD=ADtan30°
∴x= (1000+x),
3
3
∴x=500( +1)
3
答:再向前飞行500( +1)m与地面控制点C的距离最近.
3
2.海上有一小岛,为了测量小岛两端A、B的距离,测量人员设计了一种测量方法,如图所示,已知B点是CD的中点,E是BA延长线上的一点,测得AE=8.3海里,DE=30海里,且DE⊥EC,cos∠D= .
(1)求小岛两端A、B的距离;
(2)过点C作CF⊥AB交AB的延长线于点F,
求sin∠BCF的值.
A
B
C
D
E
F
3
5
要求AB
要求BE
要求CD
解:(1)在Rt△CDE中,
(海里) .
A
B
C
D
E
F
∵ cos∠D =
DE
CD
∴
DE=30,
cos∠D =
3
5
30
CD
=
3
5
∴CD=50
∴BE= CD
∵B点是CD的中点,
1
2
=25
∴AB=
BE-AE
=25-8.3
=18.7
(2)在Rt△CDE中,由勾股定理得
A
B
C
D
E
F
∴BE= CD
1
2
=BC
∴∠BEC=∠BCE
∴cos∠BEC=cos∠BCE
∴
EF
EC
=
EC
CD
∴EF=
EC2
CD
=
402
50
=32
∴BF=
EF-BE
=32-25
=7
∴sin∠BCF =
BF
BC
=
7
25
EC2=
CD2-DE2
=502-302
∴EC=40.
=402,
要求BF
要求EF
要求CE
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;
(3)得到数学问题的解;
(4)得到实际问题的解.
1.如图,大楼外墙有高为AB 的广告牌,由距离大楼20 米的点 C(即CD=20米)观察它的顶部 A的仰角是55° ,底部B 的仰角是42° .则 AB的高度为 米.
参考数据:
C
D
B
A
sin55° ≈0.82,cos55° ≈0.57,tan55° ≈1.43;
sin42° ≈0.67,cos42° ≈0.74,tan42° ≈0.90.
10.6
巩固提高
2.如图,某景区有一处索道游览山谷的旅游点,已知索道两端距离AB为1300米,在山脚C点测得BC的距离为500米,∠ACB=90°,在C点观测山峰顶点A的仰角∠ACD=23.5°,则山峰AD的高度为 米.
(参考数据:sin23.5°≈0.40,cos23.5°=0.92,tan23.5°=0.43)
A
B
C
D
480
3.如图,某楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子CD=6m,坡脚到楼房的距离CB=8m.在D点处观察楼顶A点的仰角为54°,坡角∠DCE=30 .则楼房AB的高为 m. (结果精确0.1m).( , , , . )
E
A
B
C
D
30
54°
21.2
今天作业
课本P131页第3题
本节课在前面研究了解直角三角形的方法,通过例3、例4介绍了利用直角三角形中余弦、正切关系解决有关测量、建筑等方面的实际问题的基础上,结合“在航海中确定轮船距离灯塔有多远”的实际问题介绍解直角三角形的理论在实际中的应用,进一步领悟解直角三角形的知识也是解决实际问题的有效数学工具,在思想和方法上是提升.
课件说明
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
