23.2 解直角三角形及其应用(1) 课件(共25张PPT)
文档属性
| 名称 | 23.2 解直角三角形及其应用(1) 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-06 10:54:21 | ||
图片预览






文档简介
(共25张PPT)
沪科版 九年级上册
23.2 解直角三角形及其应用 (1)
本节课是在学习锐角三角函数之后,结合已学过的勾股定理和三角形内角和定理,研究解直角三角形的方法.本节课既帮助学生进一步理解锐角三角函数的概念,同时又为以后的应用举例打下基础.
课件说明
教学目标: 1.了解解直角三角形的意义和条件; 2.能根据已知的两个条件(至少有一个是边), 解直角三角形.
教学重点:解直角三角形的依据和方法.
教学难点:根据不同的已知条件,相应的解直角三角形.
课件说明
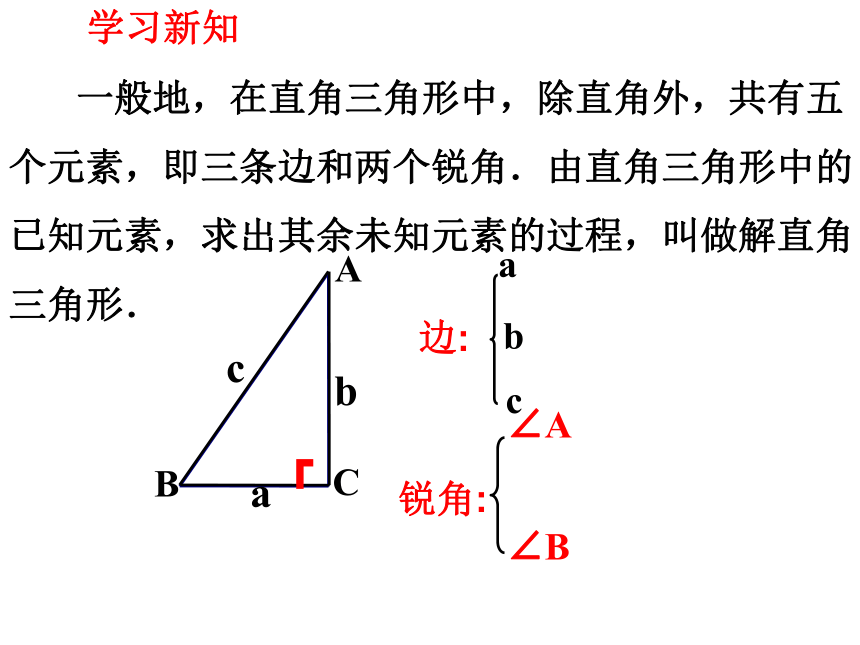
一般地,在直角三角形中,除直角外,共有五个元素,即三条边和两个锐角.由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
B
a
C
b
A
c
┏
边:
锐角:
a
b
c
∠B
∠A
学习新知
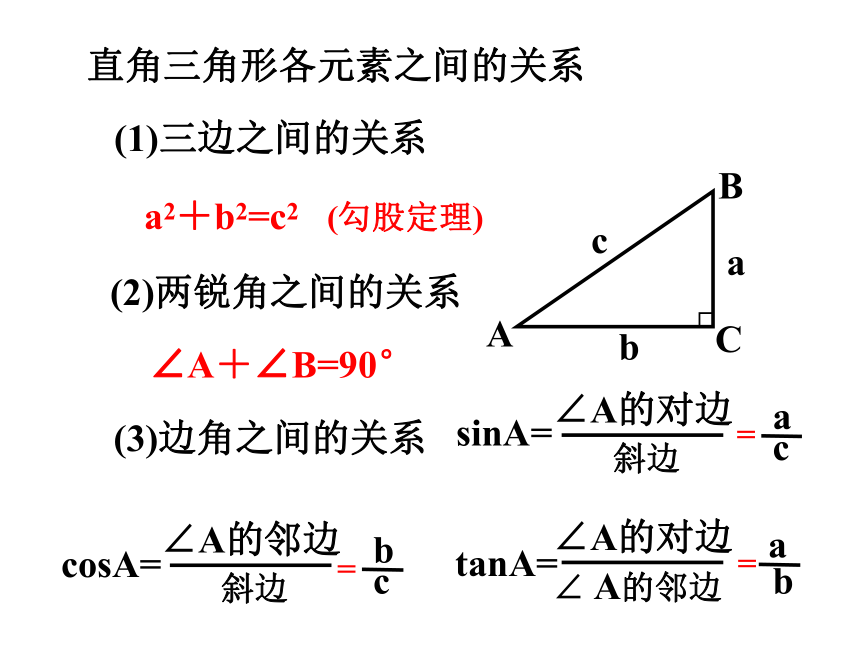
(1)三边之间的关系
A
C
B
c
a
b
直角三角形各元素之间的关系
a2+b2=c2
(勾股定理)
(2)两锐角之间的关系
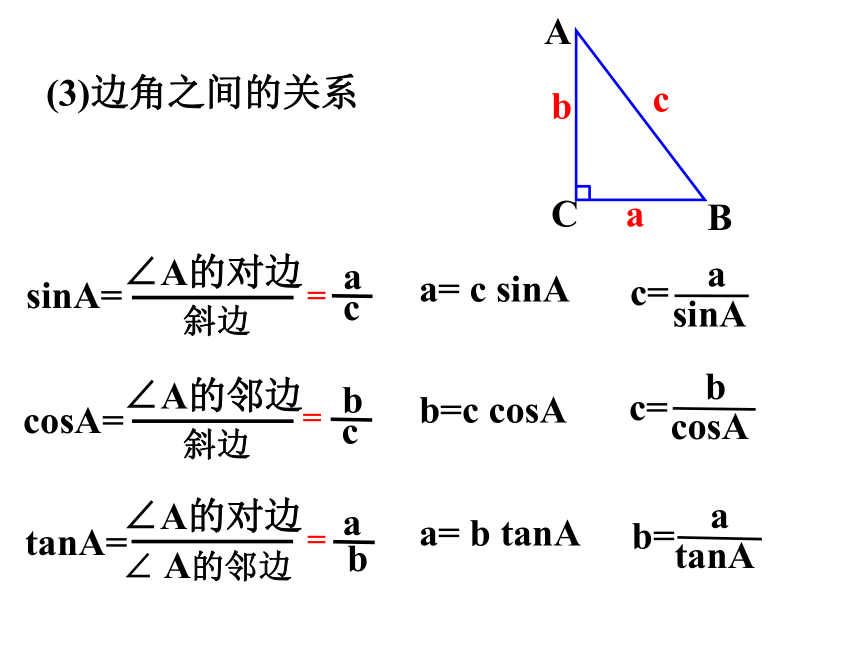
(3)边角之间的关系
∠A+∠B=90°
斜边
∠A的对边
a
c
sinA=
=
cosA=
斜边
∠A的邻边
=
b
c
tanA=
∠ A的邻边
∠A的对边
=
a
b
一般地,在直角三角形中,除直角外,共有五个元 素,即三条边和两个锐角.由直角三角形中的已知元素, 求出其余未知元素的过程,叫做解直角三角形.
B
a
C
b
A
c
┏
边:
锐角:
a
b
c
∠B
∠A
在直角三角形中,知道五个元素中的两个元素(至少有一个是边) ,可以求其余元素.
A
B
a
b
c
C
(1)三边之间的关系
a2+b2=c2
(勾股定理)
在解直角三角形的过程中,一般要用到下面一些关系
(2)两锐角之间的关系
∠A+∠B=90°
∠A=90° -∠B
∠B=90°- ∠A
在解直角三角形的过程中,一般要用到下面一些关系
A
B
a
b
c
C
(3)边角之间的关系
a= c sinA
b=c cosA
a= b tanA
A
B
a
b
c
C
斜边
∠A的对边
a
c
sinA=
=
c=
sinA
a
cosA=
斜边
∠A的邻边
=
b
c
c=
cosA
b
tanA=
∠ A的邻边
∠A的对边
=
a
b
b=
tanA
a
例 在Rt△ABC中,∠C=90°,c =30 , b =20,
A
B
C
b=20
a
c=30
解这个直角三角形.
例题解析
本题已知斜边长c和直角边长 b,
可以根据勾股定理求出另一直角边长 a,
再利用三角函数关系求出两个锐角∠ A, ∠ B.
分析 :
例 在Rt△ABC中,∠C=90°,c =30 , b =20,
A
B
C
b=20
a
c=30
解这个直角三角形.
∵c=30,b=20,
解:
∴a2=c2-b2=302-202=500,
∴a=
∵sinB=
∴∠B=41°48′37″,
∴∠A=90°- ∠B
10
5
b
c
=
30
20
≈0.6667,
=48°11′23″.
例题解析
例1 在Rt△ABC中,∠C=90°,∠B=42°6′,
c=287.4, 解这个直角三角形(精确到0.1).
A
B
C
解:
∵sinB=
∴∠A=90°-∠B
∵ ∠C=90°,∠B=42°6′,
=90°-42°6′
=47°54′
b
c
∴b= c sinB
=287.4×0.6704
≈192.7.
∵cosB=
a
c
∴a= c cosB
=287.4×0.7420
≈213.3.
练习巩固
1.根据下列条件,解直角三角形:
(1)在Rt△ABC中,∠C=90°,a = 30,∠B=80°.
(2)在Rt△ABC中,∠C=90°,c = 8,b=3.
(3)在Rt△ABC中,∠C=90°,c = 10,∠A=40°.
1.根据下列条件,解直角三角形:
A
B
C
b
c
a=30
(1)在Rt△ABC中,∠C=90°,a = 30,∠B=80°.
∵∠B=80°,
解:
∴∠A=90°- ∠B=90°-80°=10°.
∵tanB=
∴b=atan80°
b
a
≈170.1,
∵cosB=
a
c
=30×5.671
∴
c=
cos80°
a
=
0.1736
30
≈172.8.
A
B
C
b=20
a
c=30
∵c=8,b=3,
解:
∴a2=c2-b2=82-32=55,
∴a=
∵sinB=
∴∠B=22°01′28″,
∴∠A=90°- ∠B
55
b
c
=
8
3
=0.375,
=67°58′32″.
1.根据下列条件,解直角三角形:
(2)在Rt△ABC中,∠C=90°,c = 8,b=3.
1.根据下列条件,解直角三角形:
A
B
C
b
c=10
a
(3)在Rt△ABC中,∠C=90°,c = 10,∠A=40°.
∵∠A=40°,
解:
∴∠B=90°- ∠A=90°-40°=50°.
∵sinA=
∴a=csin40°
a
c
≈6.43,
∵cosA=
b
c
=10×0.6427
∴b=ccos40°
≈7.66.
=10×0.7660
1.什么叫解直角三角形? 直角三角形中,除直角外,五个元素之间有怎样的关系?
2.两个直角三角形全等要具备什么条件?为什么在直角三角形中,已知一条边和一个锐角,或两边,就能解这个直角三角形?
3.你能根据不同的已知条件,归纳相应的解直角三角形的方法吗?
课堂小结
1.如图,在Rt△ABC中,∠C=90°,AB=10 ,
∠ B=40°.则AC的长是( ).
A. 10cos 40° B.10sin 40°
C. 10tan 40° D.
sin 40°
10
A
B
C
10
B
巩固提高
2.如图,在Rt△ABC中,∠C=90° ,则
下列结论正确的是( ).
A.AC=BC·tan A B.AB=AC·cosA
C.AC=AB·sin A D.AC=BC·tan B
A
B
C
D
3.在Rt△ABC中,∠C=90° ,AC=2,
cos A= ,则AB 的长是( ).
A. B. C. D.
4
3
2
5
3
8
3
10
3
2
7
A
B
C
2
B
4.在Rt△ABC中,∠C=90° sinA= ,
AC=6cm,则BC的长度为( ).
A.6 cm B.7 cm C.8 cm D.9 cm
5
4
C
5.在Rt△ABC中,∠C=90° , ∠ A=45°,
AB=2 ,则AC= .
6.在Rt△ABC中,∠C=90° , ∠A=30°,
BC=4.则AB= ,AC= .
2
2
8
3
4
今天作业
课本P125页第2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级上册
23.2 解直角三角形及其应用 (1)
本节课是在学习锐角三角函数之后,结合已学过的勾股定理和三角形内角和定理,研究解直角三角形的方法.本节课既帮助学生进一步理解锐角三角函数的概念,同时又为以后的应用举例打下基础.
课件说明
教学目标: 1.了解解直角三角形的意义和条件; 2.能根据已知的两个条件(至少有一个是边), 解直角三角形.
教学重点:解直角三角形的依据和方法.
教学难点:根据不同的已知条件,相应的解直角三角形.
课件说明
一般地,在直角三角形中,除直角外,共有五个元素,即三条边和两个锐角.由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
B
a
C
b
A
c
┏
边:
锐角:
a
b
c
∠B
∠A
学习新知
(1)三边之间的关系
A
C
B
c
a
b
直角三角形各元素之间的关系
a2+b2=c2
(勾股定理)
(2)两锐角之间的关系
(3)边角之间的关系
∠A+∠B=90°
斜边
∠A的对边
a
c
sinA=
=
cosA=
斜边
∠A的邻边
=
b
c
tanA=
∠ A的邻边
∠A的对边
=
a
b
一般地,在直角三角形中,除直角外,共有五个元 素,即三条边和两个锐角.由直角三角形中的已知元素, 求出其余未知元素的过程,叫做解直角三角形.
B
a
C
b
A
c
┏
边:
锐角:
a
b
c
∠B
∠A
在直角三角形中,知道五个元素中的两个元素(至少有一个是边) ,可以求其余元素.
A
B
a
b
c
C
(1)三边之间的关系
a2+b2=c2
(勾股定理)
在解直角三角形的过程中,一般要用到下面一些关系
(2)两锐角之间的关系
∠A+∠B=90°
∠A=90° -∠B
∠B=90°- ∠A
在解直角三角形的过程中,一般要用到下面一些关系
A
B
a
b
c
C
(3)边角之间的关系
a= c sinA
b=c cosA
a= b tanA
A
B
a
b
c
C
斜边
∠A的对边
a
c
sinA=
=
c=
sinA
a
cosA=
斜边
∠A的邻边
=
b
c
c=
cosA
b
tanA=
∠ A的邻边
∠A的对边
=
a
b
b=
tanA
a
例 在Rt△ABC中,∠C=90°,c =30 , b =20,
A
B
C
b=20
a
c=30
解这个直角三角形.
例题解析
本题已知斜边长c和直角边长 b,
可以根据勾股定理求出另一直角边长 a,
再利用三角函数关系求出两个锐角∠ A, ∠ B.
分析 :
例 在Rt△ABC中,∠C=90°,c =30 , b =20,
A
B
C
b=20
a
c=30
解这个直角三角形.
∵c=30,b=20,
解:
∴a2=c2-b2=302-202=500,
∴a=
∵sinB=
∴∠B=41°48′37″,
∴∠A=90°- ∠B
10
5
b
c
=
30
20
≈0.6667,
=48°11′23″.
例题解析
例1 在Rt△ABC中,∠C=90°,∠B=42°6′,
c=287.4, 解这个直角三角形(精确到0.1).
A
B
C
解:
∵sinB=
∴∠A=90°-∠B
∵ ∠C=90°,∠B=42°6′,
=90°-42°6′
=47°54′
b
c
∴b= c sinB
=287.4×0.6704
≈192.7.
∵cosB=
a
c
∴a= c cosB
=287.4×0.7420
≈213.3.
练习巩固
1.根据下列条件,解直角三角形:
(1)在Rt△ABC中,∠C=90°,a = 30,∠B=80°.
(2)在Rt△ABC中,∠C=90°,c = 8,b=3.
(3)在Rt△ABC中,∠C=90°,c = 10,∠A=40°.
1.根据下列条件,解直角三角形:
A
B
C
b
c
a=30
(1)在Rt△ABC中,∠C=90°,a = 30,∠B=80°.
∵∠B=80°,
解:
∴∠A=90°- ∠B=90°-80°=10°.
∵tanB=
∴b=atan80°
b
a
≈170.1,
∵cosB=
a
c
=30×5.671
∴
c=
cos80°
a
=
0.1736
30
≈172.8.
A
B
C
b=20
a
c=30
∵c=8,b=3,
解:
∴a2=c2-b2=82-32=55,
∴a=
∵sinB=
∴∠B=22°01′28″,
∴∠A=90°- ∠B
55
b
c
=
8
3
=0.375,
=67°58′32″.
1.根据下列条件,解直角三角形:
(2)在Rt△ABC中,∠C=90°,c = 8,b=3.
1.根据下列条件,解直角三角形:
A
B
C
b
c=10
a
(3)在Rt△ABC中,∠C=90°,c = 10,∠A=40°.
∵∠A=40°,
解:
∴∠B=90°- ∠A=90°-40°=50°.
∵sinA=
∴a=csin40°
a
c
≈6.43,
∵cosA=
b
c
=10×0.6427
∴b=ccos40°
≈7.66.
=10×0.7660
1.什么叫解直角三角形? 直角三角形中,除直角外,五个元素之间有怎样的关系?
2.两个直角三角形全等要具备什么条件?为什么在直角三角形中,已知一条边和一个锐角,或两边,就能解这个直角三角形?
3.你能根据不同的已知条件,归纳相应的解直角三角形的方法吗?
课堂小结
1.如图,在Rt△ABC中,∠C=90°,AB=10 ,
∠ B=40°.则AC的长是( ).
A. 10cos 40° B.10sin 40°
C. 10tan 40° D.
sin 40°
10
A
B
C
10
B
巩固提高
2.如图,在Rt△ABC中,∠C=90° ,则
下列结论正确的是( ).
A.AC=BC·tan A B.AB=AC·cosA
C.AC=AB·sin A D.AC=BC·tan B
A
B
C
D
3.在Rt△ABC中,∠C=90° ,AC=2,
cos A= ,则AB 的长是( ).
A. B. C. D.
4
3
2
5
3
8
3
10
3
2
7
A
B
C
2
B
4.在Rt△ABC中,∠C=90° sinA= ,
AC=6cm,则BC的长度为( ).
A.6 cm B.7 cm C.8 cm D.9 cm
5
4
C
5.在Rt△ABC中,∠C=90° , ∠ A=45°,
AB=2 ,则AC= .
6.在Rt△ABC中,∠C=90° , ∠A=30°,
BC=4.则AB= ,AC= .
2
2
8
3
4
今天作业
课本P125页第2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
