23.2 解直角三角形及其应用(6) 课件(共25张PPT)
文档属性
| 名称 | 23.2 解直角三角形及其应用(6) 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-06 00:00:00 | ||
图片预览




文档简介
(共25张PPT)
沪科版 九年级上册
23.2 解直角三角形及其应用 (6)
坡度、坡角问题
教学目标:
1.使学生把坡度、坡角问题转化为解直角三角形问题,
从而 会把实际问题转化为数学问题来解决,进一步
提高数学建模能力;
2.通过综合运用勾股定理,直角三角形的两个锐角互
余及锐角三角函数解直角三角形,逐步培养学生分
析问题、解决问题的能力.
教学重点:
将坡度、坡角问题中的数量关系,归结为直角三角形
元素之间的关系,从而利用所学知识解决实际题.
课件说明
l
h
α
i=h:l
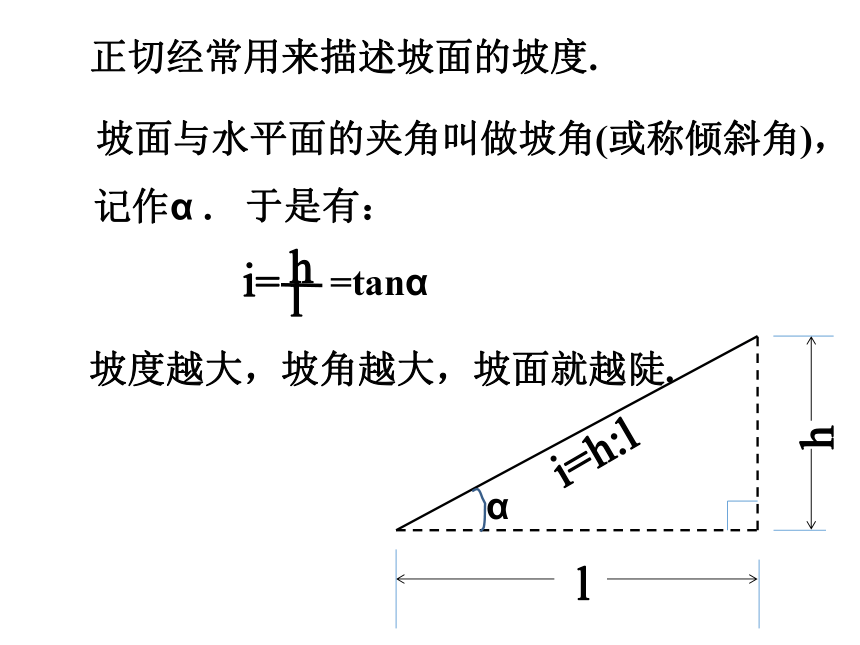
正切经常用来描述坡面的坡度.
坡面的铅直高度h和水平长度l 的比叫做坡面的坡度.
i=
h
l
(坡度通常写成h:l 的形式)
记作i .
复习旧知
l
h
α
i=h:l
正切经常用来描述坡面的坡度.
坡面与水平面的夹角叫做坡角(或称倾斜角),
i=
h
l
=tanα
坡度越大,坡角越大,坡面就越陡.
于是有:
记作α .
2.如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的坡度为2: 5 ,则此斜坡的水平距离 m.
A
B
75
C
2: 5=
30: x
2x=150
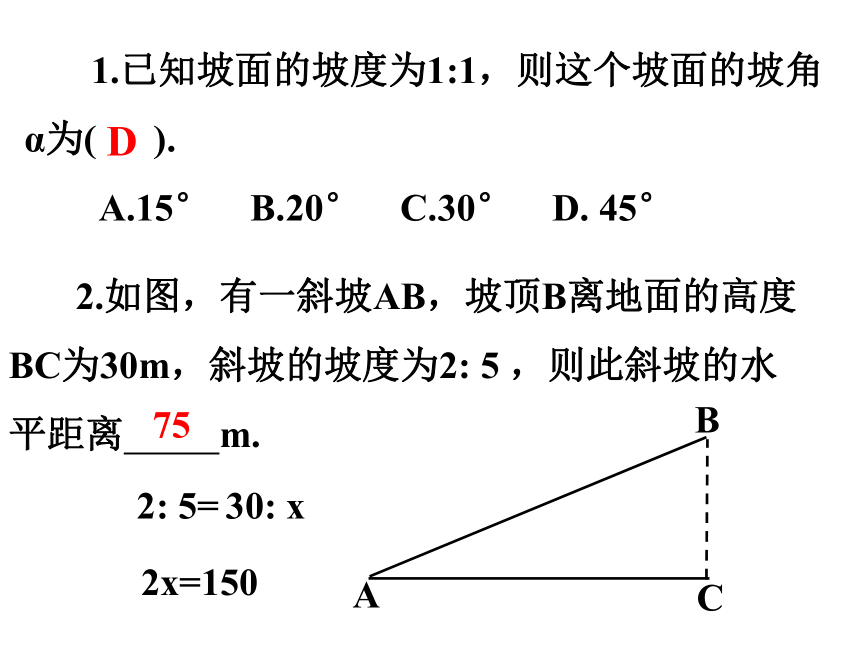
1.已知坡面的坡度为1:1,则这个坡面的坡角 α为( ).
A.15° B.20° C.30° D. 45°
D
3.如图,一山坡面的坡度为i=1: ,则这个山坡的坡角度数为 . 小辰从山脚A出发,沿山坡向上走了200m到达点B,则小辰上升了 m.
3
A
B
30°
100
C
∵tan∠A=
i=1:
1
=
3
=
3
tan30°=
3
3
3
3
∠A=
30°
4.如图,一名滑雪运动员沿着坡角为34°的斜坡, 从A滑行至B,已知AB=500m,则这名滑雪运动员的高度下降了 m.
(参考数据:sin34°≈0.56,cos34°≈0.83,
tan34°≈0.67)
B
A
C
34°
∵sin34°=
AC
AB
∴AC=500sin34°
≈500×0.56
280
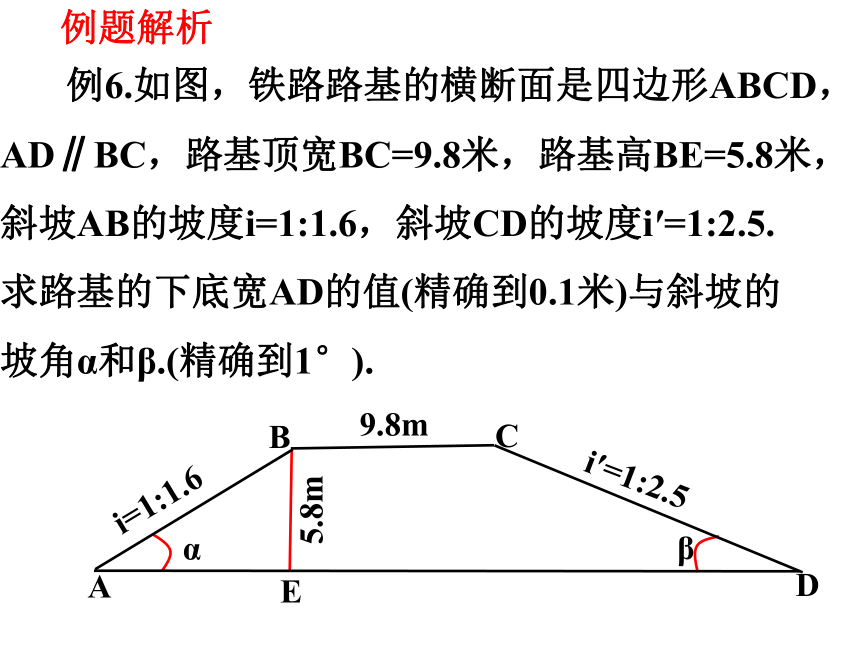
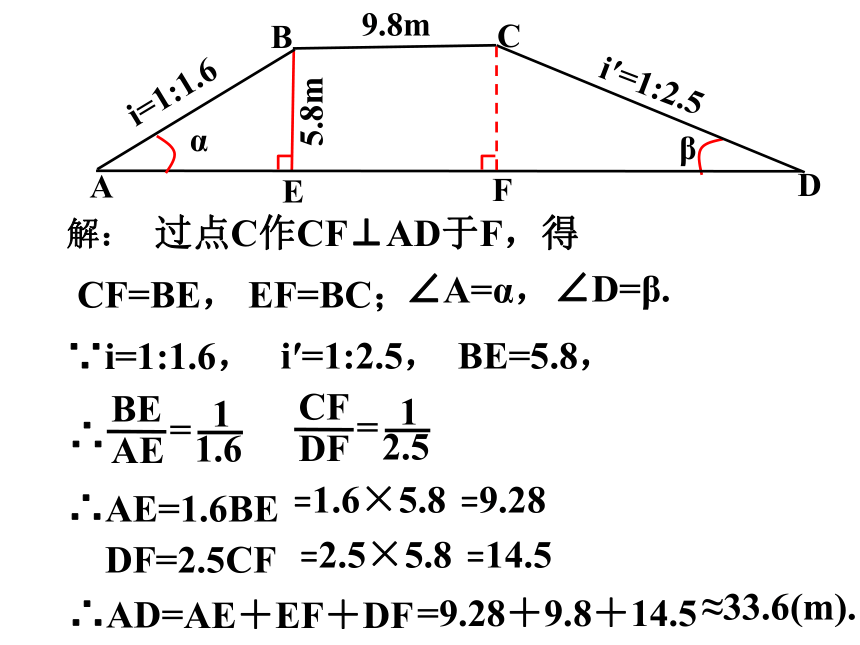
例6.如图,铁路路基的横断面是四边形ABCD,AD∥BC,路基顶宽BC=9.8米,路基高BE=5.8米,斜坡AB的坡度i=1:1.6,斜坡CD的坡度i′=1:2.5.求路基的下底宽AD的值(精确到0.1米)与斜坡的坡角α和β.(精确到1°).
B
A
D
E
C
9.8m
α
β
i′=1:2.5
i=1:1.6
5.8m
例题解析
B
A
D
E
C
9.8m
α
β
i′=1:2.5
i=1:1.6
5.8m
F
过点C作CF⊥AD于F,得
解:
CF=BE,
EF=BC;
∠A=α,
∠D=β.
∵i=1:1.6,
i′=1:2.5,
BE
AE
=
1
1.6
BE=5.8,
∴
CF
DF
=
1
2.5
∴AE=1.6BE
=1.6×5.8
=9.28
DF=2.5CF
=2.5×5.8
=14.5
∴AD=
AE+EF+DF
=9.28+9.8+14.5
≈33.6(m).
B
A
D
E
C
9.8m
α
β
i′=1:2.5
i=1:1.6
5.8m
F
在Rt△ABE中,
∵tanα=
BE
AE
=
i=1:1.6
=
5
8
∴α≈32°;
=0.625,
在Rt△DCF中,
∵tanβ=
CF
DF
=
i′=1:2.5
=
2
5
∴β≈22°.
=0.4,
答:路基的下底宽为33.6m,
斜坡的坡角分别为32°和22°.
1.如图,水库大坝的横断面是四边形ABCD,BC∥AD,坝顶宽为6m,坝高为23m,斜坡AB的坡度i=1:3,斜坡CD的坡度i′=1:2.5.求:
(1)斜坡AB的坡角α的值.(精确到1°).
(2)坝底宽AD和斜坡AB的值(精确到0.1m)
B
A
D
E
C
6m
α
β
i′=1:2.5
i=1:3
23m
练习巩固
B
A
D
E
C
6m
α
β
i′=1:2.5
i=1:3
∵tanα=
i=1:3
1
3
∴α=18°;
≈0.3333,
解:(1)
=
B
A
D
E
C
6m
α
i′=1:2.5
i=1:3
23m
F
过点C作CF⊥AD于F,得
CF=BE,
EF=BC;
∵i=1:3,
i′=1:2.5,
BE
AE
=
1
3
BE=23,
∴
CF
DF
=
1
2.5
∴AE=3BE
=3×23
=69
DF=2.5CF
=2.5×23
=57.5
∴AD=
AE+EF+DF
=69+6+57.5
=132.5(m).
(2)
B
A
D
E
C
6m
α
β
i′=1:2.5
i=1:3
23m
∵BE=23,
AE=3BE=69,
∴AB2=
AE2+BE2
=692+232
∴AB=
10
23
=232 (32+1)
≈72.7(m).
B
A
D
E
C
6m
α
β
i′=1:2.5
i=1:3
23m
在Rt△ABE中,∠α=18°,
∵sinα=
BE
AB
=
0.31
23
∴AB=
sin18°
BE
≈72.7(m).
2.如图,燕尾槽的横断面是四边形ABCD,AD∥BC,其中∠B=∠C=55°,外口宽AD=180mm,燕尾槽的深度AE=70mm.求它的里口宽BC的值 .(精确到1mm).
E
D
C
B
A
E
D
C
B
A
过点D作DF⊥BC于F.
解:
F
∵ AD∥BC,
AE⊥BC
∴AE=DF,
∵ ∠B=∠C=55°,
∴△ABE≌△DFC.
∴BE=CF.
AD=EF.
在Rt△ABE中,
tan∠B=
AE
BE
∴BE=
AE
tan∠B
=
70
tan55°
=
70
1.43
≈49(mm).
∴BC=
BE+EF+CF
=49+180+49
=278(mm).
答:里口宽BC的值为278mm .
对于坡度、坡角问题,解题的关键是将坡度转化为线段的比,并寻找或构造合适的直角三角形.
课堂小结
1.如图,某山坡的坡面AB=200m,坡角∠BAC=30°,则该山坡的高BC为 m.
A
B
C
30°
巩固提高
100
2.如图,斜坡AB的坡度i=1:3,该斜坡的水平距离AC=6m,则斜坡AB的长为 m.
A
B
C
10
2
i=1:3
6
2
3.如图,某村准备在坡度为1:2的山坡上栽树,要求相邻两棵树之间的水平距离AC为4m,则这两棵树在坡面上的距离AB为 m.
A
B
C
4m
5
2
4.如图,小林从点A出发,沿着坡角为 α的斜坡向上走了650m到达点B,且sinα= .然后又沿着坡度i=1:3的斜坡向上走了500m到达点C.
(1)小林从点A到达点B的高度是 米;
(2)小林从点A到达点C上升的高度CD
是 米.
A
B
C
D
E
α
i=1:3
4
13
200
F
10 )
50
( 200+
今天作业
课本P131页第5题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级上册
23.2 解直角三角形及其应用 (6)
坡度、坡角问题
教学目标:
1.使学生把坡度、坡角问题转化为解直角三角形问题,
从而 会把实际问题转化为数学问题来解决,进一步
提高数学建模能力;
2.通过综合运用勾股定理,直角三角形的两个锐角互
余及锐角三角函数解直角三角形,逐步培养学生分
析问题、解决问题的能力.
教学重点:
将坡度、坡角问题中的数量关系,归结为直角三角形
元素之间的关系,从而利用所学知识解决实际题.
课件说明
l
h
α
i=h:l
正切经常用来描述坡面的坡度.
坡面的铅直高度h和水平长度l 的比叫做坡面的坡度.
i=
h
l
(坡度通常写成h:l 的形式)
记作i .
复习旧知
l
h
α
i=h:l
正切经常用来描述坡面的坡度.
坡面与水平面的夹角叫做坡角(或称倾斜角),
i=
h
l
=tanα
坡度越大,坡角越大,坡面就越陡.
于是有:
记作α .
2.如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的坡度为2: 5 ,则此斜坡的水平距离 m.
A
B
75
C
2: 5=
30: x
2x=150
1.已知坡面的坡度为1:1,则这个坡面的坡角 α为( ).
A.15° B.20° C.30° D. 45°
D
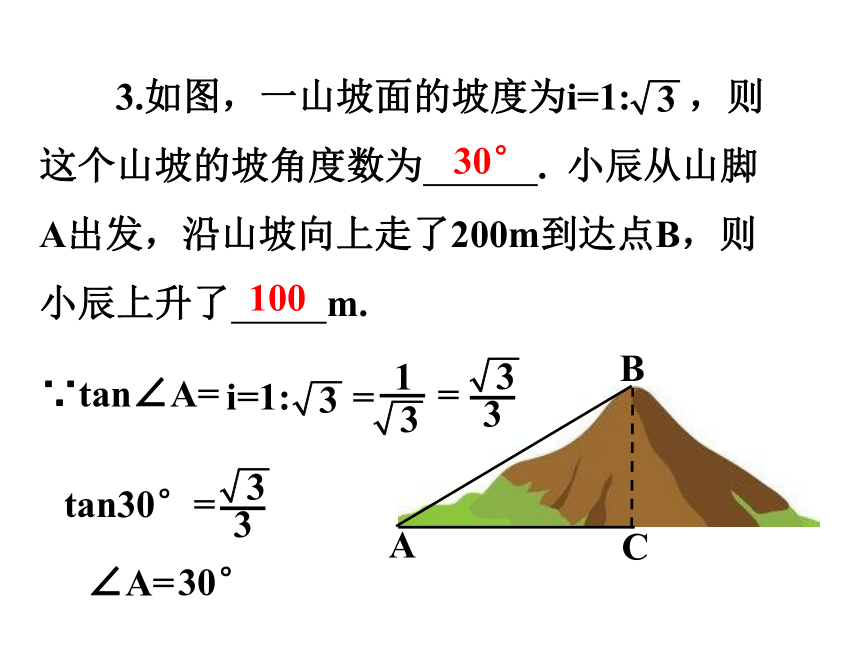
3.如图,一山坡面的坡度为i=1: ,则这个山坡的坡角度数为 . 小辰从山脚A出发,沿山坡向上走了200m到达点B,则小辰上升了 m.
3
A
B
30°
100
C
∵tan∠A=
i=1:
1
=
3
=
3
tan30°=
3
3
3
3
∠A=
30°
4.如图,一名滑雪运动员沿着坡角为34°的斜坡, 从A滑行至B,已知AB=500m,则这名滑雪运动员的高度下降了 m.
(参考数据:sin34°≈0.56,cos34°≈0.83,
tan34°≈0.67)
B
A
C
34°
∵sin34°=
AC
AB
∴AC=500sin34°
≈500×0.56
280
例6.如图,铁路路基的横断面是四边形ABCD,AD∥BC,路基顶宽BC=9.8米,路基高BE=5.8米,斜坡AB的坡度i=1:1.6,斜坡CD的坡度i′=1:2.5.求路基的下底宽AD的值(精确到0.1米)与斜坡的坡角α和β.(精确到1°).
B
A
D
E
C
9.8m
α
β
i′=1:2.5
i=1:1.6
5.8m
例题解析
B
A
D
E
C
9.8m
α
β
i′=1:2.5
i=1:1.6
5.8m
F
过点C作CF⊥AD于F,得
解:
CF=BE,
EF=BC;
∠A=α,
∠D=β.
∵i=1:1.6,
i′=1:2.5,
BE
AE
=
1
1.6
BE=5.8,
∴
CF
DF
=
1
2.5
∴AE=1.6BE
=1.6×5.8
=9.28
DF=2.5CF
=2.5×5.8
=14.5
∴AD=
AE+EF+DF
=9.28+9.8+14.5
≈33.6(m).
B
A
D
E
C
9.8m
α
β
i′=1:2.5
i=1:1.6
5.8m
F
在Rt△ABE中,
∵tanα=
BE
AE
=
i=1:1.6
=
5
8
∴α≈32°;
=0.625,
在Rt△DCF中,
∵tanβ=
CF
DF
=
i′=1:2.5
=
2
5
∴β≈22°.
=0.4,
答:路基的下底宽为33.6m,
斜坡的坡角分别为32°和22°.
1.如图,水库大坝的横断面是四边形ABCD,BC∥AD,坝顶宽为6m,坝高为23m,斜坡AB的坡度i=1:3,斜坡CD的坡度i′=1:2.5.求:
(1)斜坡AB的坡角α的值.(精确到1°).
(2)坝底宽AD和斜坡AB的值(精确到0.1m)
B
A
D
E
C
6m
α
β
i′=1:2.5
i=1:3
23m
练习巩固
B
A
D
E
C
6m
α
β
i′=1:2.5
i=1:3
∵tanα=
i=1:3
1
3
∴α=18°;
≈0.3333,
解:(1)
=
B
A
D
E
C
6m
α
i′=1:2.5
i=1:3
23m
F
过点C作CF⊥AD于F,得
CF=BE,
EF=BC;
∵i=1:3,
i′=1:2.5,
BE
AE
=
1
3
BE=23,
∴
CF
DF
=
1
2.5
∴AE=3BE
=3×23
=69
DF=2.5CF
=2.5×23
=57.5
∴AD=
AE+EF+DF
=69+6+57.5
=132.5(m).
(2)
B
A
D
E
C
6m
α
β
i′=1:2.5
i=1:3
23m
∵BE=23,
AE=3BE=69,
∴AB2=
AE2+BE2
=692+232
∴AB=
10
23
=232 (32+1)
≈72.7(m).
B
A
D
E
C
6m
α
β
i′=1:2.5
i=1:3
23m
在Rt△ABE中,∠α=18°,
∵sinα=
BE
AB
=
0.31
23
∴AB=
sin18°
BE
≈72.7(m).
2.如图,燕尾槽的横断面是四边形ABCD,AD∥BC,其中∠B=∠C=55°,外口宽AD=180mm,燕尾槽的深度AE=70mm.求它的里口宽BC的值 .(精确到1mm).
E
D
C
B
A
E
D
C
B
A
过点D作DF⊥BC于F.
解:
F
∵ AD∥BC,
AE⊥BC
∴AE=DF,
∵ ∠B=∠C=55°,
∴△ABE≌△DFC.
∴BE=CF.
AD=EF.
在Rt△ABE中,
tan∠B=
AE
BE
∴BE=
AE
tan∠B
=
70
tan55°
=
70
1.43
≈49(mm).
∴BC=
BE+EF+CF
=49+180+49
=278(mm).
答:里口宽BC的值为278mm .
对于坡度、坡角问题,解题的关键是将坡度转化为线段的比,并寻找或构造合适的直角三角形.
课堂小结
1.如图,某山坡的坡面AB=200m,坡角∠BAC=30°,则该山坡的高BC为 m.
A
B
C
30°
巩固提高
100
2.如图,斜坡AB的坡度i=1:3,该斜坡的水平距离AC=6m,则斜坡AB的长为 m.
A
B
C
10
2
i=1:3
6
2
3.如图,某村准备在坡度为1:2的山坡上栽树,要求相邻两棵树之间的水平距离AC为4m,则这两棵树在坡面上的距离AB为 m.
A
B
C
4m
5
2
4.如图,小林从点A出发,沿着坡角为 α的斜坡向上走了650m到达点B,且sinα= .然后又沿着坡度i=1:3的斜坡向上走了500m到达点C.
(1)小林从点A到达点B的高度是 米;
(2)小林从点A到达点C上升的高度CD
是 米.
A
B
C
D
E
α
i=1:3
4
13
200
F
10 )
50
( 200+
今天作业
课本P131页第5题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
