23.2 解直角三角形及其应用(5) 课件(共25张PPT)
文档属性
| 名称 | 23.2 解直角三角形及其应用(5) 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-06 10:53:15 | ||
图片预览



文档简介
(共25张PPT)
沪科版 九年级上册
23.2 解直角三角形及其应用 (5)
方向角问题
教学目标:
1.使学生把方向角问题转化为解直角三角形问题,从
而会把实际问题转化为数学问题来解决,进一步提
高数学建模能力;
2.通过综合运用勾股定理,直角三角形的两个锐角互
余及锐角三角函数解直角三角形,逐步培养学生分
析问题、解决问题的能力.
教学重点:
将方向角问题中的数量关系,归结为直角三角形
元素之间的关系,从而利用所学知识解决实际题.
课件说明
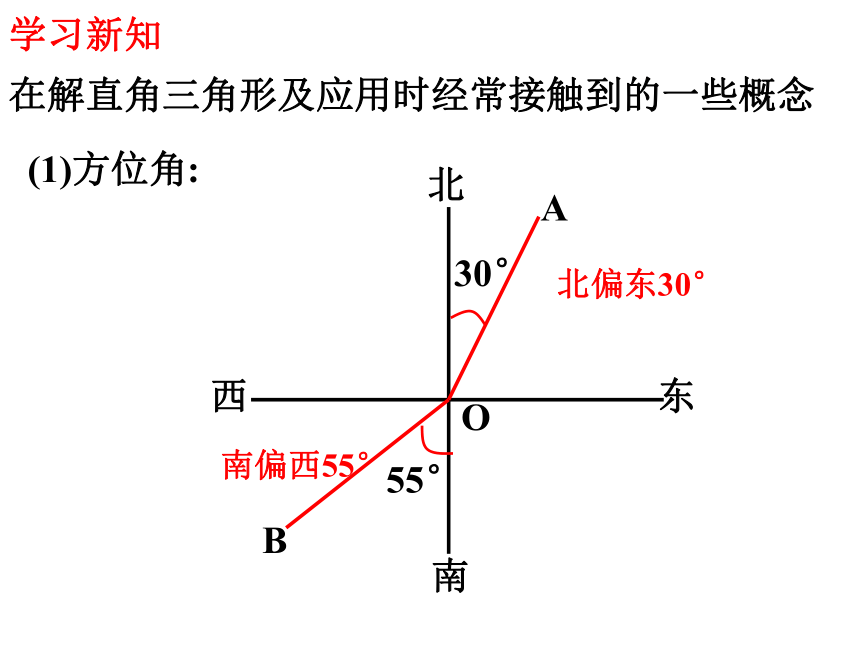
在解直角三角形及应用时经常接触到的一些概念
(1)方位角:
O
东
西
北
南
30°
55°
北偏东30°
南偏西55°
A
B
学习新知
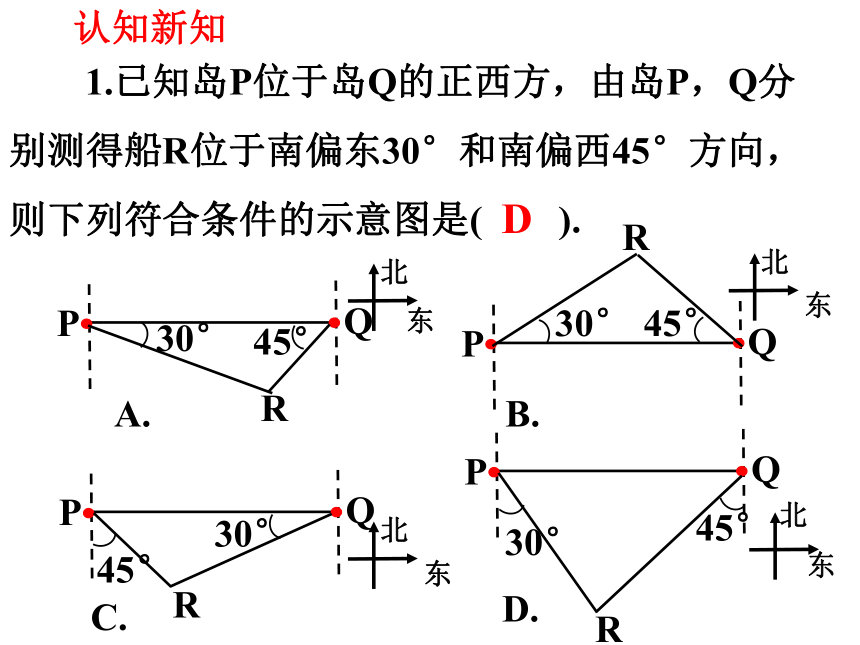
1.已知岛P位于岛Q的正西方,由岛P,Q分 别测得船R位于南偏东30°和南偏西45°方向,则下列符合条件的示意图是( ).
认知新知
P
R
Q
P
R
Q
东
北
东
北
45°
30°
30°
45°
P
R
Q
东
北
45°
东
北
P
R
Q
A.
30°
30°
45°
B.
C.
D.
D
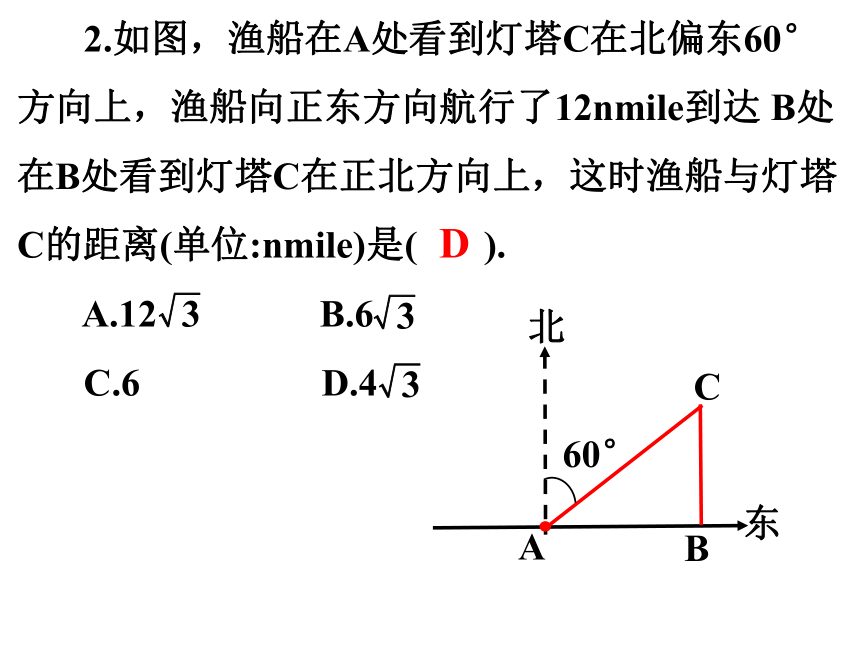
2.如图,渔船在A处看到灯塔C在北偏东60°方向上,渔船向正东方向航行了12nmile到达 B处在B处看到灯塔C在正北方向上,这时渔船与灯塔C的距离(单位:nmile)是( ).
A.12 B.6
C.6 D.4
3
3
3
A
东
北
B
C
60°
D
3.如图,学校在小明家北偏西30°方向,且距小明家6m,那么学校所在位置A点的坐标是( ).
A.(3,3 )
B.(-3 ,3)
C.(-3,3 )
D.(3, -3 )
3
3
3
3
A
x
y
O
30°
东
北
C
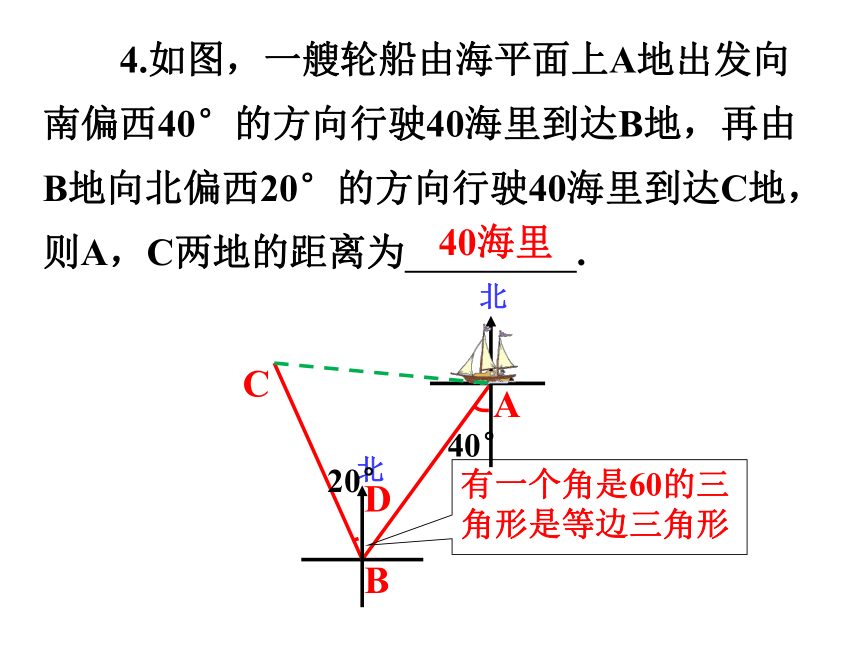
4.如图,一艘轮船由海平面上A地出发向南偏西40°的方向行驶40海里到达B地,再由B地向北偏西20°的方向行驶40海里到达C地,则A,C两地的距离为 .
北
A
北
B
C
40海里
D
有一个角是60的三角形是等边三角形
40°
20°
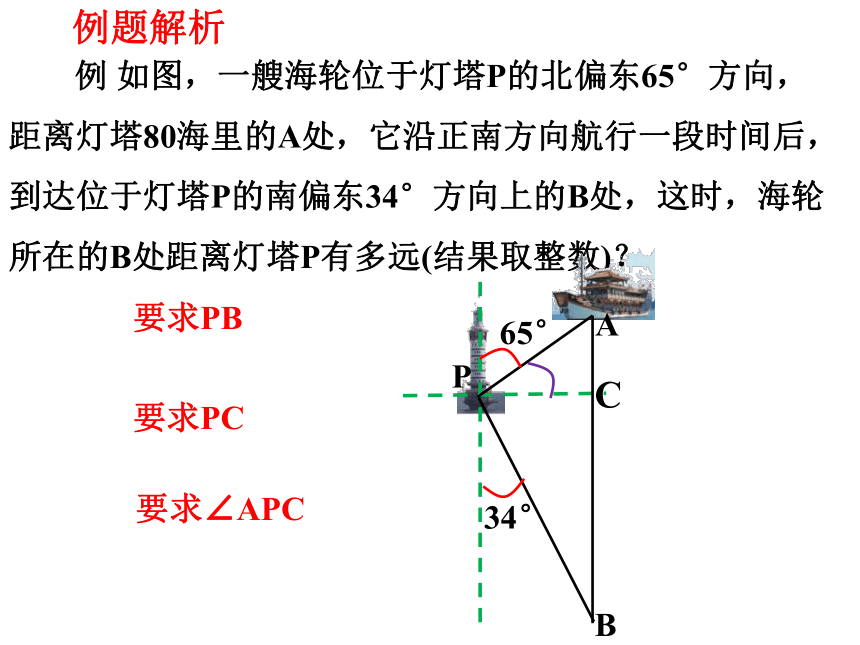
例 如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(结果取整数)?
65°
34°
P
B
A
C
要求PB
要求PC
要求∠APC
例题解析
65°
34°
P
B
A
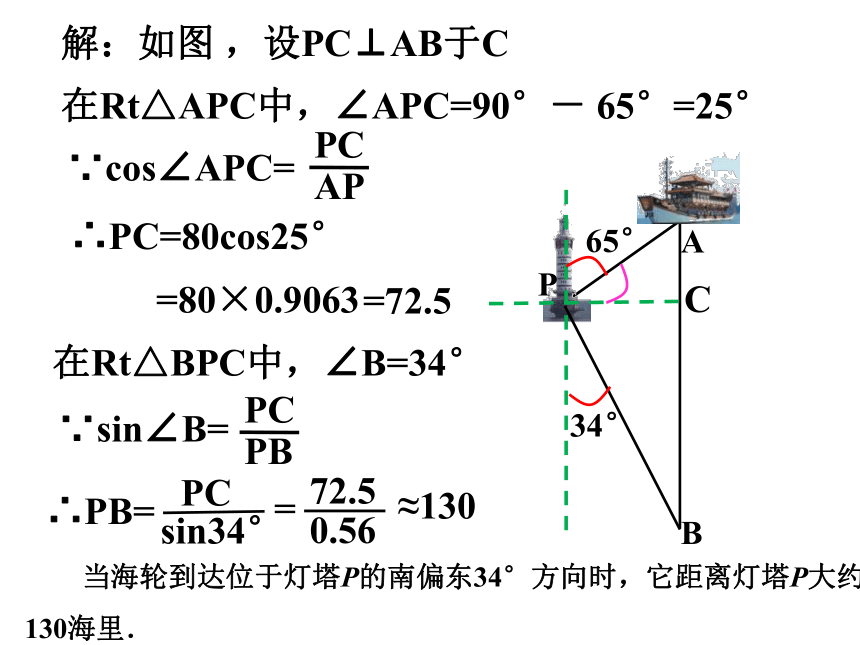
解:如图 ,设PC⊥AB于C
在Rt△APC中,∠APC=90°- 65°=25°
∵cos∠APC=
PC
AP
∴PC=80cos25°
=80×0.9063
在Rt△BPC中,∠B=34°
∵sin∠B=
PC
PB
=
0.56
72.5
≈130
∴PB=
sin34°
PC
当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约130海里.
C
=72.5
例5.一船以20 n mile/h的速度向东航行,在A处测得灯塔C在北偏东60°方向上,继续航行1h到达B处,再测得灯塔C在北偏东30°方向上. 已知灯塔C四周10 n mile内有暗礁,问这船继续向东航行是否安全?
C
B
D
20
60°
30°
向东航行是否安全?
灯塔C到航线的距离
是否大于10
A
例题解析
A
C
B
D
解:由点C作AB的垂线
交AB的延长线于点D,垂足为D,
由题意图示可知∠CAD=30° ,
在Rt△BCD中,
∴BD=10.
> 10,
∴这船继续向东航行是安全的.
∴CD=10
60°
∠CBD=60°.
∵tan∠CBD=
∴CD=BD tan60°
在Rt△ACD中,
∵tan∠CAD=
=
3
BD.
∴tan30°=
20+BD
CD
3
3
∴
=
20+BD
3
BD
3
,
CD
AD
,
.
CD
BD
,
30°
一船向东航行,上午9:00到达灯塔C的西南60n mile的点A处,上午10:00到达灯塔C的正南的点B处.
(1)画出示意图.
(2)求这船的航行速度.
(结果保留根号).
C
A
B
解:
(1)
练习巩固
一船向东航行,上午9:00到达灯塔C的西南60n mile的点A处,上午10:00到达灯塔C的正南的点B处. (2)求这船的航行速度(结果保留根号).
C
A
B
(2)
在Rt△BPC中,∠A=45°,AC=60
∵cos∠A=
AB
AC
∴AB=ACcos45°
=60×
2
2
30
2
=30
2
÷1
=30
2
(n mile/h)
答:这船的航行速度为
30
2
n mile/h.
对于方向角问题,首先要清楚方向角的表示方法,然后将实际问题抽象成数学问题,并将问题转化到直角三角形中求解.解题时要充分利用表示南北和东西的方向线作辅助线或寻找角度之间的关系.
课堂小结
1. 如图 ,甲从点 A 出发向北偏东 60°方向走到点B,乙从点A出发向南偏西 20°方向走到点C,则∠BAC的度数是( ).
A.80° B. 100°
C.120° D.140°
巩固提高
A
东
北
B
C
60°
20°
D
2.如图,一艘海轮位于灯塔P的北偏东55°方向距离灯塔2nmile的点A处.若海轮沿正南方向航行到灯塔的正东方向,则海轮航行的距离AB为( ).
A.2 n mile
B. 2cos 55°n mile
C. 2sin 55°n mile
D. 2tan 55°n mile
A
东
北
B
P
55°
B
3.如图,一艘船向东航行,上午8时到达A处,此时测得灯塔B在船的北偏东 30°方向,且距离船48nmile.上午11时船到达C处,此时测得灯塔 B在船的正北方向,则这艘船航行的速度是( ).
A.24 n mile/h
B. 8 n mile/h
C.24 n mile/h
D. 8 n mile/h
A
东
北
B
C
3
3
D
30°
4.如图,一艘海轮位于灯塔P的南偏东45°方向,距离灯塔60nmile的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东30°方向上的B处,这时,B处与灯塔P的距离为( ).
A.60 n mile
B. 60 n mile
C.30 n mile
D. 30 n
3
2
3
2
A
东
北
B
P
30°
45°
B
5.如图,某海防哨所O发现在它的北偏西30°方向,距离为400m的A处有一艘船,该船向正东方向航行,经过2min到达哨所东北方向的B处,则该船的航速为 m/min. (结果保留根号)
A
东
北
B
O
30°
45°
3)
100
(100+
6.如图,轮船在A处观测灯塔C位于北偏东70°方向上,轮船从A处以30nmile/h的速度沿南偏东50°方向匀速航行,1h后到达码头B处,此时观测灯塔C位于北偏东25方向上,则灯塔C与码头B之间的距离是 nmile(结果保留根号).
东
北
A
B
C
70°
50°
25°
6
15
D
7.如图,渔船由西向东航行,到达A处时,测得小岛C位于它的北偏东53°方向,再航行3km后达到B处,测得小岛C位于它的北偏东45°方向.小岛C的周围8km内有暗礁,若渔船不改变航向继续向东航行,请你通过计算说明渔船有无触礁的危险(参考数据:sin 53°≈ ,cos 53≈ ,tan 53°≈ .)
C
A
东
北
B
45°
53°
3
4
5
4
5
3
答:渔船没有触礁的危险.
C
A
东
北
B
45°
53°
D
解得x=9
>8
解:过点C作CD⊥AB于点D,
则∠ ACD=53°,
∠BCD=∠CBD= 45°.
∴ BD=CD.
设CD=xkm,
则BD=xkm,
在Rt△ACD中,tan∠ACD= ·
∴ tan 58°=
AD=AB+BD
=
CD
AD
x
3+x
3
4
=(3+x)m.
∴ 3(3+x)=4x
今天作业
课本P132页第7题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级上册
23.2 解直角三角形及其应用 (5)
方向角问题
教学目标:
1.使学生把方向角问题转化为解直角三角形问题,从
而会把实际问题转化为数学问题来解决,进一步提
高数学建模能力;
2.通过综合运用勾股定理,直角三角形的两个锐角互
余及锐角三角函数解直角三角形,逐步培养学生分
析问题、解决问题的能力.
教学重点:
将方向角问题中的数量关系,归结为直角三角形
元素之间的关系,从而利用所学知识解决实际题.
课件说明
在解直角三角形及应用时经常接触到的一些概念
(1)方位角:
O
东
西
北
南
30°
55°
北偏东30°
南偏西55°
A
B
学习新知
1.已知岛P位于岛Q的正西方,由岛P,Q分 别测得船R位于南偏东30°和南偏西45°方向,则下列符合条件的示意图是( ).
认知新知
P
R
Q
P
R
Q
东
北
东
北
45°
30°
30°
45°
P
R
Q
东
北
45°
东
北
P
R
Q
A.
30°
30°
45°
B.
C.
D.
D
2.如图,渔船在A处看到灯塔C在北偏东60°方向上,渔船向正东方向航行了12nmile到达 B处在B处看到灯塔C在正北方向上,这时渔船与灯塔C的距离(单位:nmile)是( ).
A.12 B.6
C.6 D.4
3
3
3
A
东
北
B
C
60°
D
3.如图,学校在小明家北偏西30°方向,且距小明家6m,那么学校所在位置A点的坐标是( ).
A.(3,3 )
B.(-3 ,3)
C.(-3,3 )
D.(3, -3 )
3
3
3
3
A
x
y
O
30°
东
北
C
4.如图,一艘轮船由海平面上A地出发向南偏西40°的方向行驶40海里到达B地,再由B地向北偏西20°的方向行驶40海里到达C地,则A,C两地的距离为 .
北
A
北
B
C
40海里
D
有一个角是60的三角形是等边三角形
40°
20°
例 如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(结果取整数)?
65°
34°
P
B
A
C
要求PB
要求PC
要求∠APC
例题解析
65°
34°
P
B
A
解:如图 ,设PC⊥AB于C
在Rt△APC中,∠APC=90°- 65°=25°
∵cos∠APC=
PC
AP
∴PC=80cos25°
=80×0.9063
在Rt△BPC中,∠B=34°
∵sin∠B=
PC
PB
=
0.56
72.5
≈130
∴PB=
sin34°
PC
当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约130海里.
C
=72.5
例5.一船以20 n mile/h的速度向东航行,在A处测得灯塔C在北偏东60°方向上,继续航行1h到达B处,再测得灯塔C在北偏东30°方向上. 已知灯塔C四周10 n mile内有暗礁,问这船继续向东航行是否安全?
C
B
D
20
60°
30°
向东航行是否安全?
灯塔C到航线的距离
是否大于10
A
例题解析
A
C
B
D
解:由点C作AB的垂线
交AB的延长线于点D,垂足为D,
由题意图示可知∠CAD=30° ,
在Rt△BCD中,
∴BD=10.
> 10,
∴这船继续向东航行是安全的.
∴CD=10
60°
∠CBD=60°.
∵tan∠CBD=
∴CD=BD tan60°
在Rt△ACD中,
∵tan∠CAD=
=
3
BD.
∴tan30°=
20+BD
CD
3
3
∴
=
20+BD
3
BD
3
,
CD
AD
,
.
CD
BD
,
30°
一船向东航行,上午9:00到达灯塔C的西南60n mile的点A处,上午10:00到达灯塔C的正南的点B处.
(1)画出示意图.
(2)求这船的航行速度.
(结果保留根号).
C
A
B
解:
(1)
练习巩固
一船向东航行,上午9:00到达灯塔C的西南60n mile的点A处,上午10:00到达灯塔C的正南的点B处. (2)求这船的航行速度(结果保留根号).
C
A
B
(2)
在Rt△BPC中,∠A=45°,AC=60
∵cos∠A=
AB
AC
∴AB=ACcos45°
=60×
2
2
30
2
=30
2
÷1
=30
2
(n mile/h)
答:这船的航行速度为
30
2
n mile/h.
对于方向角问题,首先要清楚方向角的表示方法,然后将实际问题抽象成数学问题,并将问题转化到直角三角形中求解.解题时要充分利用表示南北和东西的方向线作辅助线或寻找角度之间的关系.
课堂小结
1. 如图 ,甲从点 A 出发向北偏东 60°方向走到点B,乙从点A出发向南偏西 20°方向走到点C,则∠BAC的度数是( ).
A.80° B. 100°
C.120° D.140°
巩固提高
A
东
北
B
C
60°
20°
D
2.如图,一艘海轮位于灯塔P的北偏东55°方向距离灯塔2nmile的点A处.若海轮沿正南方向航行到灯塔的正东方向,则海轮航行的距离AB为( ).
A.2 n mile
B. 2cos 55°n mile
C. 2sin 55°n mile
D. 2tan 55°n mile
A
东
北
B
P
55°
B
3.如图,一艘船向东航行,上午8时到达A处,此时测得灯塔B在船的北偏东 30°方向,且距离船48nmile.上午11时船到达C处,此时测得灯塔 B在船的正北方向,则这艘船航行的速度是( ).
A.24 n mile/h
B. 8 n mile/h
C.24 n mile/h
D. 8 n mile/h
A
东
北
B
C
3
3
D
30°
4.如图,一艘海轮位于灯塔P的南偏东45°方向,距离灯塔60nmile的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东30°方向上的B处,这时,B处与灯塔P的距离为( ).
A.60 n mile
B. 60 n mile
C.30 n mile
D. 30 n
3
2
3
2
A
东
北
B
P
30°
45°
B
5.如图,某海防哨所O发现在它的北偏西30°方向,距离为400m的A处有一艘船,该船向正东方向航行,经过2min到达哨所东北方向的B处,则该船的航速为 m/min. (结果保留根号)
A
东
北
B
O
30°
45°
3)
100
(100+
6.如图,轮船在A处观测灯塔C位于北偏东70°方向上,轮船从A处以30nmile/h的速度沿南偏东50°方向匀速航行,1h后到达码头B处,此时观测灯塔C位于北偏东25方向上,则灯塔C与码头B之间的距离是 nmile(结果保留根号).
东
北
A
B
C
70°
50°
25°
6
15
D
7.如图,渔船由西向东航行,到达A处时,测得小岛C位于它的北偏东53°方向,再航行3km后达到B处,测得小岛C位于它的北偏东45°方向.小岛C的周围8km内有暗礁,若渔船不改变航向继续向东航行,请你通过计算说明渔船有无触礁的危险(参考数据:sin 53°≈ ,cos 53≈ ,tan 53°≈ .)
C
A
东
北
B
45°
53°
3
4
5
4
5
3
答:渔船没有触礁的危险.
C
A
东
北
B
45°
53°
D
解得x=9
>8
解:过点C作CD⊥AB于点D,
则∠ ACD=53°,
∠BCD=∠CBD= 45°.
∴ BD=CD.
设CD=xkm,
则BD=xkm,
在Rt△ACD中,tan∠ACD= ·
∴ tan 58°=
AD=AB+BD
=
CD
AD
x
3+x
3
4
=(3+x)m.
∴ 3(3+x)=4x
今天作业
课本P132页第7题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
