23.2 解直角三角形及其应用(7) 课件(共25张PPT)
文档属性
| 名称 | 23.2 解直角三角形及其应用(7) 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 969.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-06 11:07:36 | ||
图片预览



文档简介
(共25张PPT)
沪科版 九年级上册
23.2 解直角三角形及其应用 (7)
教学目标:
1.使学生知道直线的斜率的概念,知道斜率是从“数”
的角度刻画平面直角坐标系内一条直线的倾斜程度.
2.两点确定一条直线,知道由两点的坐标就可确定直线
的斜率.
教学重点:
会从“数”的角度刻画平面直角坐标系内一条直线的
倾斜程度.
课件说明
l
h
α
i=h:l
正切经常用来描述坡面的坡度.
坡面的铅直高度h和水平长度l 的比叫做坡面的坡度.
i=
h
l
(坡度通常写成h:l 的形式)
记作i .
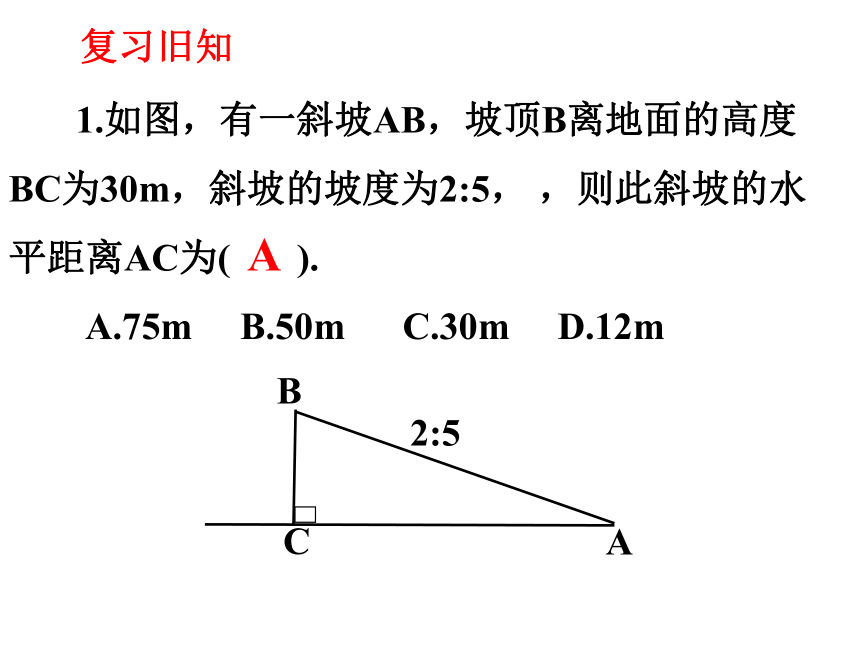
复习旧知
1.如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的坡度为2:5, ,则此斜坡的水平距离AC为( ).
A.75m B.50m C.30m D.12m
A
A
B
C
2:5
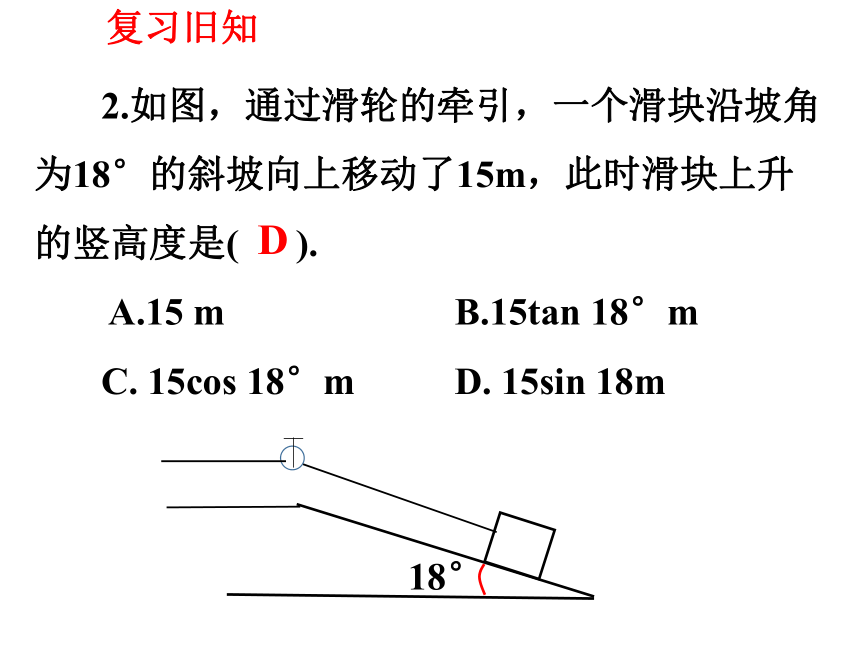
复习旧知
2.如图,通过滑轮的牵引,一个滑块沿坡角为18°的斜坡向上移动了15m,此时滑块上升的竖高度是( ).
A.15 m B.15tan 18°m
C. 15cos 18°m D. 15sin 18m
D
18°
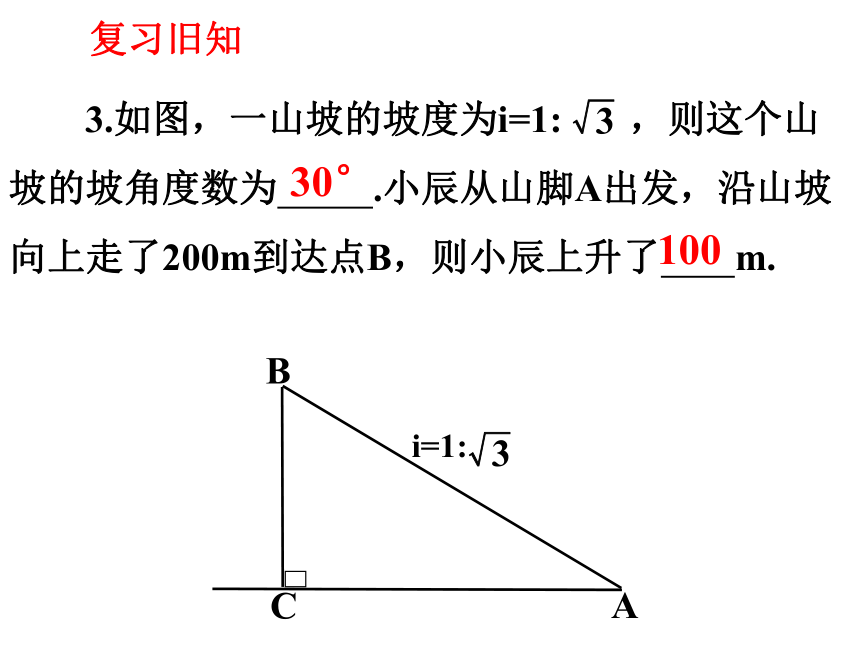
复习旧知
3.如图,一山坡的坡度为i=1: ,则这个山坡的坡角度数为 .小辰从山脚A出发,沿山坡向上走了200m到达点B,则小辰上升了 m.
3
复习旧知
A
B
C
i=1:
3
30°
100
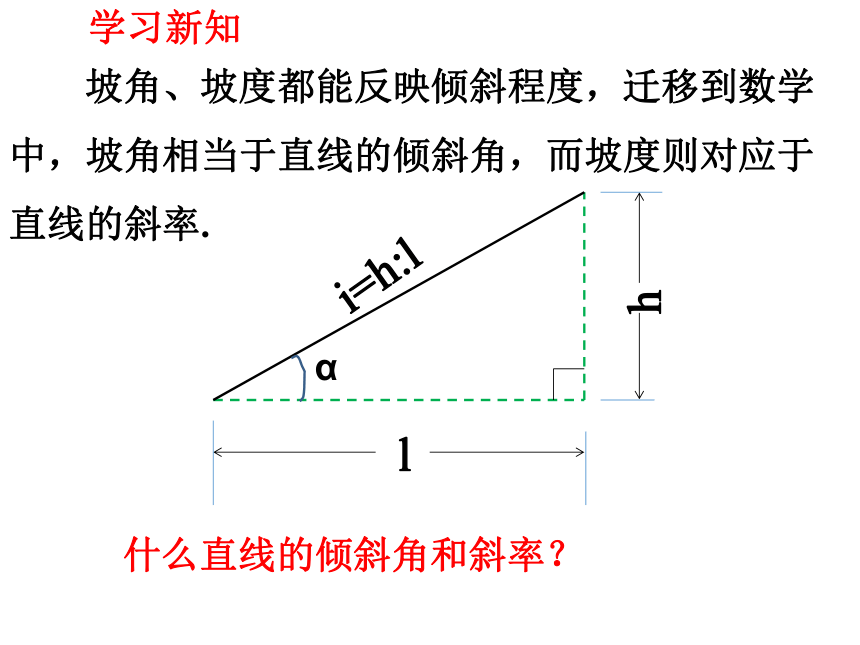
坡角、坡度都能反映倾斜程度,迁移到数学中,坡角相当于直线的倾斜角,而坡度则对应于直线的斜率.
l
h
α
i=h:l
什么直线的倾斜角和斜率?
学习新知
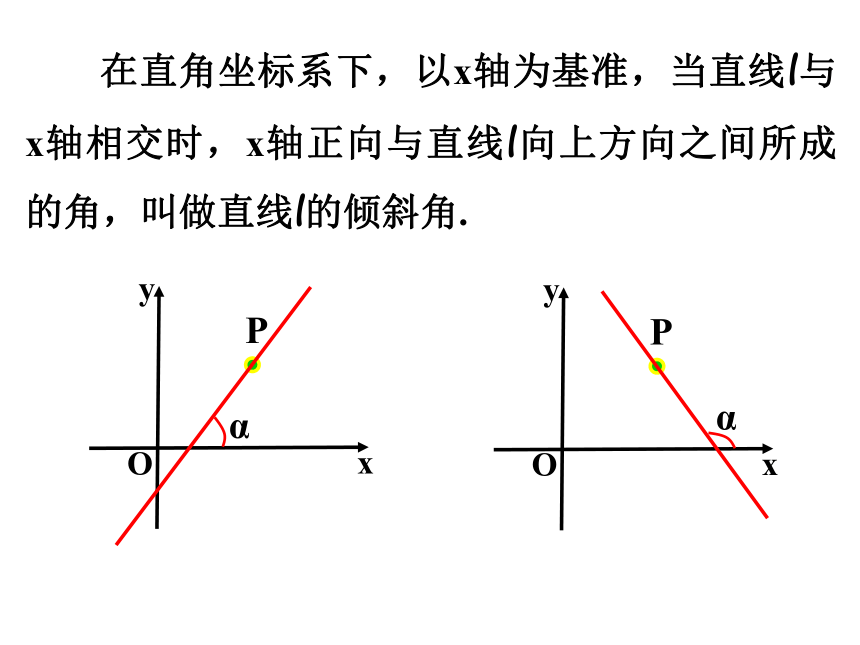
x
y
O
P
x
y
O
P
α
α
在直角坐标系下,以x轴为基准,当直线l与x轴相交时,x轴正向与直线l向上方向之间所成的角,叫做直线l的倾斜角.
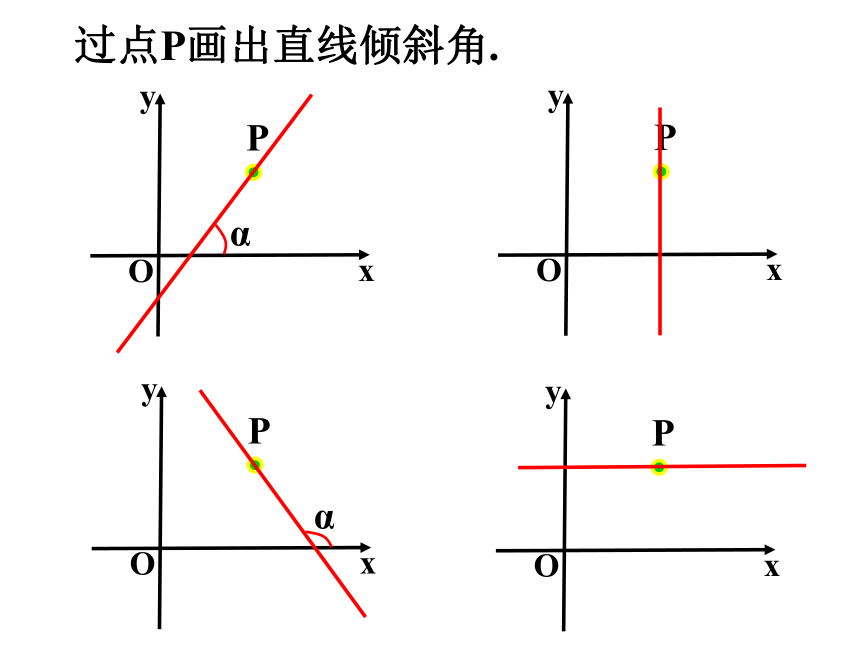
过点P画出直线倾斜角.
x
y
O
P
x
y
O
P
x
y
O
P
x
y
O
P
α
α
过点P画出直线倾斜角.
x
y
O
P
x
y
O
P
α
α
平面直角坐标系中每条直线都有唯一一个确定的倾斜角与它对应.倾斜程度相同的直线,其倾斜角相等,倾斜程度不同的直线,其倾斜角不相等.
x
y
O
P
x
y
O
P
α
α
倾斜角是从“形”的角度刻画平面直角坐标系内一条直线的倾斜程度.
能从“数”的角度刻画平面直角坐标系内一条直线的倾斜程度吗?
直线的斜率: 一条直线的倾斜角α(α≠90°)的正切值叫做这条直线的斜率,斜率常用小写字母k表示,也就是 k = tanα.
x
y
O
P
α
斜率就是从“数”的角度刻画平面直角坐标系内一条直线的倾斜程度.
x
y
O
P
α
斜率是从“数”的角度刻画平面直角坐标系内一条直线的倾斜程度.
两点确定一条直线,可见由两点也就确定了直线的斜率.
x
y
O
α
P1(x1 , y1)
P2(x2 , y2)
Q1
Q2
y=kx+b
如何用P1(x1 ,y1)、P2(x2 ,y2)的坐标来表示直线斜率k?
在平面直角坐标系中,已知直线上两点P1,P2,
例7 已知:在直线上y=kx+b有任意两点
P1(x1 , y1), P2(x2 , y2) ,这条直线向上方向与x轴正方向所夹的锐角为α.
求证:
tanα=
=k
y2 - y1
x2 -x1
x
y
O
α
P1(x1 , y1)
P2(x2 , y2)
y=kx+b
求证:
tanα=
=k
y2 - y1
x2 -x1
α
x
y
O
P1(x1 , y1)
P2(x2 , y2)
R
Q1
Q2
α
y=kx+b
设x1<x2,
证明:
则y1<y2.
∵α是锐角,
∴tanα>0,
过点P1 , P2作x轴的垂线,
垂足分别为Q1 , Q2,
再过点P1 作x轴的平行线P1R
交P2Q2于点R,得
∠P2P1R=α,
在Rt△P2P1R中,
tanα=
RP2
RP1
=
|x2-x1|
|y2-y1|
=
x2-x1
y2-y1
tan∠P2P1R=
α
x
y
O
P1(x1 , y1)
P2(x2 , y2)
R
Q1
Q2
α
y=kx+b
在Rt△P2P1R中,
tanα=
RP2
RP1
=
|x2-x1|
|y2-y1|
=
x2-x1
y2-y1
∵P1, P2在直线y=kx+b上,
∴y1=kx1+b,
y2=kx2+b.
∴ y2-y1=
kx2-kx1
=k(x2-x1)
∴k=
x2-x1
y2-y1
∴tanα=
x2-x1
y2-y1
=k.
求直线y= x-5的向上方向与x轴正方向所夹的锐角.
3
x
y
O
y= x-5
3
解:
∵tanα=k,
k=
3
∴ tanα=
3
∵tan60°=
3
∴ α =60°.
设所求的锐角为α.
例题解析
1. 已知一直线经过A(2 , 2), B(4 , 6)两点,求这条直线解析式.
解:
∴所求的直线解析式为y=2x-2.
则
∴
设所求的直线解析式为y=kx+b.
2k+b=2
4k+b=6
b=-2
k=2
练习巩固
1. 已知一直线经过A(2 , 2), B(4 , 6)两点,求这条直线解析式.
解:
∴所求的直线解析式为y=2x-2.
则
k=
4-2
6-2
=2
∵ y=2x+b 经过A(2 , 2),
∴ 2=2×2+b.
∴ b=-2.
设所求的直线解析式为y=kx+b.
2.过点M(-2,m)、N(m,4)的直线的斜率等于1,则m的值为 .
解:
x2-x1
y2-y1
∵
∴
=1,
m+2
4-m
=1
∴m+2=4-m,
∴2m=2,
∴m=1.
1
3. 已知一直线经过A(2 , 0), B(5 , 3)两点,求这条直线的斜率和倾斜角.
解:
设所求的斜率为k,倾斜角为α.
则
k=
5-2
3-0
=1
∵tanα=1,
0°<α<90°,
∴ α=45°.
∴这条直线的斜率为1,倾斜角为45°.
今天作业
课本P132页第6题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级上册
23.2 解直角三角形及其应用 (7)
教学目标:
1.使学生知道直线的斜率的概念,知道斜率是从“数”
的角度刻画平面直角坐标系内一条直线的倾斜程度.
2.两点确定一条直线,知道由两点的坐标就可确定直线
的斜率.
教学重点:
会从“数”的角度刻画平面直角坐标系内一条直线的
倾斜程度.
课件说明
l
h
α
i=h:l
正切经常用来描述坡面的坡度.
坡面的铅直高度h和水平长度l 的比叫做坡面的坡度.
i=
h
l
(坡度通常写成h:l 的形式)
记作i .
复习旧知
1.如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的坡度为2:5, ,则此斜坡的水平距离AC为( ).
A.75m B.50m C.30m D.12m
A
A
B
C
2:5
复习旧知
2.如图,通过滑轮的牵引,一个滑块沿坡角为18°的斜坡向上移动了15m,此时滑块上升的竖高度是( ).
A.15 m B.15tan 18°m
C. 15cos 18°m D. 15sin 18m
D
18°
复习旧知
3.如图,一山坡的坡度为i=1: ,则这个山坡的坡角度数为 .小辰从山脚A出发,沿山坡向上走了200m到达点B,则小辰上升了 m.
3
复习旧知
A
B
C
i=1:
3
30°
100
坡角、坡度都能反映倾斜程度,迁移到数学中,坡角相当于直线的倾斜角,而坡度则对应于直线的斜率.
l
h
α
i=h:l
什么直线的倾斜角和斜率?
学习新知
x
y
O
P
x
y
O
P
α
α
在直角坐标系下,以x轴为基准,当直线l与x轴相交时,x轴正向与直线l向上方向之间所成的角,叫做直线l的倾斜角.
过点P画出直线倾斜角.
x
y
O
P
x
y
O
P
x
y
O
P
x
y
O
P
α
α
过点P画出直线倾斜角.
x
y
O
P
x
y
O
P
α
α
平面直角坐标系中每条直线都有唯一一个确定的倾斜角与它对应.倾斜程度相同的直线,其倾斜角相等,倾斜程度不同的直线,其倾斜角不相等.
x
y
O
P
x
y
O
P
α
α
倾斜角是从“形”的角度刻画平面直角坐标系内一条直线的倾斜程度.
能从“数”的角度刻画平面直角坐标系内一条直线的倾斜程度吗?
直线的斜率: 一条直线的倾斜角α(α≠90°)的正切值叫做这条直线的斜率,斜率常用小写字母k表示,也就是 k = tanα.
x
y
O
P
α
斜率就是从“数”的角度刻画平面直角坐标系内一条直线的倾斜程度.
x
y
O
P
α
斜率是从“数”的角度刻画平面直角坐标系内一条直线的倾斜程度.
两点确定一条直线,可见由两点也就确定了直线的斜率.
x
y
O
α
P1(x1 , y1)
P2(x2 , y2)
Q1
Q2
y=kx+b
如何用P1(x1 ,y1)、P2(x2 ,y2)的坐标来表示直线斜率k?
在平面直角坐标系中,已知直线上两点P1,P2,
例7 已知:在直线上y=kx+b有任意两点
P1(x1 , y1), P2(x2 , y2) ,这条直线向上方向与x轴正方向所夹的锐角为α.
求证:
tanα=
=k
y2 - y1
x2 -x1
x
y
O
α
P1(x1 , y1)
P2(x2 , y2)
y=kx+b
求证:
tanα=
=k
y2 - y1
x2 -x1
α
x
y
O
P1(x1 , y1)
P2(x2 , y2)
R
Q1
Q2
α
y=kx+b
设x1<x2,
证明:
则y1<y2.
∵α是锐角,
∴tanα>0,
过点P1 , P2作x轴的垂线,
垂足分别为Q1 , Q2,
再过点P1 作x轴的平行线P1R
交P2Q2于点R,得
∠P2P1R=α,
在Rt△P2P1R中,
tanα=
RP2
RP1
=
|x2-x1|
|y2-y1|
=
x2-x1
y2-y1
tan∠P2P1R=
α
x
y
O
P1(x1 , y1)
P2(x2 , y2)
R
Q1
Q2
α
y=kx+b
在Rt△P2P1R中,
tanα=
RP2
RP1
=
|x2-x1|
|y2-y1|
=
x2-x1
y2-y1
∵P1, P2在直线y=kx+b上,
∴y1=kx1+b,
y2=kx2+b.
∴ y2-y1=
kx2-kx1
=k(x2-x1)
∴k=
x2-x1
y2-y1
∴tanα=
x2-x1
y2-y1
=k.
求直线y= x-5的向上方向与x轴正方向所夹的锐角.
3
x
y
O
y= x-5
3
解:
∵tanα=k,
k=
3
∴ tanα=
3
∵tan60°=
3
∴ α =60°.
设所求的锐角为α.
例题解析
1. 已知一直线经过A(2 , 2), B(4 , 6)两点,求这条直线解析式.
解:
∴所求的直线解析式为y=2x-2.
则
∴
设所求的直线解析式为y=kx+b.
2k+b=2
4k+b=6
b=-2
k=2
练习巩固
1. 已知一直线经过A(2 , 2), B(4 , 6)两点,求这条直线解析式.
解:
∴所求的直线解析式为y=2x-2.
则
k=
4-2
6-2
=2
∵ y=2x+b 经过A(2 , 2),
∴ 2=2×2+b.
∴ b=-2.
设所求的直线解析式为y=kx+b.
2.过点M(-2,m)、N(m,4)的直线的斜率等于1,则m的值为 .
解:
x2-x1
y2-y1
∵
∴
=1,
m+2
4-m
=1
∴m+2=4-m,
∴2m=2,
∴m=1.
1
3. 已知一直线经过A(2 , 0), B(5 , 3)两点,求这条直线的斜率和倾斜角.
解:
设所求的斜率为k,倾斜角为α.
则
k=
5-2
3-0
=1
∵tanα=1,
0°<α<90°,
∴ α=45°.
∴这条直线的斜率为1,倾斜角为45°.
今天作业
课本P132页第6题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
