26.2用函数观点看一元二次方程[下学期]
文档属性
| 名称 | 26.2用函数观点看一元二次方程[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 73.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-29 17:41:00 | ||
图片预览






文档简介
课件16张PPT。26.2 用函数观点看一 元二次方程问题以40m/s的速度将小球沿与地面成30°角的方向击出时,
球的飞行路线将是一条抛物线.如果不考虑空气阻力,球
的飞行高度h(单位:m)与飞行时间t (单位:s)之间具有关系.考虑以下问题:
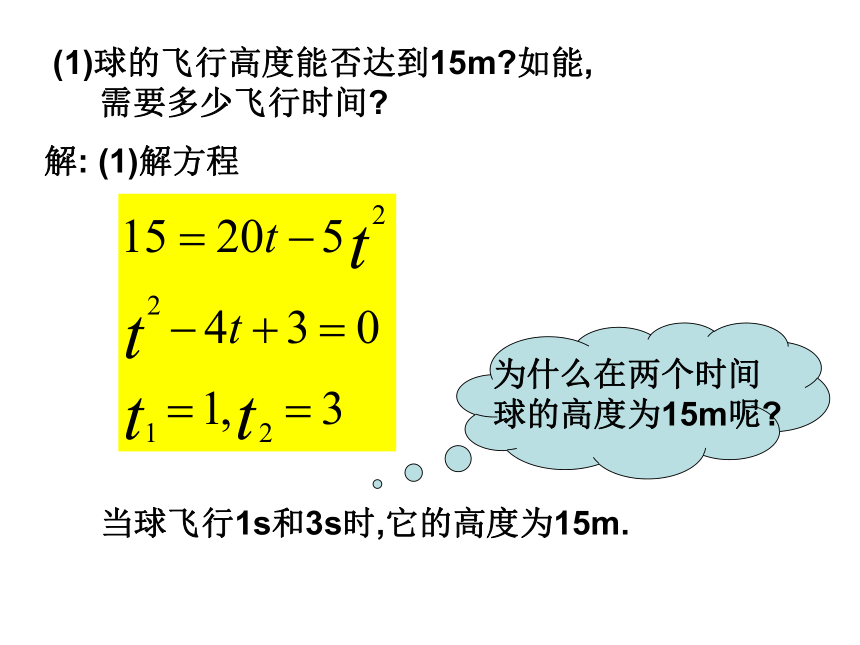
(1)球的飞行高度能否达到15m?如能,
需要多少飞行时间?
(2)球的飞行高度能否达到20m?如能,
需要多少飞行时间?
(3) 球的飞行高度能否达到20.5m?为什么?
(4)球从飞出到落地要用多少时间?(1)球的飞行高度能否达到15m?如能,
需要多少飞行时间?解: (1)解方程当球飞行1s和3s时,它的高度为15m.为什么在两个时间
球的高度为15m呢?(2)球的飞行高度能否达到20m?如能,
需要多少飞行时间?解: (2)解方程当球飞行2s时,它的高度为20m.为什么只在一个时间
内球的高度为20m呢?(3) 球的飞行高度能否达到20.5m?为什么?解: (3)解方程解: (4)解方程(4)球从飞出到落地要用多少时间?当球飞行0s和4s时,它的高度为0m,
即0s时球从地面飞出, 4s时球落回地面.为什么在两个时间
球的高度为0m呢?归纳:观察解:归纳:(1) 没有公共点 没有实数根(2)有一个公共点 有两个相等的实数根(3)有两个公共点 有两个不等的实数根例解:方法: (1)先作出图象;
(2)写出交点的坐标;
(3)得出方程的解.练习CA6.某建筑物的窗户如图所示,它的上半部是半圆,
下半部是矩形,制造窗框的材料长(图中所有黑线
的长度和)为10米.当x等于多少米时,窗户的透光
面积最大? 最大面积是多少?
球的飞行路线将是一条抛物线.如果不考虑空气阻力,球
的飞行高度h(单位:m)与飞行时间t (单位:s)之间具有关系.考虑以下问题:
(1)球的飞行高度能否达到15m?如能,
需要多少飞行时间?
(2)球的飞行高度能否达到20m?如能,
需要多少飞行时间?
(3) 球的飞行高度能否达到20.5m?为什么?
(4)球从飞出到落地要用多少时间?(1)球的飞行高度能否达到15m?如能,
需要多少飞行时间?解: (1)解方程当球飞行1s和3s时,它的高度为15m.为什么在两个时间
球的高度为15m呢?(2)球的飞行高度能否达到20m?如能,
需要多少飞行时间?解: (2)解方程当球飞行2s时,它的高度为20m.为什么只在一个时间
内球的高度为20m呢?(3) 球的飞行高度能否达到20.5m?为什么?解: (3)解方程解: (4)解方程(4)球从飞出到落地要用多少时间?当球飞行0s和4s时,它的高度为0m,
即0s时球从地面飞出, 4s时球落回地面.为什么在两个时间
球的高度为0m呢?归纳:观察解:归纳:(1) 没有公共点 没有实数根(2)有一个公共点 有两个相等的实数根(3)有两个公共点 有两个不等的实数根例解:方法: (1)先作出图象;
(2)写出交点的坐标;
(3)得出方程的解.练习CA6.某建筑物的窗户如图所示,它的上半部是半圆,
下半部是矩形,制造窗框的材料长(图中所有黑线
的长度和)为10米.当x等于多少米时,窗户的透光
面积最大? 最大面积是多少?
同课章节目录
