一元二次方程根的分布[上学期]
文档属性
| 名称 | 一元二次方程根的分布[上学期] | 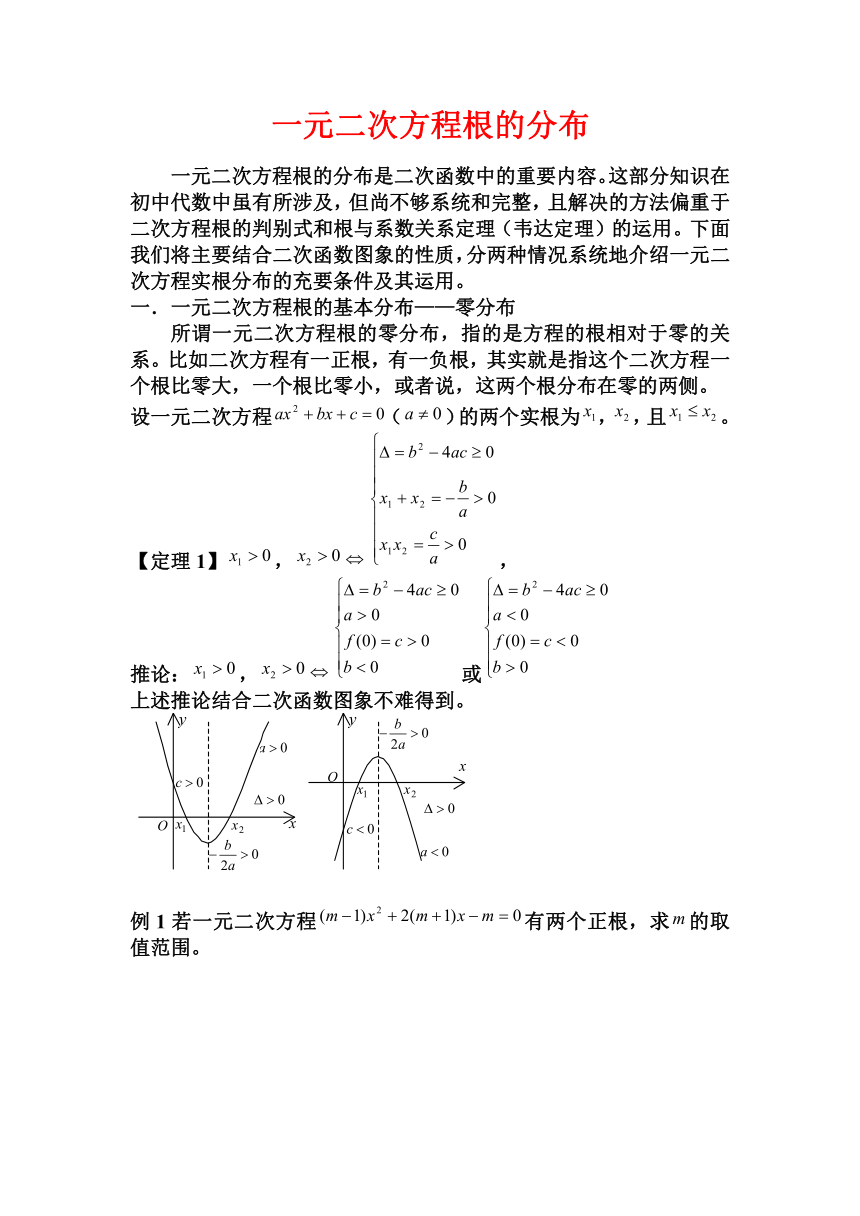 | |
| 格式 | rar | ||
| 文件大小 | 56.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-06-23 12:33:00 | ||
图片预览

文档简介
一元二次方程根的分布
一元二次方程根的分布是二次函数中的重要内容。这部分知识在初中代数中虽有所涉及,但尚不够系统和完整,且解决的方法偏重于二次方程根的判别式和根与系数关系定理(韦达定理)的运用。下面我们将主要结合二次函数图象的性质,分两种情况系统地介绍一元二次方程实根分布的充要条件及其运用。
一.一元二次方程根的基本分布——零分布
所谓一元二次方程根的零分布,指的是方程的根相对于零的关系。比如二次方程有一正根,有一负根,其实就是指这个二次方程一个根比零大,一个根比零小,或者说,这两个根分布在零的两侧。
设一元二次方程()的两个实根为,,且。
【定理1】,,
推论:,或
上述推论结合二次函数图象不难得到。
例1若一元二次方程有两个正根,求的取值范围。
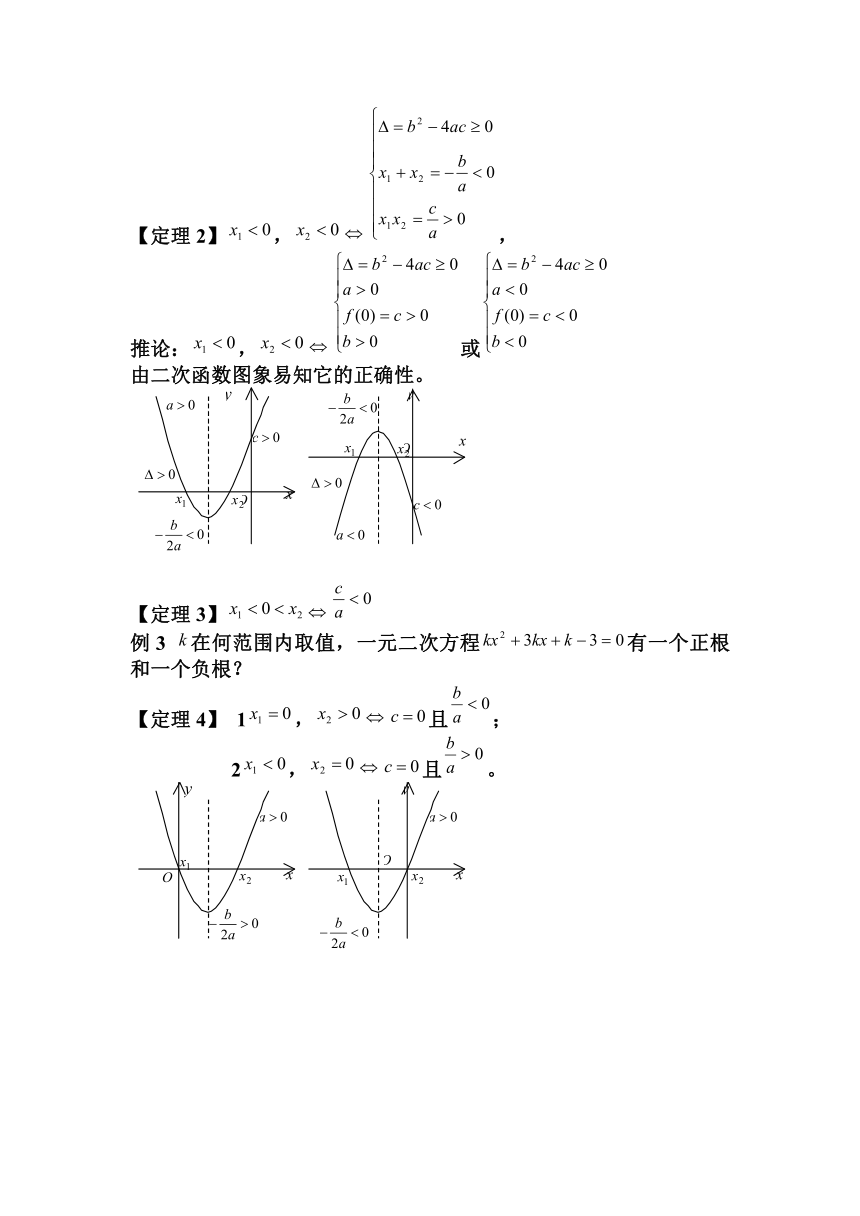
【定理2】,,
推论:,或
由二次函数图象易知它的正确性。
【定理3】
例3 在何范围内取值,一元二次方程有一个正根和一个负根?
【定理4】 1,且;
2,且。
例4若一元二次方程有一根为零,则另一根是正根还是负根?
二.一元二次方程的非零分布——分布
设一元二次方程()的两实根为,,且。为常数。则一元二次方程根的分布(即,相对于的位置)有以下若干定理。
【定理1】
【定理2】。
【定理3】。
推论1 。
推论2 。
【定理4】有且仅有(或)
【定理5】或
此定理可直接由定理4推出,请读者自证。
【定理6】或
一元二次方程根的分布是二次函数中的重要内容。这部分知识在初中代数中虽有所涉及,但尚不够系统和完整,且解决的方法偏重于二次方程根的判别式和根与系数关系定理(韦达定理)的运用。下面我们将主要结合二次函数图象的性质,分两种情况系统地介绍一元二次方程实根分布的充要条件及其运用。
一.一元二次方程根的基本分布——零分布
所谓一元二次方程根的零分布,指的是方程的根相对于零的关系。比如二次方程有一正根,有一负根,其实就是指这个二次方程一个根比零大,一个根比零小,或者说,这两个根分布在零的两侧。
设一元二次方程()的两个实根为,,且。
【定理1】,,
推论:,或
上述推论结合二次函数图象不难得到。
例1若一元二次方程有两个正根,求的取值范围。
【定理2】,,
推论:,或
由二次函数图象易知它的正确性。
【定理3】
例3 在何范围内取值,一元二次方程有一个正根和一个负根?
【定理4】 1,且;
2,且。
例4若一元二次方程有一根为零,则另一根是正根还是负根?
二.一元二次方程的非零分布——分布
设一元二次方程()的两实根为,,且。为常数。则一元二次方程根的分布(即,相对于的位置)有以下若干定理。
【定理1】
【定理2】。
【定理3】。
推论1 。
推论2 。
【定理4】有且仅有(或)
【定理5】或
此定理可直接由定理4推出,请读者自证。
【定理6】或
同课章节目录
