第5单元 整理与复习(课件)六年级上册数学人教版(共19张PPT)
文档属性
| 名称 | 第5单元 整理与复习(课件)六年级上册数学人教版(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-04 10:06:37 | ||
图片预览




文档简介
(共19张PPT)
第五单元 整理和复习
本单元你学习了圆的哪些知识?
谈话引入,初步回顾
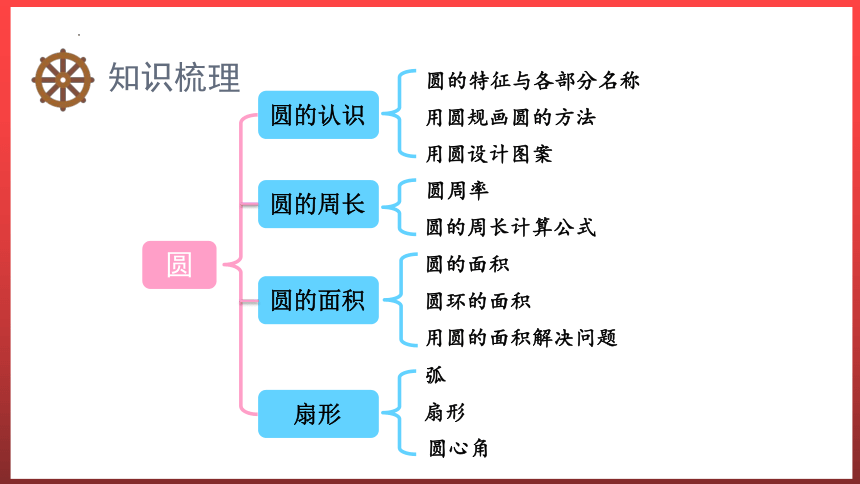
圆
圆的特征与各部分名称
用圆规画圆的方法
用圆设计图案
圆周率
圆的周长计算公式
圆的面积
圆环的面积
用圆的面积解决问题
圆的面积
圆的认识
圆的周长
扇形
弧
扇形
圆心角
圆心角
·
O
圆心
半径r
直径d
·
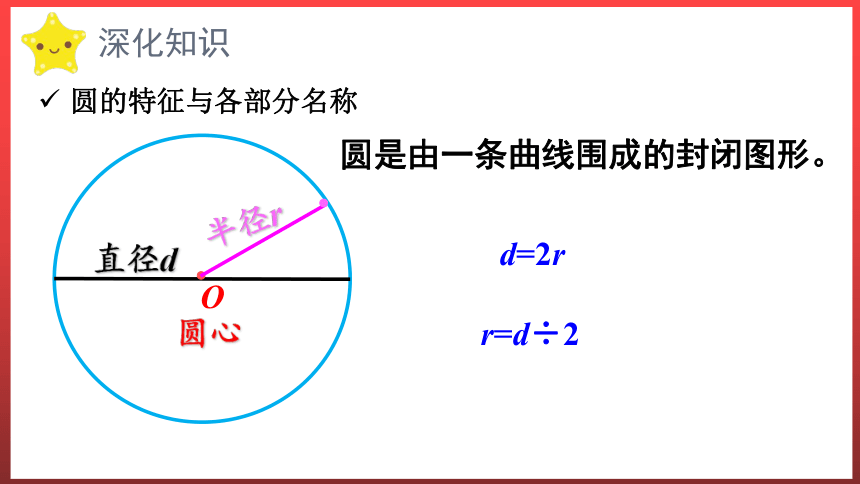
圆是由一条曲线围成的封闭图形。
d=2r
r=d÷2
圆的特征与各部分名称
深化知识
把圆沿任何一条直径对折,两边可以完全重合。
一个圆里的直径有无数条,半径有无数条,所有直径都相等,所有半径都相等,直径是半径的2倍。
圆心决定圆的位置,半径决定圆的大小。
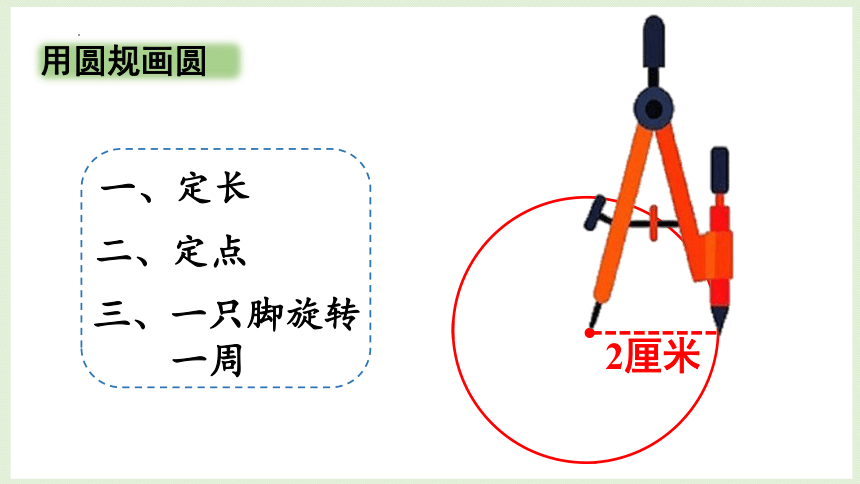
用圆规画圆的方法
(1)把圆规的两脚分开,定好两脚间的距离。
(2)把有针尖的一只脚固定在纸上。
(3)把装有铅笔的一只脚旋转一周,就画出了一个圆。
一、定长
二、定点
三、一只脚旋转
一周
2厘米
用圆规画圆
圆的周长与它的直径的比值是一个固定的数,
我们把它叫做圆周率,用字母π表示。
它是一个无限不循环小数,π=3.1415926535……
但在实际应用中常常只取它的近似值,例如π≈3.14。
如果用C表示圆的周长,就有:
C =πd
C=2πr
或
圆周率与圆的周长的计算方法
圆的面积
如果用S表示圆的面积,那么圆的面积计算公式就是 :
S=πr
=(πr)
r
C
2
外圆面积
内圆面积
圆环面积
-
=
πr
πR
S环
S环 = πR - πr
或
S环 = π(R - r )
乘法分配律
减去
得到
R
O
r
O
圆环的面积
用圆的面积解决问题
如果两个圆的半径都是r,正方形和圆之间部分的面积
左图:(2r) -3.14×r =0.86r
右图:3.14×r -( ×2r×r)×2=1.14r
2
1
弧、扇形、圆心角
A
B
O
半径
半径
弧
图上A、B两点之间的部分叫做弧,读作“弧AB”。
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
顶点在圆心的角叫做圆心角。
圆心角
1.填一填。
(1)圆心决定圆的( ),半径决定圆的( )。
(2)在同一个圆内,所有的半径都( ),所有的直径都( ),直径是半径的( ),半径与直径的比是( )。
(3)把圆规的两脚分开,使两脚的距离是4cm,这样画出的
圆的半径是( ),直径是( )。
(4)一个圆有( )条对称轴。
大小
位置
相等
相等
2倍
1:2
4cm
8cm
无数
(1)圆周率π就是3.14。( )
(2)圆的半径扩大到原来的2倍,周长和面积也扩大到原来
的2倍。( )
(3)半径相等的两个圆周长相等。( )
(4)两个圆的直径相等,它们的半径也一定相等。( )
(5)用4个圆心角都是90°的扇形,一定可以拼成一个圆。
( )
×
×
√
√
×
2.判断对错,对的画“√”,错的画“×”。
3.你见过“驴拉磨”吗?如果驴绕着一个半径为1.2m的圆走一圈,大约要走多少米?
2×3.14×1.2=7.536(m)
答:大约要走7.536米。
4.下图中的双面绣作品中间部分的画是一个直径是20 cm的圆。这幅画的面积是多少?
3.14×(20÷2) =314(cm )
答:这幅画的面积是314 cm 。
5.右图是一块玉璧,外直径18 cm,内直径7 cm。这块玉璧的面积是多少?
18÷2=9(cm)
7÷2=3.5(cm)
3.14×(9 -3.5 ) = 215.875(cm )
答:这块玉璧的面积是215.875cm 。
6.如图,学校操场的跑道由正方形的两条对边和两个半圆组成。小晨在操场上跑了5圈,一共是多少米?
(3.14×50+50×2)×5=1285(m)
答:一共是1285 米 。
50 m
操场跑道的长度等于一个整圆的周长与两条直的跑道的长度之和。
圆的面积
圆的认识
圆的周长
扇形
圆
知识总结
第五单元 整理和复习
本单元你学习了圆的哪些知识?
谈话引入,初步回顾
圆
圆的特征与各部分名称
用圆规画圆的方法
用圆设计图案
圆周率
圆的周长计算公式
圆的面积
圆环的面积
用圆的面积解决问题
圆的面积
圆的认识
圆的周长
扇形
弧
扇形
圆心角
圆心角
·
O
圆心
半径r
直径d
·
圆是由一条曲线围成的封闭图形。
d=2r
r=d÷2
圆的特征与各部分名称
深化知识
把圆沿任何一条直径对折,两边可以完全重合。
一个圆里的直径有无数条,半径有无数条,所有直径都相等,所有半径都相等,直径是半径的2倍。
圆心决定圆的位置,半径决定圆的大小。
用圆规画圆的方法
(1)把圆规的两脚分开,定好两脚间的距离。
(2)把有针尖的一只脚固定在纸上。
(3)把装有铅笔的一只脚旋转一周,就画出了一个圆。
一、定长
二、定点
三、一只脚旋转
一周
2厘米
用圆规画圆
圆的周长与它的直径的比值是一个固定的数,
我们把它叫做圆周率,用字母π表示。
它是一个无限不循环小数,π=3.1415926535……
但在实际应用中常常只取它的近似值,例如π≈3.14。
如果用C表示圆的周长,就有:
C =πd
C=2πr
或
圆周率与圆的周长的计算方法
圆的面积
如果用S表示圆的面积,那么圆的面积计算公式就是 :
S=πr
=(πr)
r
C
2
外圆面积
内圆面积
圆环面积
-
=
πr
πR
S环
S环 = πR - πr
或
S环 = π(R - r )
乘法分配律
减去
得到
R
O
r
O
圆环的面积
用圆的面积解决问题
如果两个圆的半径都是r,正方形和圆之间部分的面积
左图:(2r) -3.14×r =0.86r
右图:3.14×r -( ×2r×r)×2=1.14r
2
1
弧、扇形、圆心角
A
B
O
半径
半径
弧
图上A、B两点之间的部分叫做弧,读作“弧AB”。
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
顶点在圆心的角叫做圆心角。
圆心角
1.填一填。
(1)圆心决定圆的( ),半径决定圆的( )。
(2)在同一个圆内,所有的半径都( ),所有的直径都( ),直径是半径的( ),半径与直径的比是( )。
(3)把圆规的两脚分开,使两脚的距离是4cm,这样画出的
圆的半径是( ),直径是( )。
(4)一个圆有( )条对称轴。
大小
位置
相等
相等
2倍
1:2
4cm
8cm
无数
(1)圆周率π就是3.14。( )
(2)圆的半径扩大到原来的2倍,周长和面积也扩大到原来
的2倍。( )
(3)半径相等的两个圆周长相等。( )
(4)两个圆的直径相等,它们的半径也一定相等。( )
(5)用4个圆心角都是90°的扇形,一定可以拼成一个圆。
( )
×
×
√
√
×
2.判断对错,对的画“√”,错的画“×”。
3.你见过“驴拉磨”吗?如果驴绕着一个半径为1.2m的圆走一圈,大约要走多少米?
2×3.14×1.2=7.536(m)
答:大约要走7.536米。
4.下图中的双面绣作品中间部分的画是一个直径是20 cm的圆。这幅画的面积是多少?
3.14×(20÷2) =314(cm )
答:这幅画的面积是314 cm 。
5.右图是一块玉璧,外直径18 cm,内直径7 cm。这块玉璧的面积是多少?
18÷2=9(cm)
7÷2=3.5(cm)
3.14×(9 -3.5 ) = 215.875(cm )
答:这块玉璧的面积是215.875cm 。
6.如图,学校操场的跑道由正方形的两条对边和两个半圆组成。小晨在操场上跑了5圈,一共是多少米?
(3.14×50+50×2)×5=1285(m)
答:一共是1285 米 。
50 m
操场跑道的长度等于一个整圆的周长与两条直的跑道的长度之和。
圆的面积
圆的认识
圆的周长
扇形
圆
知识总结
