【中学教材全解】2013-2014学年(北师版选修2-1)模块检测(含答案解析)
文档属性
| 名称 | 【中学教材全解】2013-2014学年(北师版选修2-1)模块检测(含答案解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 202.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-11-27 00:00:00 | ||
图片预览




文档简介
选修2-1模块检测(北京师大版)
建议用时 实际用时 满分 实际得分
120分钟 150分
一、选择题(每小题5分,共60分)
1. 若点P到直线x=-1的距离比它到点(2,0)的距离小1,则点P的轨迹为( )
A.圆 B.椭圆
C.双曲线 D.抛物线
2.已知p:|x+1|≤4;q:<5x-6,则p是q成立的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分又不必要条件
3. 设 ,若是的必要不充分条件,则实数的
取值范围是( )
A. B.
C. D.
4. 已知点P是直线2x-y+3=0上的一个动点,定点M(-1,2),Q是线段PM延长线上的一点,且|PM|=|MQ|,则点Q的轨迹方程是( )
A.2x+y+1=0
B.2x-y-5=0
C.2x-y-1=0
D.2x-y+5=0
5. 若AB是过椭圆 (a>b>0)中心的一条弦,M是椭圆上任意一点,且AM,BM与坐标轴不平行,kAM,kBM分别表示直线AM,BM的斜率,则kAM kBM=( )
A. B.
C. D.
6. 在正方体ABCDA1B1C1D1中,O是底面ABCD的中心,M,N分别是棱DD1,D1C1的中点,则直线OM( )
A.和AC,MN都垂直
B.垂直于AC,但不垂直于MN
C.垂直于MN,但不垂直于AC
D.与AC,MN都不垂直
7. 如图,在空间直角坐标系中,正方体棱长为2,点E是棱AB的中点,点F(0,y,z)是正方体的面AA1D1D上一点,且CF⊥B1E,则点
F(0,y,z)满足方程( )
A.y-z=0
B.2y-z-1=0
C.2y-z-2=0
D.z-1=0
8. 圆心在抛物线()上,并且与抛物线的准线及轴都相切的圆的方程是( )
A.
B.
C.
D.
9. 给出下列命题:
①若“”是假命题,则是真 命题;
②;
③若关于的实系数一元二次不等式的解集为,则必有且;
④
其中真命题的个数是( )
A.1 B.2 C.3 D.4
10. 设双曲线的半焦距为,直线过两点.已知原点到直线的距离为,则双曲线的离心率为( )
A.2 B. C. D.
11. 已知△ABC的顶点A(-5,0)、B(5,0),△ABC的内切圆圆心在直线x=3上,则顶点C的轨迹方程是( )
A. B.
C.(x>3) D. (x>4)
12. 已知抛物线上一点0到其焦点的距离为5,双曲线的左顶点为,若双曲线的一条渐近线与直线平行,则实数的值是( )
A. B. C. D.
二、填空题(每小题5分,共20分)
13. 已知命题“存在,使”是假命题,则实数的取值范围是________.
14. 下列四个结论中,正确的有 (填序号).
①若A是B的必要不充分条件,则非B也是非A的必要不充分条件;
②“是“一元二次不等式a+bx+c≥0的解集为R”的充要条件;
③“x≠1”是“≠1”的充分不必要条件;
④“x≠0”是“x+|x|>0”的必要不充分条件.
15. 在三棱锥PABC中,AB⊥BC,AB=BC=PA,点O、D分别是AC、PC的中点,OP⊥底面ABC,则直线OD与平面PBC所成角的正弦值是 .
16. 若点O和点F分别为椭圆的中心和左焦点,点P为椭圆上的任意一点,则的最大值为
三、解答题(共70分)
17. (12分)已知四棱锥的底面为直角梯形,,底面,且,,点是的中点.
(1)证明:平面平面;
求与所成角的余弦值
(3)求平面与平面所成二面角的平面角的余弦值.
18.(12分)设p:实数x满足-4ax+3<0,其中a>0;q:实数x满足
(1)若a=1,且p∧q为真,求实数x的取值范围;
若p是q的充分不必要条件,求实数a的取值范围
19.(14分)已知椭圆的离心率,过点和的直线与原点的距离为.
(1)求椭圆的方程.
(2)已知定点,若直线 与椭圆交于两点.问:是否存在,使以为直径的圆过 请说明理由.
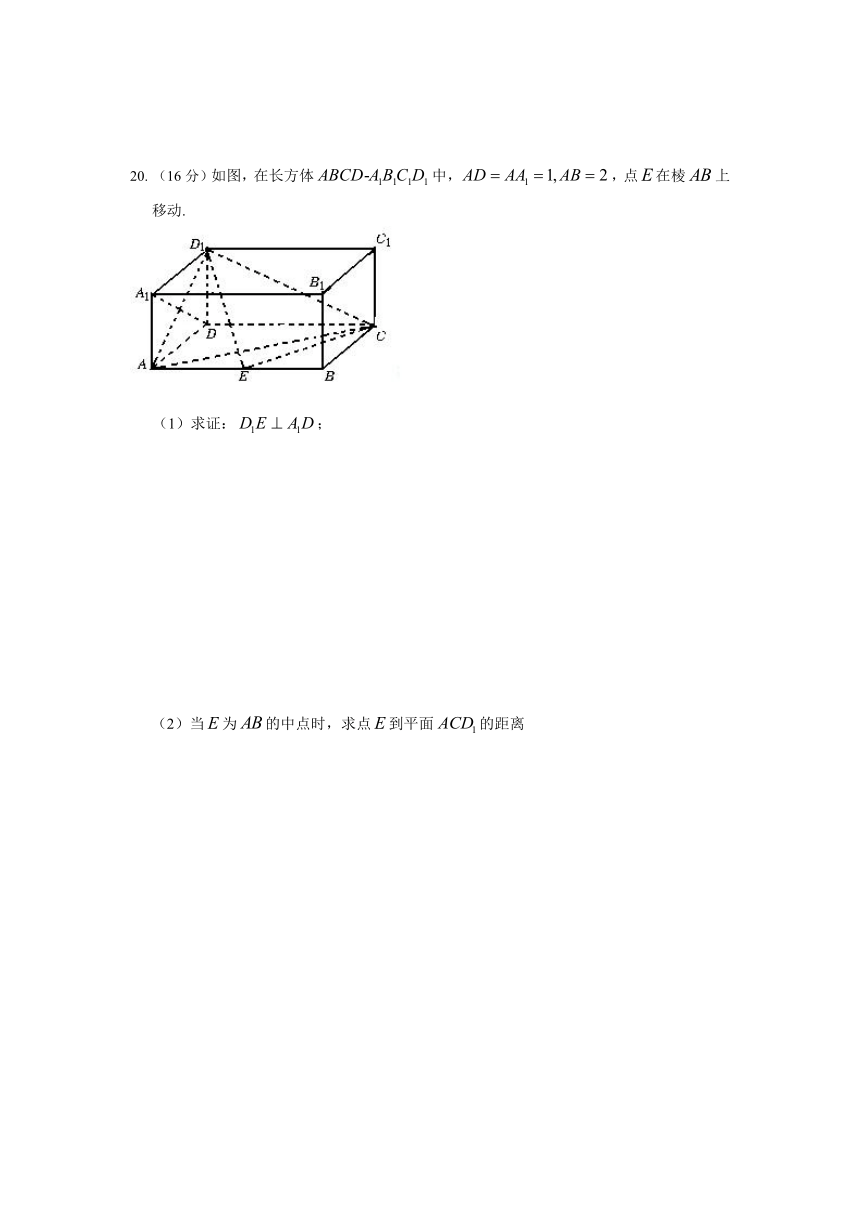
20. (16分)如图,在长方体中,,点在棱上移动.
(1)求证:;
(2)当为的中点时,求点到平面的距离
(3)当为何值时,二面角 的大小为?
21. (16分)设分别为椭圆: 的左、右两个焦点.
(1)若椭圆上的点到两点的距离之和等于,写出椭圆的方程和焦点坐标.
(2)设点是(1)中所得椭圆上的动点,求线段的中点的轨迹方程.
(3)已知椭圆具有性质:若是椭圆上关于原点对称的两个点,点是椭圆上任意一点,当直线、的斜率都存在,并记为、时,那么与之积是与点位置无关的定值.试对双曲线写出类似的性质,并加以证明
一、选择题
1. D 解析:由题意知,点P到点(2,0)的距离与点P到直线x=-2的距离相等,由抛物线定义得点P的轨迹是以(2,0)为焦点,以直线x=-2为准线的抛物线,故选D.
2. B 解析:由|x+1|≤4-4≤x+1≤4,得-5≤x≤3,即p对应的集合为[-5,3];由<5x-6-5x+6<0,解一元二次不等式可得2<x<3,即q对应的集合为(2,3).因为(2,3)[-5,3],所以p是q成立的必要不充分条件.
3. A 解析:由已知得若成立,则,若成立,则.又﹁p是﹁q的必要不充分条件,即q是p的必要不充分条件,所以所以.
4. D 解析:设点Q(x,y),则点P为(-2-x,4-y),代入2x-y+3=0得2x-y+5=0.
5. B 解析:设A(x1,y1),M(x0,y0),则B(x1,y1),则kAM kBM=.
∵ A,M在椭圆上,∴ ,两式相减,可得kAM kBM= ,故选B.
6. A 解析:以DA,DC,DD1所在的直线为x轴,y轴,z轴建立空间直角坐标系.
设正方体的棱长为2a,则D(0,0,0),D1(0,0,2a),M(0,0,a),A(2a,0,0),C(0,2a,0),O(a,a,0),N(0,a,2a),
∴ =(-a,-a,a), =(0,a,a),=(-2a,2a,0).
∴ =0, =0,
∴ OM⊥AC,OM⊥MN.故选A.
7. D 解析:如题图所示,由已知可得E(1,0,0),B1(2,0,2),C(2,2,0),
所以 =(-1,0,-2),=(-2,y-2,z).
因为CF⊥B1E,所以 =0.
即2-2z=0,即z=1.故选D.
8. D 解析:抛物线的焦点坐标为,由圆心在抛物线上,且与轴和该抛物线的准线都相切以及抛物线的定义可知,所求圆的圆心的横坐标,即圆心是,半径长是1,故所求圆的方程为.
9. B 解析:“p或q”是假命题,则它的否定是真命题,即“﹁p且﹁q”是真命题,①是真命题;若,若,则,所以②是真命题;若一元二次不等式的解集是,则必有且,所以③是假命题;当时,必有但当y=5时,满足但,所以④是假命题.共有2个真命题.
10. A 解析:由已知,直线的方程为.原点到直线的距离为,则有.
又,所以,两边平方,得.两边同除以,并整理,得 ,所以或.而,得>2,所以.故(负
值舍去).
11. C 解析:如图,|AD|=|AE|=8,|BF|=|BE|=2,|CD|=|CF|,
所以|CA|-|CB|=8-2=6.
根据双曲线的定义,所求轨迹是以A、B为焦点,实轴长为6的双曲线的右支(除与轴的交点外),
所以顶点C的轨迹方程为(x>3).
12. B 解析:依题意知,所以,所以,所以,点的坐标为.
又,所以直线的斜率为.由题意得,解得.
二、填空题
13. 解析:已知命题是假命题,则原命题的否定“对任意,使”是真命题,所以,解得.
14. ①②④ 解析:∵ 原命题与其逆否命题等价,∴ 若A是B的必要不充分条件,则非B也是非A的必要不充分条件.
x≠1≠1,反例:x=-1=1,
∴“x≠1”是“≠1”的不充分条件.
x≠0x+|x|>0,反例:x=-2x+|x|=0.
但x+|x|>0x>0x≠0,
∴“x≠0”是“x+|x|>0”的必要不充分条件.
15. D 解析:
EMBED Equation.DSMT4 \* MERGEFORMAT
16. 6 解析:由题意,得F(-1,0),
设点,,则有 =1,解得=.
因为=,,=,,
所以
此二次函数对应的抛物线的对称轴为直线=-2,
因为-2≤≤2,所以当=2时,取得最大值6.
三、解答题
17. (1)证明:如图,以为坐标原点,长为单位长度,建立
空间直角坐标系,则各点坐标为
.
因为
由题设知,且与是平面内的两条相交直线,
由此得平面.
又在平面内,故平面⊥平面.
(2)解:因为
故AC与PB所成角的余弦值为.
(3)解:在上取一点,则存在使
要使
为所求二面角的平面角.
18. 解:由-4ax+3<0,得(x-3a)(x-a)<0.
又a>0,所以a<x<3a.
(1)当a=1时,1<x<3,
即p为真时实数x的取值范围是1<x<3.
由
得2<x≤3,
即q为真时实数x的取值范围是2<x≤3.
若p∧q为真,则p真q真,
所以实数x的取值范围是2<x<3.
(2)若p是q的充分不必要条件,
即q,且p.
设A={x|p},B={x|q},则AB.
又A={x|p}={x|x≤a或x≥3a},
B={x|q}={x|x≤2或x>3},
则有0<a≤2且3a>3,
所以实数a的取值范围是1<a≤2.
19. 解:(1)因为直线的方程为,
依题意得解得所以椭圆方程为.
(2)假设存在这样的值,由得,
所以.①
设、,则②
而.
当且仅当时,以为直径的圆过点,则,
即,
所以. ③
将②式代入③式整理解得.经验证,使①式成立.
综上可知,存在,使得以为直径的圆过点.
20. (1)证明:如图,以为坐标原点,直线分别为轴,建立空间直角坐标系,
设,则,
(2)解:因为为的中点,则,
从而,.
设平面的法向量为,
则
即得
令b=1,从而,
所以点到平面的距离为
(3)解:设,平面的法向量,
所以
由
令,
所以
依题意
所以(不合题意,舍去),.
所以当时,二面角的大小为.
21. 解:(1)由题意知,椭圆的焦点在轴上.
由椭圆上的点到两点的距离之和是4,得,即.
又点在椭圆上,
因此,得,于是.
所以椭圆的方程为,焦点,.
(2)设椭圆上的动点,线段的中点满足,
即,.
因此,即为所求的轨迹方程.
(3)类似的性质为:若是双曲线上关于原点对称的两个点,点是双曲线上任意一点,
当直线的斜率都存在,并记为时,那么与之积是与点位置无关的定值.
证明如下:设点的坐标为,则点的坐标为,其中.
又设点的坐标为,由,
得.
将代入得
建议用时 实际用时 满分 实际得分
120分钟 150分
一、选择题(每小题5分,共60分)
1. 若点P到直线x=-1的距离比它到点(2,0)的距离小1,则点P的轨迹为( )
A.圆 B.椭圆
C.双曲线 D.抛物线
2.已知p:|x+1|≤4;q:<5x-6,则p是q成立的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分又不必要条件
3. 设 ,若是的必要不充分条件,则实数的
取值范围是( )
A. B.
C. D.
4. 已知点P是直线2x-y+3=0上的一个动点,定点M(-1,2),Q是线段PM延长线上的一点,且|PM|=|MQ|,则点Q的轨迹方程是( )
A.2x+y+1=0
B.2x-y-5=0
C.2x-y-1=0
D.2x-y+5=0
5. 若AB是过椭圆 (a>b>0)中心的一条弦,M是椭圆上任意一点,且AM,BM与坐标轴不平行,kAM,kBM分别表示直线AM,BM的斜率,则kAM kBM=( )
A. B.
C. D.
6. 在正方体ABCDA1B1C1D1中,O是底面ABCD的中心,M,N分别是棱DD1,D1C1的中点,则直线OM( )
A.和AC,MN都垂直
B.垂直于AC,但不垂直于MN
C.垂直于MN,但不垂直于AC
D.与AC,MN都不垂直
7. 如图,在空间直角坐标系中,正方体棱长为2,点E是棱AB的中点,点F(0,y,z)是正方体的面AA1D1D上一点,且CF⊥B1E,则点
F(0,y,z)满足方程( )
A.y-z=0
B.2y-z-1=0
C.2y-z-2=0
D.z-1=0
8. 圆心在抛物线()上,并且与抛物线的准线及轴都相切的圆的方程是( )
A.
B.
C.
D.
9. 给出下列命题:
①若“”是假命题,则是真 命题;
②;
③若关于的实系数一元二次不等式的解集为,则必有且;
④
其中真命题的个数是( )
A.1 B.2 C.3 D.4
10. 设双曲线的半焦距为,直线过两点.已知原点到直线的距离为,则双曲线的离心率为( )
A.2 B. C. D.
11. 已知△ABC的顶点A(-5,0)、B(5,0),△ABC的内切圆圆心在直线x=3上,则顶点C的轨迹方程是( )
A. B.
C.(x>3) D. (x>4)
12. 已知抛物线上一点0到其焦点的距离为5,双曲线的左顶点为,若双曲线的一条渐近线与直线平行,则实数的值是( )
A. B. C. D.
二、填空题(每小题5分,共20分)
13. 已知命题“存在,使”是假命题,则实数的取值范围是________.
14. 下列四个结论中,正确的有 (填序号).
①若A是B的必要不充分条件,则非B也是非A的必要不充分条件;
②“是“一元二次不等式a+bx+c≥0的解集为R”的充要条件;
③“x≠1”是“≠1”的充分不必要条件;
④“x≠0”是“x+|x|>0”的必要不充分条件.
15. 在三棱锥PABC中,AB⊥BC,AB=BC=PA,点O、D分别是AC、PC的中点,OP⊥底面ABC,则直线OD与平面PBC所成角的正弦值是 .
16. 若点O和点F分别为椭圆的中心和左焦点,点P为椭圆上的任意一点,则的最大值为
三、解答题(共70分)
17. (12分)已知四棱锥的底面为直角梯形,,底面,且,,点是的中点.
(1)证明:平面平面;
求与所成角的余弦值
(3)求平面与平面所成二面角的平面角的余弦值.
18.(12分)设p:实数x满足-4ax+3<0,其中a>0;q:实数x满足
(1)若a=1,且p∧q为真,求实数x的取值范围;
若p是q的充分不必要条件,求实数a的取值范围
19.(14分)已知椭圆的离心率,过点和的直线与原点的距离为.
(1)求椭圆的方程.
(2)已知定点,若直线 与椭圆交于两点.问:是否存在,使以为直径的圆过 请说明理由.
20. (16分)如图,在长方体中,,点在棱上移动.
(1)求证:;
(2)当为的中点时,求点到平面的距离
(3)当为何值时,二面角 的大小为?
21. (16分)设分别为椭圆: 的左、右两个焦点.
(1)若椭圆上的点到两点的距离之和等于,写出椭圆的方程和焦点坐标.
(2)设点是(1)中所得椭圆上的动点,求线段的中点的轨迹方程.
(3)已知椭圆具有性质:若是椭圆上关于原点对称的两个点,点是椭圆上任意一点,当直线、的斜率都存在,并记为、时,那么与之积是与点位置无关的定值.试对双曲线写出类似的性质,并加以证明
一、选择题
1. D 解析:由题意知,点P到点(2,0)的距离与点P到直线x=-2的距离相等,由抛物线定义得点P的轨迹是以(2,0)为焦点,以直线x=-2为准线的抛物线,故选D.
2. B 解析:由|x+1|≤4-4≤x+1≤4,得-5≤x≤3,即p对应的集合为[-5,3];由<5x-6-5x+6<0,解一元二次不等式可得2<x<3,即q对应的集合为(2,3).因为(2,3)[-5,3],所以p是q成立的必要不充分条件.
3. A 解析:由已知得若成立,则,若成立,则.又﹁p是﹁q的必要不充分条件,即q是p的必要不充分条件,所以所以.
4. D 解析:设点Q(x,y),则点P为(-2-x,4-y),代入2x-y+3=0得2x-y+5=0.
5. B 解析:设A(x1,y1),M(x0,y0),则B(x1,y1),则kAM kBM=.
∵ A,M在椭圆上,∴ ,两式相减,可得kAM kBM= ,故选B.
6. A 解析:以DA,DC,DD1所在的直线为x轴,y轴,z轴建立空间直角坐标系.
设正方体的棱长为2a,则D(0,0,0),D1(0,0,2a),M(0,0,a),A(2a,0,0),C(0,2a,0),O(a,a,0),N(0,a,2a),
∴ =(-a,-a,a), =(0,a,a),=(-2a,2a,0).
∴ =0, =0,
∴ OM⊥AC,OM⊥MN.故选A.
7. D 解析:如题图所示,由已知可得E(1,0,0),B1(2,0,2),C(2,2,0),
所以 =(-1,0,-2),=(-2,y-2,z).
因为CF⊥B1E,所以 =0.
即2-2z=0,即z=1.故选D.
8. D 解析:抛物线的焦点坐标为,由圆心在抛物线上,且与轴和该抛物线的准线都相切以及抛物线的定义可知,所求圆的圆心的横坐标,即圆心是,半径长是1,故所求圆的方程为.
9. B 解析:“p或q”是假命题,则它的否定是真命题,即“﹁p且﹁q”是真命题,①是真命题;若,若,则,所以②是真命题;若一元二次不等式的解集是,则必有且,所以③是假命题;当时,必有但当y=5时,满足但,所以④是假命题.共有2个真命题.
10. A 解析:由已知,直线的方程为.原点到直线的距离为,则有.
又,所以,两边平方,得.两边同除以,并整理,得 ,所以或.而,得>2,所以.故(负
值舍去).
11. C 解析:如图,|AD|=|AE|=8,|BF|=|BE|=2,|CD|=|CF|,
所以|CA|-|CB|=8-2=6.
根据双曲线的定义,所求轨迹是以A、B为焦点,实轴长为6的双曲线的右支(除与轴的交点外),
所以顶点C的轨迹方程为(x>3).
12. B 解析:依题意知,所以,所以,所以,点的坐标为.
又,所以直线的斜率为.由题意得,解得.
二、填空题
13. 解析:已知命题是假命题,则原命题的否定“对任意,使”是真命题,所以,解得.
14. ①②④ 解析:∵ 原命题与其逆否命题等价,∴ 若A是B的必要不充分条件,则非B也是非A的必要不充分条件.
x≠1≠1,反例:x=-1=1,
∴“x≠1”是“≠1”的不充分条件.
x≠0x+|x|>0,反例:x=-2x+|x|=0.
但x+|x|>0x>0x≠0,
∴“x≠0”是“x+|x|>0”的必要不充分条件.
15. D 解析:
EMBED Equation.DSMT4 \* MERGEFORMAT
16. 6 解析:由题意,得F(-1,0),
设点,,则有 =1,解得=.
因为=,,=,,
所以
此二次函数对应的抛物线的对称轴为直线=-2,
因为-2≤≤2,所以当=2时,取得最大值6.
三、解答题
17. (1)证明:如图,以为坐标原点,长为单位长度,建立
空间直角坐标系,则各点坐标为
.
因为
由题设知,且与是平面内的两条相交直线,
由此得平面.
又在平面内,故平面⊥平面.
(2)解:因为
故AC与PB所成角的余弦值为.
(3)解:在上取一点,则存在使
要使
为所求二面角的平面角.
18. 解:由-4ax+3<0,得(x-3a)(x-a)<0.
又a>0,所以a<x<3a.
(1)当a=1时,1<x<3,
即p为真时实数x的取值范围是1<x<3.
由
得2<x≤3,
即q为真时实数x的取值范围是2<x≤3.
若p∧q为真,则p真q真,
所以实数x的取值范围是2<x<3.
(2)若p是q的充分不必要条件,
即q,且p.
设A={x|p},B={x|q},则AB.
又A={x|p}={x|x≤a或x≥3a},
B={x|q}={x|x≤2或x>3},
则有0<a≤2且3a>3,
所以实数a的取值范围是1<a≤2.
19. 解:(1)因为直线的方程为,
依题意得解得所以椭圆方程为.
(2)假设存在这样的值,由得,
所以.①
设、,则②
而.
当且仅当时,以为直径的圆过点,则,
即,
所以. ③
将②式代入③式整理解得.经验证,使①式成立.
综上可知,存在,使得以为直径的圆过点.
20. (1)证明:如图,以为坐标原点,直线分别为轴,建立空间直角坐标系,
设,则,
(2)解:因为为的中点,则,
从而,.
设平面的法向量为,
则
即得
令b=1,从而,
所以点到平面的距离为
(3)解:设,平面的法向量,
所以
由
令,
所以
依题意
所以(不合题意,舍去),.
所以当时,二面角的大小为.
21. 解:(1)由题意知,椭圆的焦点在轴上.
由椭圆上的点到两点的距离之和是4,得,即.
又点在椭圆上,
因此,得,于是.
所以椭圆的方程为,焦点,.
(2)设椭圆上的动点,线段的中点满足,
即,.
因此,即为所求的轨迹方程.
(3)类似的性质为:若是双曲线上关于原点对称的两个点,点是双曲线上任意一点,
当直线的斜率都存在,并记为时,那么与之积是与点位置无关的定值.
证明如下:设点的坐标为,则点的坐标为,其中.
又设点的坐标为,由,
得.
将代入得
同课章节目录
