人教版数学八年级上册 12.4 全等三角形小结第3课时 课件(共23张PPT)
文档属性
| 名称 | 人教版数学八年级上册 12.4 全等三角形小结第3课时 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 498.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-04 15:45:24 | ||
图片预览





文档简介
(共23张PPT)
第3课时
12.4 全等三角形小结
八年级上册 RJ
初中数学
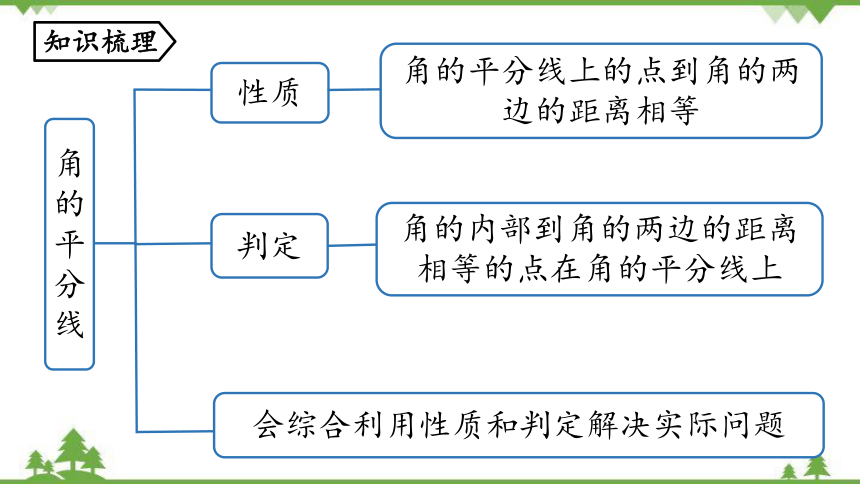
角的平分线
性质
判定
会综合利用性质和判定解决实际问题
角的平分线上的点到角的两边的距离相等
角的内部到角的两边的距离相等的点在角的平分线上
知识梳理
角的平分线
1.作已知角的平分线
(1)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
(2)分别以M,N为圆心,大于 MN
的长为半径画弧,两弧在∠AOB的内部
相交于点C.
C
B
N
O
M
A
(3)画射线OC,射线OC即为所求.
2.角的平分线的性质
角的平分线上的点到角的两边的距离相等.
几何表示:如图,∵OC是∠AOB的平分线,P是OC上一点,PD⊥OA,PE⊥OB,垂足分别为D,E.
∴PD=PE.
3.证明几何命题的一般步骤
(1)明确一个命题中的已知和求证;
(2)根据题意,画出图形,并用符号表示已知和求证;
(3)经过分析,找出由已知推出要证明的结论的途径,写出证明的过程.
4.角的平分线的判定
角的内部到角的两边的距离相等的点在角的平分线上.
几何表示:如图,∵点P是∠AOB内的一点,PD⊥OA,PE⊥OB,垂足分别为D,E,且PD=PE.
∴点P在∠AOB的平分线OC上.
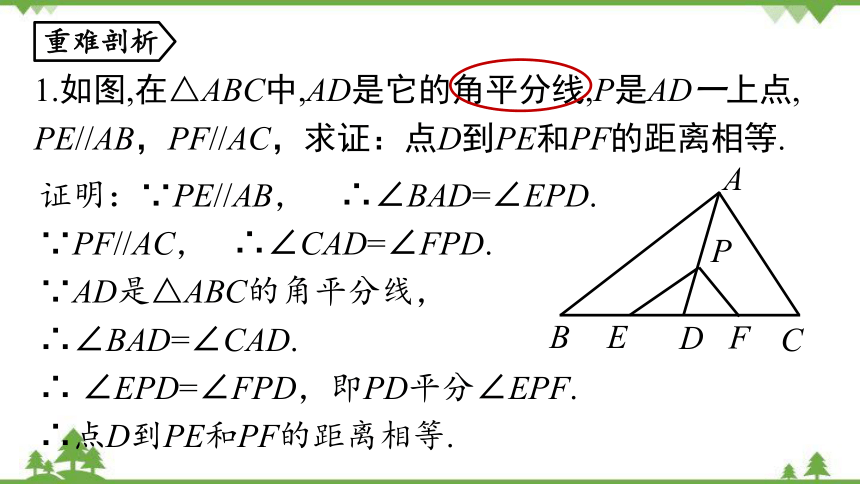
1.如图,在△ABC中,AD是它的角平分线,P是AD一上点,
PE//AB,PF//AC,求证:点D到PE和PF的距离相等.
证明:∵PE//AB, ∴∠BAD=∠EPD.
∵PF//AC, ∴∠CAD=∠FPD.
∵AD是△ABC的角平分线,
∴∠BAD=∠CAD.
∴ ∠EPD=∠FPD,即PD平分∠EPF.
∴点D到PE和PF的距离相等.
C
A
E
F
D
P
B
重难剖析
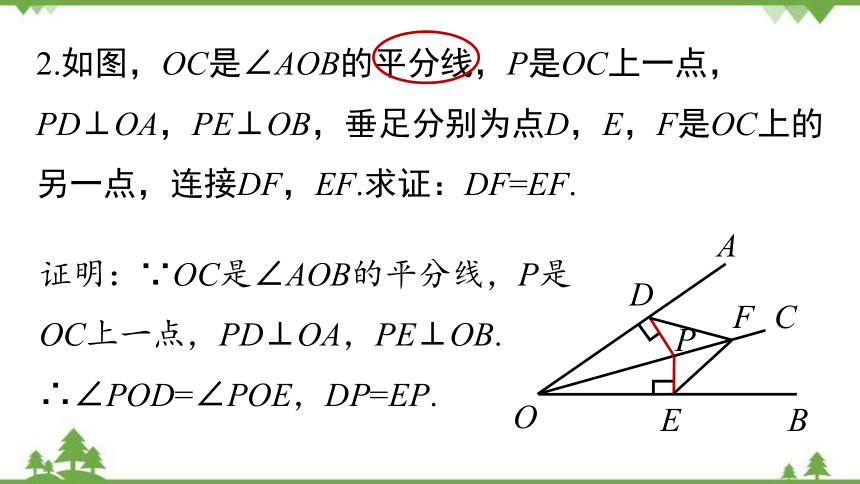
2.如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA,PE⊥OB,垂足分别为点D,E,F是OC上的另一点,连接DF,EF.求证:DF=EF.
┐
O
B
A
C
P
E
D
┐
F
证明:∵OC是∠AOB的平分线,P是OC上一点,PD⊥OA,PE⊥OB.
∴∠POD=∠POE,DP=EP.
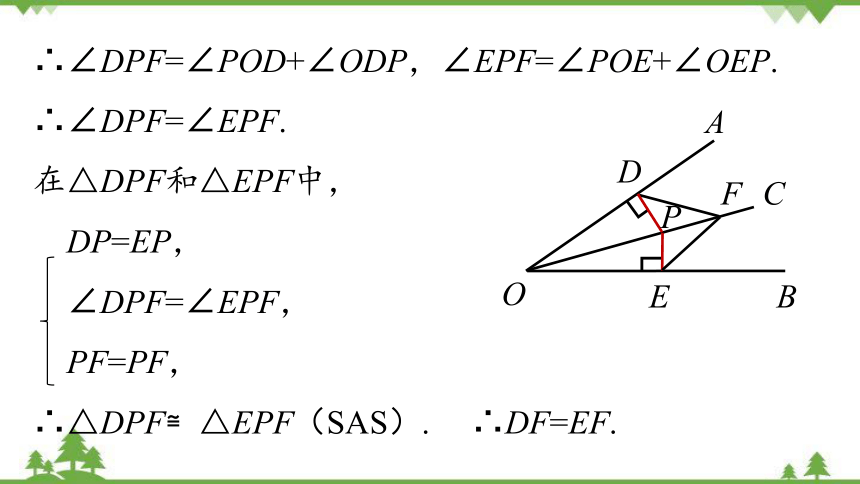
∴∠DPF=∠POD+∠ODP,∠EPF=∠POE+∠OEP.
∴∠DPF=∠EPF.
在△DPF和△EPF中,
DP=EP,
∠DPF=∠EPF,
PF=PF,
∴△DPF≌△EPF(SAS). ∴DF=EF.
┐
O
B
A
C
P
E
D
┐
F
3.证明:如果两个三角形有两条边和其中一条边上的中线分别相等,那么这两个三角形全等.
已知:如图,在△ABC和△DEF中,AC=DF,BC=EF,AM,DN分别为△ABC和△DEF的中线,且AM=DN.
求证:△ABC≌△DEF.
A
B
C
D
E
F
M
N
证明:∵BC=EF,AM,DN分别为△ABC和△DEF的中线, ∴CM=FN.
∵在△ACM和△DFN中, AM=DN,
AC=DF,
CM=FN,
∴△ACM≌△DFN. ∴∠C=∠F.
A
B
C
D
E
F
M
N
∵在△ABC和△DEF中, AC=DF,
∠C=∠F,
BC=EF,
∴△ABC≌△DEF.
A
B
C
D
E
F
M
N
4.如图,在△ABC中,AD是它的角平分线.求证:S△ABD:S△ACD=AB: AC.
证明:过点D作DE⊥AB,DF⊥AC,
垂足分别为E,F.
∵AD是△ABC的角平分线,∴DE=DF.
又∵S△ABD= AB DE,S△ACD= AC DF,
∴S△ABD:S△ACD=AB:AC.
A
B
C
D
E
F
┐
┐
1.如图,在四边形ABCD中,∠B=90°,AB//CD,M是BC的中点,AM平分∠DAB.
(1)DM是否平分∠ADC?请证明你的结论.
(2)线段DM与AM有怎样的位置关系?
请说明理由.
能力提升
判断两条线段的位置关系时,一般不是平行就是垂直,可先从这两种情况思考
E
解:(1)DM平分∠ADC. 证明如下:
如图,过点M作ME⊥AD,垂足为E.
∵∠B=90°,∴MB⊥AB.
∵AM平分∠DAB,MB⊥AB,ME⊥AD,
∴MB=ME. ∵∠B=90°,AB//CD.
∴∠C=90°,即MC⊥CD.
∵M为BC的中点, ∴MC=MB. ∴ME=MC.
∴DM平分∠ADC.
┐
E
(2)DM⊥AM. 理由如下:
∵AB//CD,∴∠CDA+∠BAD=180°.
又∵∠EDM=∠CDM= ∠CDA,
∠EAM=∠BAM= ∠BAD,
∴∠MDA+∠MAD= (∠CDA+∠BAD)=90°.
∴∠DMA=90°. ∴DM⊥AM.
┐
2.如图(1),在△ABC中,点D在边BC上,DE⊥AB,DF⊥AC,垂足分别为E,F,请你添加一个条件使得AD⊥EF.
(1)你添加的条件是 ,并证明AD⊥EF.
注意答案不唯一,可多思考几种答案
解:(1)AD平分∠BAC(答案不唯一),证明如下:
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF.
在Rt△ADE和Rt△ADF中, AD=AD,
DE=DF,
∴Rt△ADE≌Rt△ADF(HL).
∴∠EDA=∠FDA.
设AD交EF于点O,
在△DOE和△DOF中, DE=DF,
∠EDO=∠FDO,
DO=DO,
∴△DOE≌△DOF. ∴∠DOE=∠DOF.
∵∠DOE+∠DOF=180°.
∴∠DOE=∠DOF=90°,即AD⊥EF.
(2)如图(2),AD为∠BAC的平分线,当有一点G从点D向点A运动时,GE⊥AB,GF⊥AC,垂足分别为E,F.这时AD是否垂直于EF?
(3)如图(3),当点G从点D出发沿着AD方向运动时,其他条件同(2),这时AD是否垂直于EF?
(2)AD⊥EF,证明方法同(1).
(3)AD⊥EF,证明方法同(1).
由本题可以得出一般结论:从角平分线上一点向角两边引垂线,垂足的连线被角平分线垂直平分.
3.如图,点C在线段AB上,AD//EB,AC=BE,AD=BC
CF平分∠DCE.试探索CF和DE的位置关系,并说明理由.
解:CF⊥DE,证明如下:
∵AD//EB, ∴∠A=∠B.
在△ACD和△BEC中, AD=BC,
∠A=∠B,
AC=BE,
∴△ACD≌△BEC(SAS). ∴CD=EC.
A
B
C
D
E
F
∵CF平分∠DCE,∴∠DCF=∠ECF.
在△DCF和△ECF中, CD=CE,
∠DCF=∠ECF,
CF=CF,
∴△DCF≌△ECF(SAS).
∴∠CFD=∠CFE.
∵∠CFD+∠CFE=180°,
∴∠CFD=∠CFE=90°.
∴CF⊥DE.
A
B
C
D
E
F
第3课时
12.4 全等三角形小结
八年级上册 RJ
初中数学
角的平分线
性质
判定
会综合利用性质和判定解决实际问题
角的平分线上的点到角的两边的距离相等
角的内部到角的两边的距离相等的点在角的平分线上
知识梳理
角的平分线
1.作已知角的平分线
(1)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
(2)分别以M,N为圆心,大于 MN
的长为半径画弧,两弧在∠AOB的内部
相交于点C.
C
B
N
O
M
A
(3)画射线OC,射线OC即为所求.
2.角的平分线的性质
角的平分线上的点到角的两边的距离相等.
几何表示:如图,∵OC是∠AOB的平分线,P是OC上一点,PD⊥OA,PE⊥OB,垂足分别为D,E.
∴PD=PE.
3.证明几何命题的一般步骤
(1)明确一个命题中的已知和求证;
(2)根据题意,画出图形,并用符号表示已知和求证;
(3)经过分析,找出由已知推出要证明的结论的途径,写出证明的过程.
4.角的平分线的判定
角的内部到角的两边的距离相等的点在角的平分线上.
几何表示:如图,∵点P是∠AOB内的一点,PD⊥OA,PE⊥OB,垂足分别为D,E,且PD=PE.
∴点P在∠AOB的平分线OC上.
1.如图,在△ABC中,AD是它的角平分线,P是AD一上点,
PE//AB,PF//AC,求证:点D到PE和PF的距离相等.
证明:∵PE//AB, ∴∠BAD=∠EPD.
∵PF//AC, ∴∠CAD=∠FPD.
∵AD是△ABC的角平分线,
∴∠BAD=∠CAD.
∴ ∠EPD=∠FPD,即PD平分∠EPF.
∴点D到PE和PF的距离相等.
C
A
E
F
D
P
B
重难剖析
2.如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA,PE⊥OB,垂足分别为点D,E,F是OC上的另一点,连接DF,EF.求证:DF=EF.
┐
O
B
A
C
P
E
D
┐
F
证明:∵OC是∠AOB的平分线,P是OC上一点,PD⊥OA,PE⊥OB.
∴∠POD=∠POE,DP=EP.
∴∠DPF=∠POD+∠ODP,∠EPF=∠POE+∠OEP.
∴∠DPF=∠EPF.
在△DPF和△EPF中,
DP=EP,
∠DPF=∠EPF,
PF=PF,
∴△DPF≌△EPF(SAS). ∴DF=EF.
┐
O
B
A
C
P
E
D
┐
F
3.证明:如果两个三角形有两条边和其中一条边上的中线分别相等,那么这两个三角形全等.
已知:如图,在△ABC和△DEF中,AC=DF,BC=EF,AM,DN分别为△ABC和△DEF的中线,且AM=DN.
求证:△ABC≌△DEF.
A
B
C
D
E
F
M
N
证明:∵BC=EF,AM,DN分别为△ABC和△DEF的中线, ∴CM=FN.
∵在△ACM和△DFN中, AM=DN,
AC=DF,
CM=FN,
∴△ACM≌△DFN. ∴∠C=∠F.
A
B
C
D
E
F
M
N
∵在△ABC和△DEF中, AC=DF,
∠C=∠F,
BC=EF,
∴△ABC≌△DEF.
A
B
C
D
E
F
M
N
4.如图,在△ABC中,AD是它的角平分线.求证:S△ABD:S△ACD=AB: AC.
证明:过点D作DE⊥AB,DF⊥AC,
垂足分别为E,F.
∵AD是△ABC的角平分线,∴DE=DF.
又∵S△ABD= AB DE,S△ACD= AC DF,
∴S△ABD:S△ACD=AB:AC.
A
B
C
D
E
F
┐
┐
1.如图,在四边形ABCD中,∠B=90°,AB//CD,M是BC的中点,AM平分∠DAB.
(1)DM是否平分∠ADC?请证明你的结论.
(2)线段DM与AM有怎样的位置关系?
请说明理由.
能力提升
判断两条线段的位置关系时,一般不是平行就是垂直,可先从这两种情况思考
E
解:(1)DM平分∠ADC. 证明如下:
如图,过点M作ME⊥AD,垂足为E.
∵∠B=90°,∴MB⊥AB.
∵AM平分∠DAB,MB⊥AB,ME⊥AD,
∴MB=ME. ∵∠B=90°,AB//CD.
∴∠C=90°,即MC⊥CD.
∵M为BC的中点, ∴MC=MB. ∴ME=MC.
∴DM平分∠ADC.
┐
E
(2)DM⊥AM. 理由如下:
∵AB//CD,∴∠CDA+∠BAD=180°.
又∵∠EDM=∠CDM= ∠CDA,
∠EAM=∠BAM= ∠BAD,
∴∠MDA+∠MAD= (∠CDA+∠BAD)=90°.
∴∠DMA=90°. ∴DM⊥AM.
┐
2.如图(1),在△ABC中,点D在边BC上,DE⊥AB,DF⊥AC,垂足分别为E,F,请你添加一个条件使得AD⊥EF.
(1)你添加的条件是 ,并证明AD⊥EF.
注意答案不唯一,可多思考几种答案
解:(1)AD平分∠BAC(答案不唯一),证明如下:
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF.
在Rt△ADE和Rt△ADF中, AD=AD,
DE=DF,
∴Rt△ADE≌Rt△ADF(HL).
∴∠EDA=∠FDA.
设AD交EF于点O,
在△DOE和△DOF中, DE=DF,
∠EDO=∠FDO,
DO=DO,
∴△DOE≌△DOF. ∴∠DOE=∠DOF.
∵∠DOE+∠DOF=180°.
∴∠DOE=∠DOF=90°,即AD⊥EF.
(2)如图(2),AD为∠BAC的平分线,当有一点G从点D向点A运动时,GE⊥AB,GF⊥AC,垂足分别为E,F.这时AD是否垂直于EF?
(3)如图(3),当点G从点D出发沿着AD方向运动时,其他条件同(2),这时AD是否垂直于EF?
(2)AD⊥EF,证明方法同(1).
(3)AD⊥EF,证明方法同(1).
由本题可以得出一般结论:从角平分线上一点向角两边引垂线,垂足的连线被角平分线垂直平分.
3.如图,点C在线段AB上,AD//EB,AC=BE,AD=BC
CF平分∠DCE.试探索CF和DE的位置关系,并说明理由.
解:CF⊥DE,证明如下:
∵AD//EB, ∴∠A=∠B.
在△ACD和△BEC中, AD=BC,
∠A=∠B,
AC=BE,
∴△ACD≌△BEC(SAS). ∴CD=EC.
A
B
C
D
E
F
∵CF平分∠DCE,∴∠DCF=∠ECF.
在△DCF和△ECF中, CD=CE,
∠DCF=∠ECF,
CF=CF,
∴△DCF≌△ECF(SAS).
∴∠CFD=∠CFE.
∵∠CFD+∠CFE=180°,
∴∠CFD=∠CFE=90°.
∴CF⊥DE.
A
B
C
D
E
F
