一元二次方程的复习课[上学期]
文档属性
| 名称 | 一元二次方程的复习课[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 338.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-12-27 09:30:00 | ||
图片预览








文档简介
课件26张PPT。一元二次方程
(复习课1)一元二次方程一般形式解法根的判别式:根与系数的关系:应用配方法求最值问题
实际应用思想方法转化思想; 配方法、换元法直接开平方法配方法公式法因式分解法ax2+bx+c=0(a≠0)知识结构定义及一般形式:只含有 一个 未知数,且未知数的最高次数为2 的 整式 方程叫做一元二次方程.
一元二次方程的一般形式是 ax2+bx+c=0 (a≠0);其中a是 二次项系数,b是一次项系数 ,c是 常数项.1、判断下面哪些方程是一元二次方程
√ √ × × × × 2、把方程(1-x)(2-x)=3-x2 化为一般形式是:___________, 其二次项系数是____,一次项系数是____,常数项是____.
3、方程(m-2)x|m| +3mx-4=0是关于x的一元二次方程,则 ( )
A.m=±2 B.m=2 C.m=-2 D.m≠ ±2
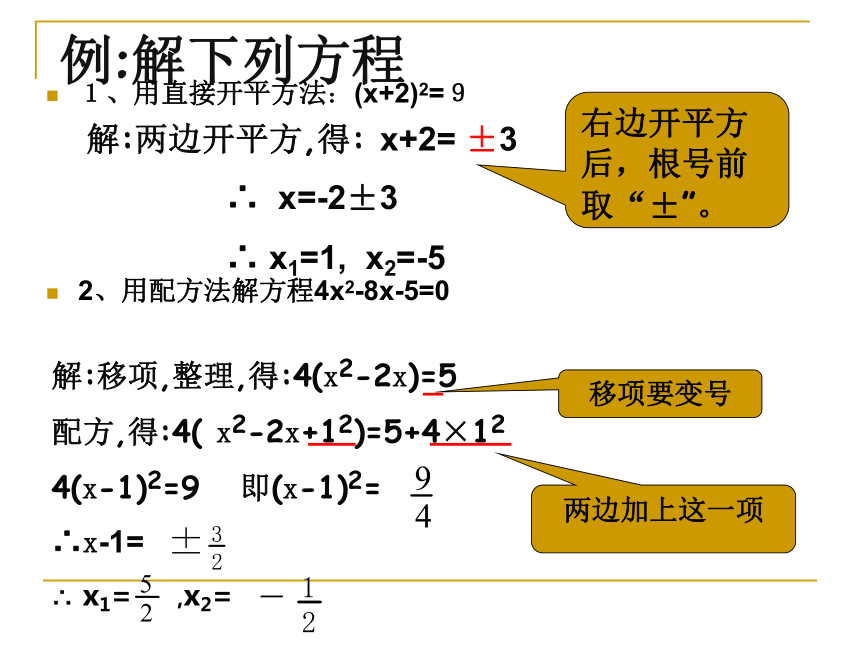
2x2-3x-1=02-3-1C(1)直接开平方法(2)配方法(3)公式法(4)因式分解法解一元二次方程的方法有几种? 例:解下列方程1、用直接开平方法:(x+2)2=9
2、用配方法解方程4x2-8x-5=0
解:两边开平方,得: x+2= ±3
∴ x=-2±3
∴ x1=1, x2=-5解:移项,整理,得:4(x2-2x)=5
配方,得:4( x2-2x+12)=5+4×12
4(x-1)2=9 即(x-1)2=
∴x-1=
∴ x1= ,x2=右边开平方后,根号前取“±”。
移项要变号两边加上这一项 解:移项,得: 3x2-4x-7=0 a=3 b=-4 c=-7 ∵b2-4ac=(-4)2-4×3×(-7)=100>0 ∴ ∴x1= x2 = 解:原方程化为 (y+2) 2﹣3(y+2)=0
(y+2)(y+2-3)=0
(y+2)(y-1)=0
y+2=0 或 y-1=0
∴y1=-2 y2=1先变为一般形式,代入时注意符号。 把y+2看作一个未知数,变成
(ax+b)(cx+d)=0形式。 3、用公式法解方程 3x2=4x+74、用分解因式法解方程:(y+2)2=3(y+2)-1实例讲解解: 注:常数项绝对值较大不宜分解因式,也不易用公式法求解,却易配方,从而用配方法。实例讲解解: 注:可见,化简繁,但左边两式形式相似,故考虑换元。配方法步骤:
① 二次项系数化为1;
②移项;
③两边加上一次项系数一半的平方;
④直接开平方。
公式法步骤:
① 先化为一般形式;
②确定a、b、c,求b2-4ac;
③ 当 b2-4ac≥ 0时,代入公式:
若b2-4ac<0,方程没有实数根。
分解因式法步骤:
①右边化为0,左边化成两个因式的积;
②分别令两个因式为0,求解。步骤归纳用配方法证明:
例1.关于x的方程(2m2 -12m +37)x 2 +3mx+1=0,无论m取何值,此方程都是一元二次方程例2.代数式2x2-8x+9何时能取得最小值,最小值是多少?配方法的应用1. (2005福州中考)
解方程: (x+1)(x+2)=6
2. (2005北京中考)
已知: (a2+b2)(a2+b2-3)=10
求a2+b2 的值。
3. (2004武汉中考)
试证明关于x的方程 (a2-a+2)x2+ax+2=0无论a取何值,该方程都是一元二次方程.中考直击思考练一练:1、对于任意实数x,多项式x2-5x+7的值是 ( )
A.负数 B.非正数 C.正数 D.无法确定正负的数
2、m为何值时,代数式3(m-2)2-1的值比2m+1的值大2?
3、已知2x2+5xy-7y2=0,且y≠0,求x∶y。 C练一练:1、若 (x+ )2 = ,试用配方法求(x- ) 2 的值。
2、 已知等腰三角形的底边长为8,腰长是方程x2-9x+20=0的一个根,求等腰三角形的周长。
4、解方程:x2-5∣x∣-6=0拓展练习:请同学们认真阅读下面的一段文字材料,然后解答题目中提出的有关问题.
为解方程(x2-1)2-5(x2-1)+4=0,我们可以将x2-1视为一个整体,然后设x2-1=y,则原方程可化为y2-5y+4=0 ①
解得y1=1,y2=4.
当y=1时,x2-1=1,∴x2=2,x=± .当y=4时,x2-1=4,∴x2=5,x=± . ∴原方程的解为x1= ,x2=- ,x3= ,x4=- .解答问题:
(1)填空:在由原方程得到方程①的过程中,利用_________法达到了降次的目的,体现了_________的数学思想.
(2)解方程x4-x2-6=0课堂小结:一元二次方程有三个特征:
(1)只含有一个未知数;
(2)未知数的最高次数为2;
(3)是整式方程。
如果方程ax2+bx+c=0是一元二次方程,那么a≠0.
解一元二次方程时应注意方程的特征,选择恰当的方法.一元二次方程
(复习课2)复习:一元二次方程 ax2+bx+c=0 (a≠0)根的情况是由⊿=b2-4ac的值决定的;
当⊿>0时,方程有两个不相等的实数根;
当⊿=0时,方程有两个相等的实数根;
(当⊿≥0时,方程有两个实数根.)
当⊿<0时,方程没有实数根;练习1:1、不解方程判别根的情况 :
(1)2x2-4x+1=0;
(2) 4y(y-5)+25=0;
(3)(x-4)(x+3)+14=0;
(4)(k2+1)x2-2kx+(k2+4)=0. 练习2:1、方程2x2+3x-k=0根的判别式是 ;当k 时,方程有实根。
2、方程x2+2x+m=0有两个相等实数根,则m= 。
3、当m 时,关于x的方程3x2-2(3m+1)x+3m2-1=0有两个不相等的实数根。
4、关于x的一元二次方程mx2+(2m-1)x-2=0的根的判别式的值等于4,则m= 。 一元二次方程的根与系数的关系:如果方程ax2+bx+c=0(a≠0)的两个根是X1 , X2 ,那么X1+x2= , X1x2= -(韦达定理)注:能用根与系数的关系的
前提条件为b2-4ac≥0.例题分析:【例1】 关于x的方程2x2+kx-4=0的一个根是-2,则方程的另一根是 ;k= 。
【例2】x1,x2是方程2x2-3x-5=0的两个根,不解方程,求下列代数式的值:
(1)x12+x22
(2)︱x1-x2︱
(3)x12+3x22-3x2 练习3:1、已知x1、x2是方程2x2+3x-4=0的两个根,那么:x1+x2= ; = ; x12+x22= .
2、以2和3为根的一元二次方程(二次项系数为1)是 .
3、若α、β为实数且|α+β-3|+(2-αβ)2=0, 则以α、β为根的一元二次方程 是 . 例题分析:【例3】已知关于x的二次方程x2-2(a-2)x+a2-5=0有实数根,且两根之积等于两根之和的2倍,求a的值。
【例4】已知x1,x2是关于x的方程x2+px+q=0的两根,x1+1,x2+1是关于x的方程x2+qx+p=0的两根,求常数p、q的值。 拓展练习:1、当a,c异号时,一元二次方程ax2+bx+c=0的根的情况是 ( )
A.有两个相等的实数根 B. 有两个不相等的实数根
C. 没有实数根 D.不能确定
2、如果关于x的一元二次方程2x(ax-4)-x2+6=0没有实数根,那么a的最小整数值是 。
3、已知关于x的方程x2-2x-m=0无实根(m为实数),证明关于x的方程x2+2mx+1+2(m2-1)(x2+1)=0也无实根。
B2
(复习课1)一元二次方程一般形式解法根的判别式:根与系数的关系:应用配方法求最值问题
实际应用思想方法转化思想; 配方法、换元法直接开平方法配方法公式法因式分解法ax2+bx+c=0(a≠0)知识结构定义及一般形式:只含有 一个 未知数,且未知数的最高次数为2 的 整式 方程叫做一元二次方程.
一元二次方程的一般形式是 ax2+bx+c=0 (a≠0);其中a是 二次项系数,b是一次项系数 ,c是 常数项.1、判断下面哪些方程是一元二次方程
√ √ × × × × 2、把方程(1-x)(2-x)=3-x2 化为一般形式是:___________, 其二次项系数是____,一次项系数是____,常数项是____.
3、方程(m-2)x|m| +3mx-4=0是关于x的一元二次方程,则 ( )
A.m=±2 B.m=2 C.m=-2 D.m≠ ±2
2x2-3x-1=02-3-1C(1)直接开平方法(2)配方法(3)公式法(4)因式分解法解一元二次方程的方法有几种? 例:解下列方程1、用直接开平方法:(x+2)2=9
2、用配方法解方程4x2-8x-5=0
解:两边开平方,得: x+2= ±3
∴ x=-2±3
∴ x1=1, x2=-5解:移项,整理,得:4(x2-2x)=5
配方,得:4( x2-2x+12)=5+4×12
4(x-1)2=9 即(x-1)2=
∴x-1=
∴ x1= ,x2=右边开平方后,根号前取“±”。
移项要变号两边加上这一项 解:移项,得: 3x2-4x-7=0 a=3 b=-4 c=-7 ∵b2-4ac=(-4)2-4×3×(-7)=100>0 ∴ ∴x1= x2 = 解:原方程化为 (y+2) 2﹣3(y+2)=0
(y+2)(y+2-3)=0
(y+2)(y-1)=0
y+2=0 或 y-1=0
∴y1=-2 y2=1先变为一般形式,代入时注意符号。 把y+2看作一个未知数,变成
(ax+b)(cx+d)=0形式。 3、用公式法解方程 3x2=4x+74、用分解因式法解方程:(y+2)2=3(y+2)-1实例讲解解: 注:常数项绝对值较大不宜分解因式,也不易用公式法求解,却易配方,从而用配方法。实例讲解解: 注:可见,化简繁,但左边两式形式相似,故考虑换元。配方法步骤:
① 二次项系数化为1;
②移项;
③两边加上一次项系数一半的平方;
④直接开平方。
公式法步骤:
① 先化为一般形式;
②确定a、b、c,求b2-4ac;
③ 当 b2-4ac≥ 0时,代入公式:
若b2-4ac<0,方程没有实数根。
分解因式法步骤:
①右边化为0,左边化成两个因式的积;
②分别令两个因式为0,求解。步骤归纳用配方法证明:
例1.关于x的方程(2m2 -12m +37)x 2 +3mx+1=0,无论m取何值,此方程都是一元二次方程例2.代数式2x2-8x+9何时能取得最小值,最小值是多少?配方法的应用1. (2005福州中考)
解方程: (x+1)(x+2)=6
2. (2005北京中考)
已知: (a2+b2)(a2+b2-3)=10
求a2+b2 的值。
3. (2004武汉中考)
试证明关于x的方程 (a2-a+2)x2+ax+2=0无论a取何值,该方程都是一元二次方程.中考直击思考练一练:1、对于任意实数x,多项式x2-5x+7的值是 ( )
A.负数 B.非正数 C.正数 D.无法确定正负的数
2、m为何值时,代数式3(m-2)2-1的值比2m+1的值大2?
3、已知2x2+5xy-7y2=0,且y≠0,求x∶y。 C练一练:1、若 (x+ )2 = ,试用配方法求(x- ) 2 的值。
2、 已知等腰三角形的底边长为8,腰长是方程x2-9x+20=0的一个根,求等腰三角形的周长。
4、解方程:x2-5∣x∣-6=0拓展练习:请同学们认真阅读下面的一段文字材料,然后解答题目中提出的有关问题.
为解方程(x2-1)2-5(x2-1)+4=0,我们可以将x2-1视为一个整体,然后设x2-1=y,则原方程可化为y2-5y+4=0 ①
解得y1=1,y2=4.
当y=1时,x2-1=1,∴x2=2,x=± .当y=4时,x2-1=4,∴x2=5,x=± . ∴原方程的解为x1= ,x2=- ,x3= ,x4=- .解答问题:
(1)填空:在由原方程得到方程①的过程中,利用_________法达到了降次的目的,体现了_________的数学思想.
(2)解方程x4-x2-6=0课堂小结:一元二次方程有三个特征:
(1)只含有一个未知数;
(2)未知数的最高次数为2;
(3)是整式方程。
如果方程ax2+bx+c=0是一元二次方程,那么a≠0.
解一元二次方程时应注意方程的特征,选择恰当的方法.一元二次方程
(复习课2)复习:一元二次方程 ax2+bx+c=0 (a≠0)根的情况是由⊿=b2-4ac的值决定的;
当⊿>0时,方程有两个不相等的实数根;
当⊿=0时,方程有两个相等的实数根;
(当⊿≥0时,方程有两个实数根.)
当⊿<0时,方程没有实数根;练习1:1、不解方程判别根的情况 :
(1)2x2-4x+1=0;
(2) 4y(y-5)+25=0;
(3)(x-4)(x+3)+14=0;
(4)(k2+1)x2-2kx+(k2+4)=0. 练习2:1、方程2x2+3x-k=0根的判别式是 ;当k 时,方程有实根。
2、方程x2+2x+m=0有两个相等实数根,则m= 。
3、当m 时,关于x的方程3x2-2(3m+1)x+3m2-1=0有两个不相等的实数根。
4、关于x的一元二次方程mx2+(2m-1)x-2=0的根的判别式的值等于4,则m= 。 一元二次方程的根与系数的关系:如果方程ax2+bx+c=0(a≠0)的两个根是X1 , X2 ,那么X1+x2= , X1x2= -(韦达定理)注:能用根与系数的关系的
前提条件为b2-4ac≥0.例题分析:【例1】 关于x的方程2x2+kx-4=0的一个根是-2,则方程的另一根是 ;k= 。
【例2】x1,x2是方程2x2-3x-5=0的两个根,不解方程,求下列代数式的值:
(1)x12+x22
(2)︱x1-x2︱
(3)x12+3x22-3x2 练习3:1、已知x1、x2是方程2x2+3x-4=0的两个根,那么:x1+x2= ; = ; x12+x22= .
2、以2和3为根的一元二次方程(二次项系数为1)是 .
3、若α、β为实数且|α+β-3|+(2-αβ)2=0, 则以α、β为根的一元二次方程 是 . 例题分析:【例3】已知关于x的二次方程x2-2(a-2)x+a2-5=0有实数根,且两根之积等于两根之和的2倍,求a的值。
【例4】已知x1,x2是关于x的方程x2+px+q=0的两根,x1+1,x2+1是关于x的方程x2+qx+p=0的两根,求常数p、q的值。 拓展练习:1、当a,c异号时,一元二次方程ax2+bx+c=0的根的情况是 ( )
A.有两个相等的实数根 B. 有两个不相等的实数根
C. 没有实数根 D.不能确定
2、如果关于x的一元二次方程2x(ax-4)-x2+6=0没有实数根,那么a的最小整数值是 。
3、已知关于x的方程x2-2x-m=0无实根(m为实数),证明关于x的方程x2+2mx+1+2(m2-1)(x2+1)=0也无实根。
B2
同课章节目录
