鲁教版(五四制)数学八年级上册 3.3 三角形的中位线(1)课件(共20张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学八年级上册 3.3 三角形的中位线(1)课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 474.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-04 16:05:01 | ||
图片预览




文档简介
(共20张PPT)
第一课时
三角形的中位线
Contents
目录
01
02
03
04
问题引入
课堂小结
合作探究
拓展练习
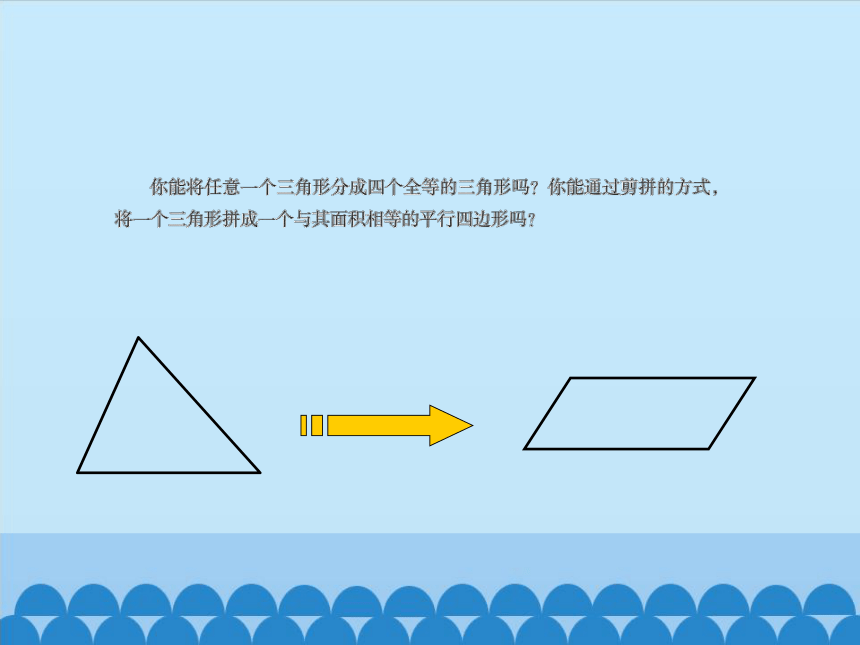
剪一刀,将一张三角形纸片剪成一张三角形纸片和一张梯形纸片。
(1)如果要求剪得的两张纸片能拼成平行四边形,剪痕的位置有什么要求?
(2)要把所剪得的两个图形拼成一个平行四边形,可将其中的三角形作怎样的图形变换?
动画演示
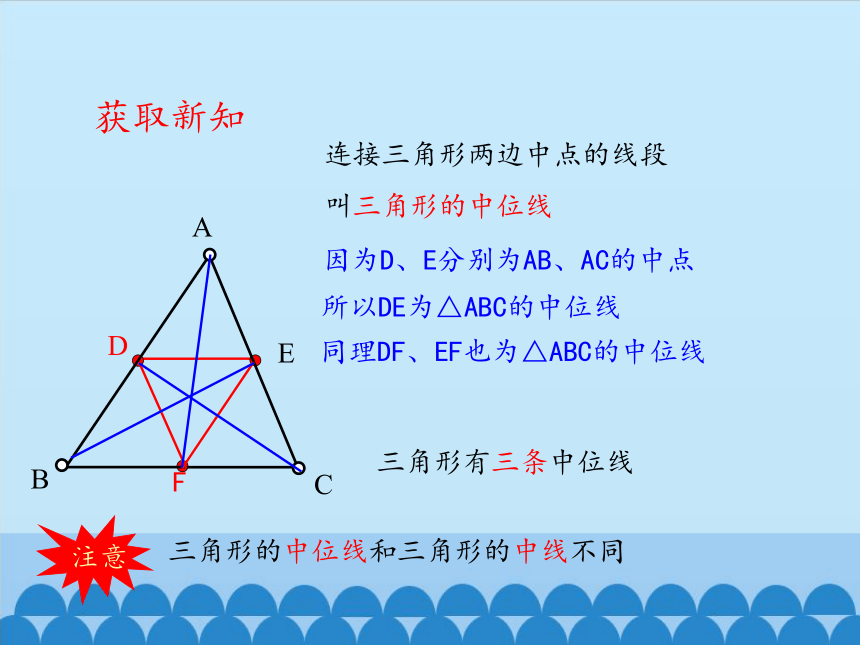
连接三角形两边中点的线段
叫三角形的中位线
三角形有三条中位线
因为D、E分别为AB、AC的中点
三角形的中位线和三角形的中线不同
同理DF、EF也为△ABC的中位线
E
D
F
A
C
B
所以DE为△ABC的中位线
注意
获取新知
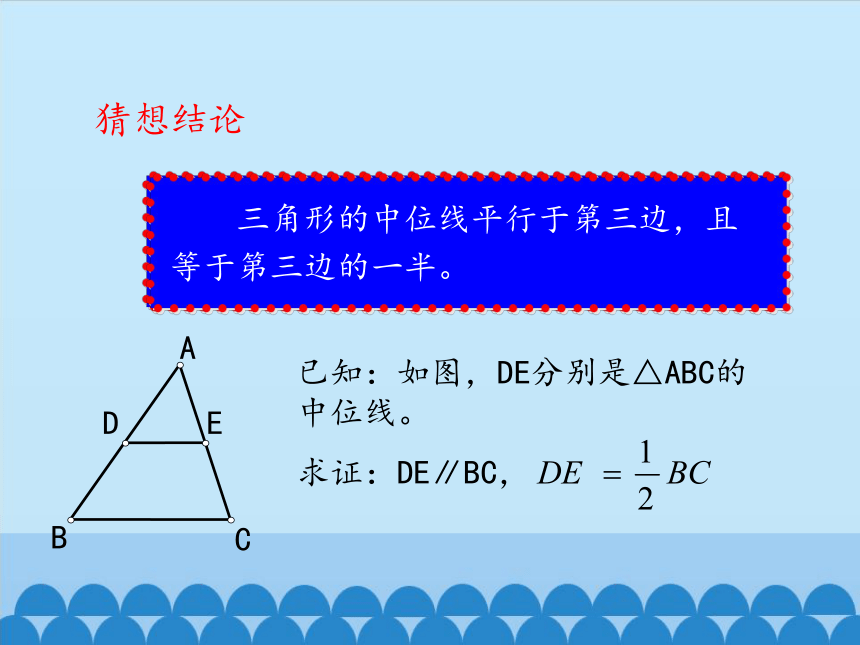
已知:如图,DE分别是△ABC的中位线。
求证:DE∥BC,
C
E
D
B
A
温馨提示:与第三边的位置关系?与第三边的数量关系?
三角形的中位线平行于第三边,且等于第三边的一半。
猜想结论
C
E
D
F
B
A
你还能用不同的方法加以证明吗
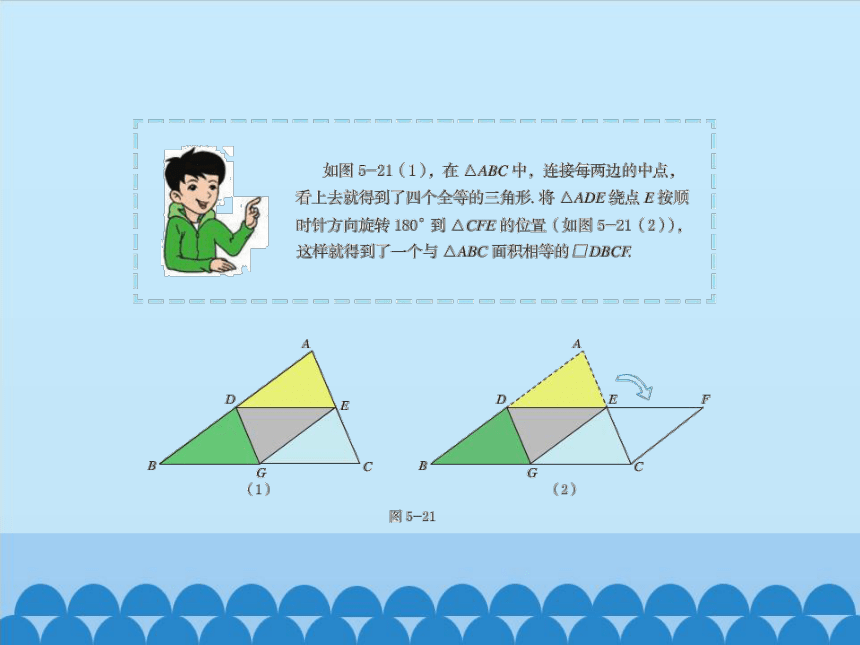
证明:如图,以点E为旋转中心,把△ADE绕点E,按顺时针方向旋转180゜,得到△ CFE,则D,E,F同在一直线上DE=EF,且△ADE≌△CFE。
∴∠ADE=∠F,AD=CF,
∴AB∥CF。
又∵BD=AD=CF,
∴四边形BCFD是平行四边形(一组对边平行且相等的四边形是平行四边形)。
∴DF∥BC(根据什么?)
方法1
C
E
D
F
A
方法2
B
A
B
C
D
E
方法3
方法4
F
B
C
E
D
A
三角形的中位线性质
如果DE是△ABC的中位线
那么⑴ DE∥BC,
⑵ DE=1/2BC
① 证明平行问题
② 证明一条线段是另一条线段的2倍或1/2
用 途
A
B
C
D
E
由中点想到
中线、中位线
三角形的中位线平行于第三边,并且等于第三边的一半。
如图,任意画一个四边形ABCD,并将四边的中点E、F、G、H依次连接起来,得到一个新四边形EFGH,四边形EFGH的形状有什么特征?请证明你的结论,并与同伴交流。
A
B
C
D
E
F
G
H
分析:由E、F、G、H分别是四边形ABCD各边的中点,联想到应用三角形的中位线定理来证明。
定义:连接三角形两边中点的线段叫做三角形的中位线。
性质:三角形的中位线平行于第三边, 并且等于第三边的一半。
作业布置
课本习题5.7 技能 1、2 数学理解 3
谢 谢
第一课时
三角形的中位线
Contents
目录
01
02
03
04
问题引入
课堂小结
合作探究
拓展练习
剪一刀,将一张三角形纸片剪成一张三角形纸片和一张梯形纸片。
(1)如果要求剪得的两张纸片能拼成平行四边形,剪痕的位置有什么要求?
(2)要把所剪得的两个图形拼成一个平行四边形,可将其中的三角形作怎样的图形变换?
动画演示
连接三角形两边中点的线段
叫三角形的中位线
三角形有三条中位线
因为D、E分别为AB、AC的中点
三角形的中位线和三角形的中线不同
同理DF、EF也为△ABC的中位线
E
D
F
A
C
B
所以DE为△ABC的中位线
注意
获取新知
已知:如图,DE分别是△ABC的中位线。
求证:DE∥BC,
C
E
D
B
A
温馨提示:与第三边的位置关系?与第三边的数量关系?
三角形的中位线平行于第三边,且等于第三边的一半。
猜想结论
C
E
D
F
B
A
你还能用不同的方法加以证明吗
证明:如图,以点E为旋转中心,把△ADE绕点E,按顺时针方向旋转180゜,得到△ CFE,则D,E,F同在一直线上DE=EF,且△ADE≌△CFE。
∴∠ADE=∠F,AD=CF,
∴AB∥CF。
又∵BD=AD=CF,
∴四边形BCFD是平行四边形(一组对边平行且相等的四边形是平行四边形)。
∴DF∥BC(根据什么?)
方法1
C
E
D
F
A
方法2
B
A
B
C
D
E
方法3
方法4
F
B
C
E
D
A
三角形的中位线性质
如果DE是△ABC的中位线
那么⑴ DE∥BC,
⑵ DE=1/2BC
① 证明平行问题
② 证明一条线段是另一条线段的2倍或1/2
用 途
A
B
C
D
E
由中点想到
中线、中位线
三角形的中位线平行于第三边,并且等于第三边的一半。
如图,任意画一个四边形ABCD,并将四边的中点E、F、G、H依次连接起来,得到一个新四边形EFGH,四边形EFGH的形状有什么特征?请证明你的结论,并与同伴交流。
A
B
C
D
E
F
G
H
分析:由E、F、G、H分别是四边形ABCD各边的中点,联想到应用三角形的中位线定理来证明。
定义:连接三角形两边中点的线段叫做三角形的中位线。
性质:三角形的中位线平行于第三边, 并且等于第三边的一半。
作业布置
课本习题5.7 技能 1、2 数学理解 3
谢 谢
