冀教版数学八年级上册12.1分式 课件(共25张PPT)
文档属性
| 名称 | 冀教版数学八年级上册12.1分式 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-04 15:52:02 | ||
图片预览








文档简介
(共25张PPT)
分式
1.一项工程,甲施工队5天可以完成.甲施工队每天完成的工作量是多少?3天完成的工作量又是多少?如果乙施工队a天可以完成这项工程,那么乙施工队每天完成的工作量是多少?b(b解:设这项工程的总工作量为1.
则甲施工队5天完成时的工作量是 .
3天完成的工作量是 .
如果乙施工队a天完成,则乙队每天完成工作量为 .
b天完成的工作量为 .
解:A车的速度为n km/h,根据
时间 =
得A车所用时间为t= h.
B车速度为(n+20) km/h.
所以B车所用时间为t= .
2.已知甲、乙两地之间的路程为m km.如果A车的速度为n km/h,B车比A车每小时多行20km,那么从甲地到乙地,A车和B车所用的时间各为多少?
分式定义:一般的,我们把形如 的代数式叫做分式,其中,A,B都是整式,且B中含有字母.
A叫做分式的分子,B叫做分式的分母.
①分子分母都是整式
②分母中含有字母
分式的概念
③分母不能为零
分母中含有字母的是分式
分母中不含字母的是整式
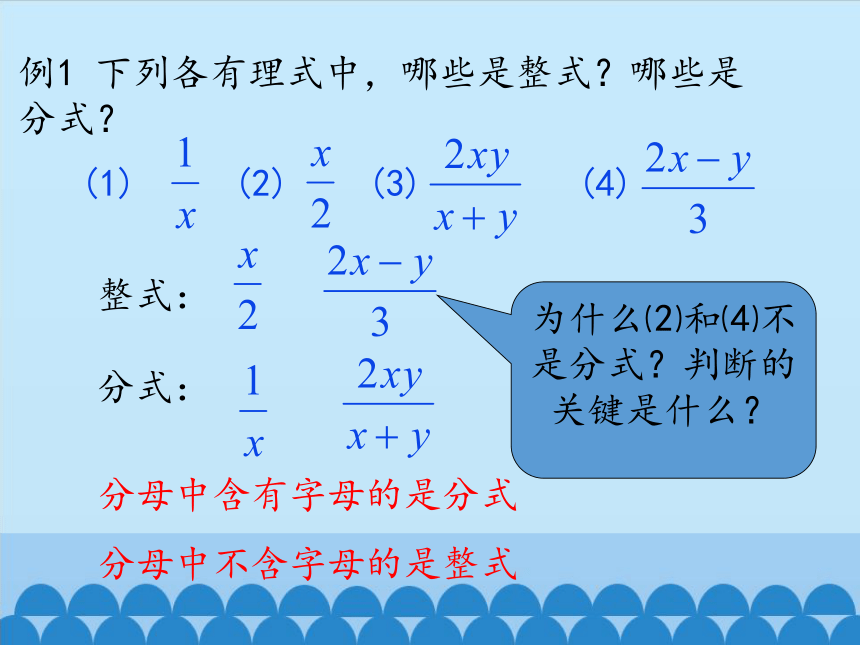
例1 下列各有理式中,哪些是整式?哪些是分式?
(1) (2) (3) (4)
整式:
分式:
为什么⑵和⑷不是分式?判断的关键是什么?
1.下列各式中,哪些是整式?哪些是分式?
(1)5x-7 (2) (3)3x2-1
(4) (5)
(6) (7)
(8)
整式:
分式:
⑴⑵⑶⑻
⑷⑸⑹⑺
巩固练习
做一做:
分式 与 相等吗?还有与它们相等的分式吗?如果有,请你写出两个这样的分式.
答:有这样的分式.
例如:
练习:
1.当x取何值时,下列分式有意义?
(1) ; (2) .
解:当分母不为0时,分式有意义.
(1)x取除1以外的任意数,分式有意义;
(2)x取除 以外的任意数,分式有意义.
练习:
2.判断下面的语句是否正确,并说明理由.
(1)分式 与 相等.(2)分式 与 相等.
(3)分式 与 相等.(4)分式 与 相等.
√
√
√
×
分式的基本性质:分式的分子分母同时乘以或除以一个不等于0的整式,分式的值不变.
二、分式的求值
例:当a=1,2时,分别求分式 的值.
解:
当a=1时,
=
=1
当a=2时,
=
=
做一做
当p=12,q=-8时,请分别用直接代入求值和化简后代入求值两种方法求分式 的值,并比较那种方法较简单.
解:直接代入求值法:
将p=12,q=-8代入分式得,
当p=12,q=-8时,请分别用直接代入求值和化简后代入求值两种方法求分式 的值,并比较那种方法较简单.
做一做
解:先化简后代入求值:
将p=12,q=-8代入化简后的分式得,
先化简后代入求值比较简单.
三个条件
1.分式无意义的条件
2.分式有意义的条件
3.分式的值等于零的条件
分母等于零
分母不等于零
分子等于零且分母不等于零
例:对于分式 .
⑴当x等于何值时,分式无意义?
⑵当x等于何值时,分式的值为零?
解(1)由x-2=0,得x=2.
∴当x=2时,分式无意义.
解(2)由x -4=0,得x=2或-2;
由x-2≠0,得x≠2.
∴x=-2时,分式的值为零.
随堂练习
1.若分式 无意义,则x=______.
2.若分式 有意义,则x应取何值?
3.若分式 =0,则x=_______.
4.若分式 =0,则x=_______.
3或-3
任意实数
3
-3
分式
思考:
(1)当x____时, 有意义;
(2)当x____时, 是负数;
(3)当x____时, 的值为0;
(4)当x____时, 是正数
类比分数的基本性质,得到:
分式的基本性质:
分式的分子和分母同时乘(或除以)同一个不等于0的整式,分式的值不变.
例1 下列等式的右边是怎样从左边得到的?
(1)
为什么给出 ?
(2)
为什么本题未给 ?
由(2)知
解: 由(1)知
巩固练习
1.若把分式 的 和 都扩大两倍,则分式
的值( ).
A.扩大两倍 B.不变
C.缩小两倍 D.缩小四倍
2.若把分式 中的 和 都扩大3倍,
那么分式的值( ).
A.扩大3倍 B.扩大9倍
C.扩大4倍 D.不变
B
A
分数是如何约分的?
1、约分:
约去分子与分母的最大公约数,化为最简分数.
=
这一过程实际上是将分式中分子与分母的公因式约去.
把分式分子、分母的公因式约去,这种变形叫分式的约分.分子和分母没有公因式的分式叫做最简分式.
分式约分的依据是什么?
分式的基本性质
观察下列化简过程,你能发现什么?
解:
找公因式方法
(1)约去系数的最大公约数
(2)约去分子分母相同因式的最低次幂
{
例1:约分
例2:约分
分析:为约分要先找出分子和分母的公因式.
解:
约分时,分子或分母若是多项式,能分解则必须先进行因式分解.再找出分子和分母的公因式进行约分.
约分
(3)
(4)
练习
谢 谢
分式
1.一项工程,甲施工队5天可以完成.甲施工队每天完成的工作量是多少?3天完成的工作量又是多少?如果乙施工队a天可以完成这项工程,那么乙施工队每天完成的工作量是多少?b(b
则甲施工队5天完成时的工作量是 .
3天完成的工作量是 .
如果乙施工队a天完成,则乙队每天完成工作量为 .
b天完成的工作量为 .
解:A车的速度为n km/h,根据
时间 =
得A车所用时间为t= h.
B车速度为(n+20) km/h.
所以B车所用时间为t= .
2.已知甲、乙两地之间的路程为m km.如果A车的速度为n km/h,B车比A车每小时多行20km,那么从甲地到乙地,A车和B车所用的时间各为多少?
分式定义:一般的,我们把形如 的代数式叫做分式,其中,A,B都是整式,且B中含有字母.
A叫做分式的分子,B叫做分式的分母.
①分子分母都是整式
②分母中含有字母
分式的概念
③分母不能为零
分母中含有字母的是分式
分母中不含字母的是整式
例1 下列各有理式中,哪些是整式?哪些是分式?
(1) (2) (3) (4)
整式:
分式:
为什么⑵和⑷不是分式?判断的关键是什么?
1.下列各式中,哪些是整式?哪些是分式?
(1)5x-7 (2) (3)3x2-1
(4) (5)
(6) (7)
(8)
整式:
分式:
⑴⑵⑶⑻
⑷⑸⑹⑺
巩固练习
做一做:
分式 与 相等吗?还有与它们相等的分式吗?如果有,请你写出两个这样的分式.
答:有这样的分式.
例如:
练习:
1.当x取何值时,下列分式有意义?
(1) ; (2) .
解:当分母不为0时,分式有意义.
(1)x取除1以外的任意数,分式有意义;
(2)x取除 以外的任意数,分式有意义.
练习:
2.判断下面的语句是否正确,并说明理由.
(1)分式 与 相等.(2)分式 与 相等.
(3)分式 与 相等.(4)分式 与 相等.
√
√
√
×
分式的基本性质:分式的分子分母同时乘以或除以一个不等于0的整式,分式的值不变.
二、分式的求值
例:当a=1,2时,分别求分式 的值.
解:
当a=1时,
=
=1
当a=2时,
=
=
做一做
当p=12,q=-8时,请分别用直接代入求值和化简后代入求值两种方法求分式 的值,并比较那种方法较简单.
解:直接代入求值法:
将p=12,q=-8代入分式得,
当p=12,q=-8时,请分别用直接代入求值和化简后代入求值两种方法求分式 的值,并比较那种方法较简单.
做一做
解:先化简后代入求值:
将p=12,q=-8代入化简后的分式得,
先化简后代入求值比较简单.
三个条件
1.分式无意义的条件
2.分式有意义的条件
3.分式的值等于零的条件
分母等于零
分母不等于零
分子等于零且分母不等于零
例:对于分式 .
⑴当x等于何值时,分式无意义?
⑵当x等于何值时,分式的值为零?
解(1)由x-2=0,得x=2.
∴当x=2时,分式无意义.
解(2)由x -4=0,得x=2或-2;
由x-2≠0,得x≠2.
∴x=-2时,分式的值为零.
随堂练习
1.若分式 无意义,则x=______.
2.若分式 有意义,则x应取何值?
3.若分式 =0,则x=_______.
4.若分式 =0,则x=_______.
3或-3
任意实数
3
-3
分式
思考:
(1)当x____时, 有意义;
(2)当x____时, 是负数;
(3)当x____时, 的值为0;
(4)当x____时, 是正数
类比分数的基本性质,得到:
分式的基本性质:
分式的分子和分母同时乘(或除以)同一个不等于0的整式,分式的值不变.
例1 下列等式的右边是怎样从左边得到的?
(1)
为什么给出 ?
(2)
为什么本题未给 ?
由(2)知
解: 由(1)知
巩固练习
1.若把分式 的 和 都扩大两倍,则分式
的值( ).
A.扩大两倍 B.不变
C.缩小两倍 D.缩小四倍
2.若把分式 中的 和 都扩大3倍,
那么分式的值( ).
A.扩大3倍 B.扩大9倍
C.扩大4倍 D.不变
B
A
分数是如何约分的?
1、约分:
约去分子与分母的最大公约数,化为最简分数.
=
这一过程实际上是将分式中分子与分母的公因式约去.
把分式分子、分母的公因式约去,这种变形叫分式的约分.分子和分母没有公因式的分式叫做最简分式.
分式约分的依据是什么?
分式的基本性质
观察下列化简过程,你能发现什么?
解:
找公因式方法
(1)约去系数的最大公约数
(2)约去分子分母相同因式的最低次幂
{
例1:约分
例2:约分
分析:为约分要先找出分子和分母的公因式.
解:
约分时,分子或分母若是多项式,能分解则必须先进行因式分解.再找出分子和分母的公因式进行约分.
约分
(3)
(4)
练习
谢 谢
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
