冀教版数学八年级上册17.3勾股定理(1) 课件(共20张PPT)
文档属性
| 名称 | 冀教版数学八年级上册17.3勾股定理(1) 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-04 15:49:40 | ||
图片预览



文档简介
(共20张PPT)
毕达哥拉斯
B
我学习
观看视频,
记录毕达哥拉斯的发现.
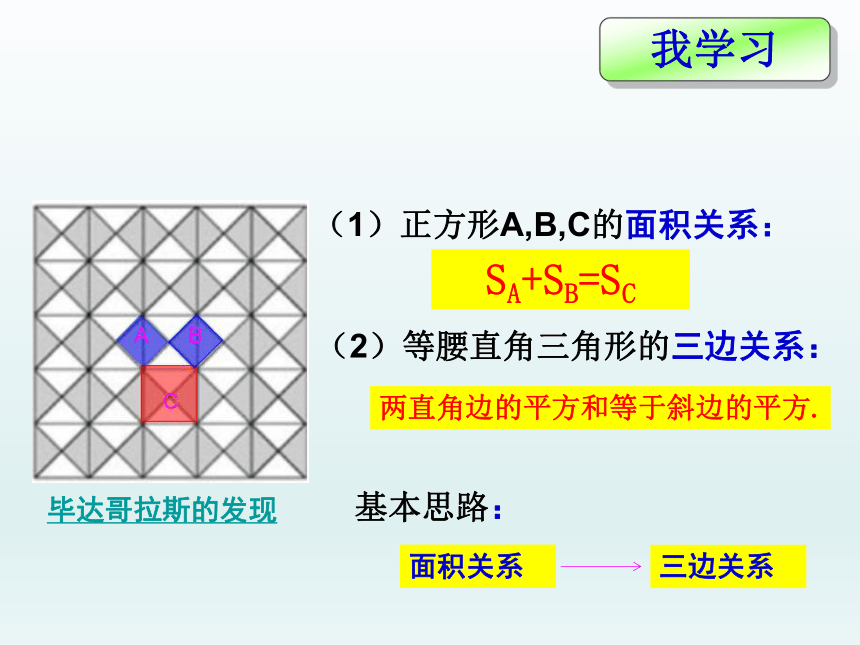
SA+SB=SC
(1)正方形A,B,C的面积关系:
(2)等腰直角三角形的三边关系:
两直角边的平方和等于斜边的平方.
面积关系
三边关系
基本思路:
我学习
毕达哥拉斯的发现
等腰直角三角形有上述性质,
其他的直角三角形是否也有类似的性质呢
我思考
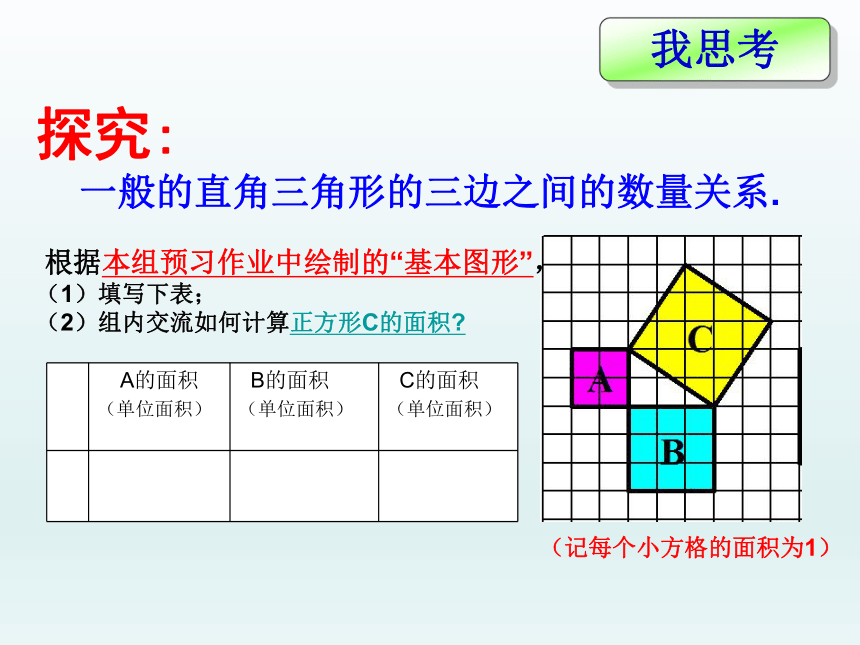
探究:
一般的直角三角形的三边之间的数量关系.
我思考
根据本组预习作业中绘制的“基本图形”,
(1)填写下表;
(2)组内交流如何计算正方形C的面积
A的面积
(单位面积) B的面积
(单位面积)
C的面积
(单位面积)
(记每个小方格的面积为1)
我猜想
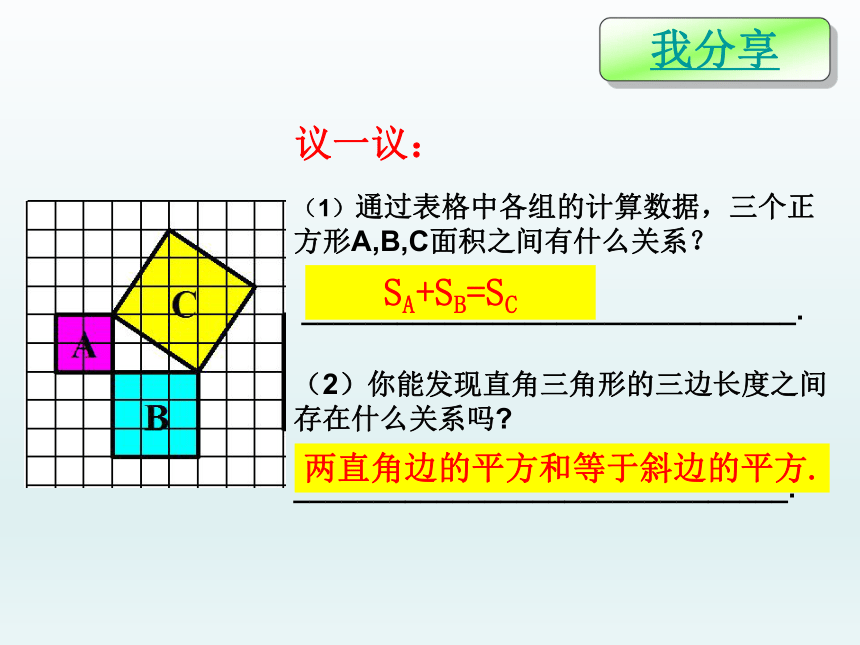
(1)通过表格中各组的计算数据,三个正
方形A,B,C面积之间有什么关系?
_______________________________.
(2)你能发现直角三角形的三边长度之间
存在什么关系吗
_______________________________.
我分享
SA+SB=SC
两直角边的平方和等于斜边的平方.
议一议:
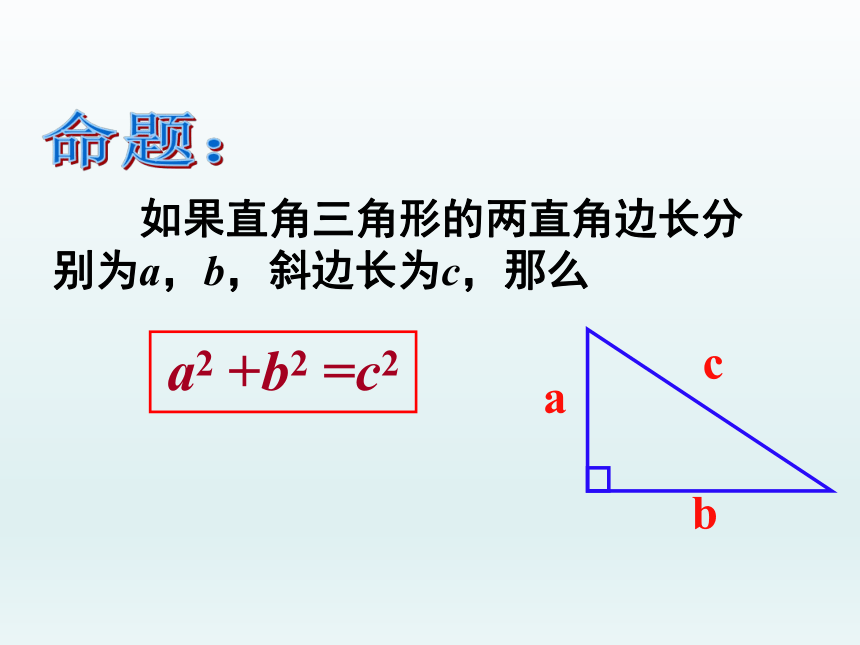
a2 +b2 =c2
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么
a
b
c
冀教版八年级(下)第十七章
长郡雨花外国语学校
初二数学组 李貌
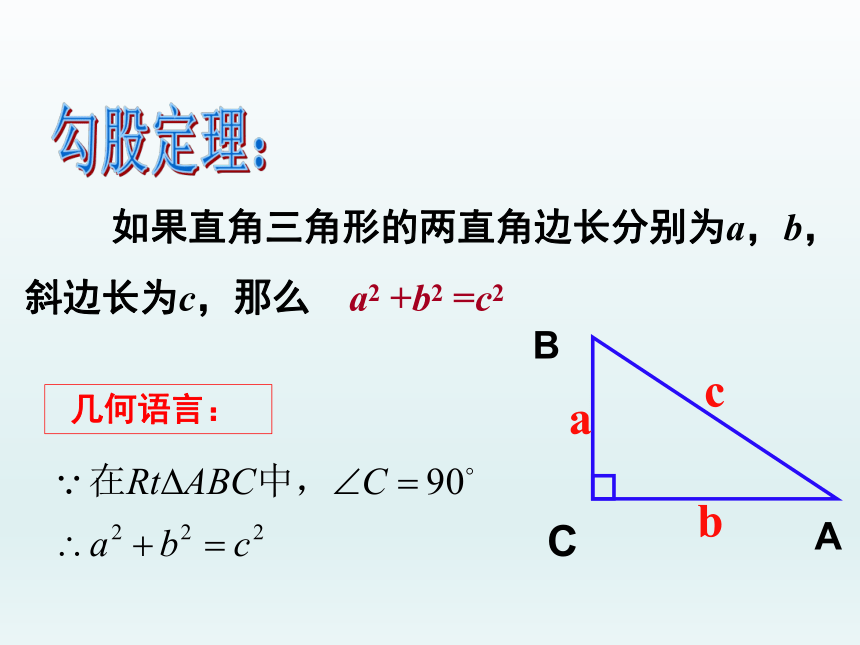
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么 a2 +b2 =c2
a
b
c
B
C
A
几何语言:
游戏规则:
听到“开始”口令时立即举手,根据举手速度最快或举手小组人数最多的同学抢得红包. 每个红包内有一个问题,答对即可获得分数!快来抢吧!
抢红包啦!!
抢红包啦!!
2分题
1分题
3分题
4分题
4分题
2分题
我能行
若a=3,b=4,则c=______;
如图,在Rt△ABC中,∠C=90°
a
b
c
A
C
B
5
相关知识链接:
3分题
我挑战
在Rt△ABC中,∠C=90°,若a=3,b=4,
则c=__________;
思考:若本题中,删去∠C=90°这一条件,答案是否发生变化?
在Rt△ABC中,若a=3,b=4, 则c =_______.
5
“分类讨论”
解题策略:
4分题
我突破
如图,是由四个全等的直角三角形适当拼接后形成的图形,这些直角三角形的两直角边分别为a、b,斜边为c,你能用这个图形验证勾股定理吗?
c
b
a
a2 +b2 = c2
这个图案被选为2002年在北京召开的国际数学家大会的会徽。
“赵爽弦图”
c
b
a
用赵爽弦图证明勾股定理
=
b
a
a
我了解
4分题
机会总是留给
有勇气、有准备的人!
直接得1分!!
1分题
我勇敢
4分题
我有感悟,我有收获…
我成功
解法的多元化
“殊途同归”
http://blog..cn/s/blog_a595144c0101f1a1.html
勾股定理的多种证明知识链接:
(a + b)(b + a) =
a2 +
a2 + b2 = c2
b
b
a
a
c
c
∟
∟
∟
c2
+ 2( )
+ ab
+ b2
=
c2
ab
ab
我展示
a2 + b2 = c2
a2
b2
a2
c2
我展示
谢谢指导!
毕达哥拉斯
B
我学习
观看视频,
记录毕达哥拉斯的发现.
SA+SB=SC
(1)正方形A,B,C的面积关系:
(2)等腰直角三角形的三边关系:
两直角边的平方和等于斜边的平方.
面积关系
三边关系
基本思路:
我学习
毕达哥拉斯的发现
等腰直角三角形有上述性质,
其他的直角三角形是否也有类似的性质呢
我思考
探究:
一般的直角三角形的三边之间的数量关系.
我思考
根据本组预习作业中绘制的“基本图形”,
(1)填写下表;
(2)组内交流如何计算正方形C的面积
A的面积
(单位面积) B的面积
(单位面积)
C的面积
(单位面积)
(记每个小方格的面积为1)
我猜想
(1)通过表格中各组的计算数据,三个正
方形A,B,C面积之间有什么关系?
_______________________________.
(2)你能发现直角三角形的三边长度之间
存在什么关系吗
_______________________________.
我分享
SA+SB=SC
两直角边的平方和等于斜边的平方.
议一议:
a2 +b2 =c2
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么
a
b
c
冀教版八年级(下)第十七章
长郡雨花外国语学校
初二数学组 李貌
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么 a2 +b2 =c2
a
b
c
B
C
A
几何语言:
游戏规则:
听到“开始”口令时立即举手,根据举手速度最快或举手小组人数最多的同学抢得红包. 每个红包内有一个问题,答对即可获得分数!快来抢吧!
抢红包啦!!
抢红包啦!!
2分题
1分题
3分题
4分题
4分题
2分题
我能行
若a=3,b=4,则c=______;
如图,在Rt△ABC中,∠C=90°
a
b
c
A
C
B
5
相关知识链接:
3分题
我挑战
在Rt△ABC中,∠C=90°,若a=3,b=4,
则c=__________;
思考:若本题中,删去∠C=90°这一条件,答案是否发生变化?
在Rt△ABC中,若a=3,b=4, 则c =_______.
5
“分类讨论”
解题策略:
4分题
我突破
如图,是由四个全等的直角三角形适当拼接后形成的图形,这些直角三角形的两直角边分别为a、b,斜边为c,你能用这个图形验证勾股定理吗?
c
b
a
a2 +b2 = c2
这个图案被选为2002年在北京召开的国际数学家大会的会徽。
“赵爽弦图”
c
b
a
用赵爽弦图证明勾股定理
=
b
a
a
我了解
4分题
机会总是留给
有勇气、有准备的人!
直接得1分!!
1分题
我勇敢
4分题
我有感悟,我有收获…
我成功
解法的多元化
“殊途同归”
http://blog..cn/s/blog_a595144c0101f1a1.html
勾股定理的多种证明知识链接:
(a + b)(b + a) =
a2 +
a2 + b2 = c2
b
b
a
a
c
c
∟
∟
∟
c2
+ 2( )
+ ab
+ b2
=
c2
ab
ab
我展示
a2 + b2 = c2
a2
b2
a2
c2
我展示
谢谢指导!
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
