一元二次方程的复习(一)[上学期]
文档属性
| 名称 | 一元二次方程的复习(一)[上学期] |
|
|
| 格式 | rar | ||
| 文件大小 | 411.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-12-27 00:00:00 | ||
图片预览






文档简介
课件17张PPT。一元二次方程复习课
知识回顾返回一、一元二次方程的概念一般形式:ax2+bx+c=0 (a≠0)对应练习1:
1. 将一元二次方程(x-2)(2x+1)=3x2-5化为一般
形式 .其中二次项系数 ,常数项 . 2. 当m 时,方程mx2-3x=2x2-mx+2 是一元二次方程. 当m 时,方程(m2-4)x2-(m+2)x-3=0是一元一次方程.x2+3x-3=01-3≠2=2 3.已知:关于x的方程 (2m-1)x2-(m-1)x=5m
是一元二次方程, 求:m的取值范围.解:∵ 原方程是一元二次方程,
∴ 2m-1≠0,
∴ m≠ . 4.已知 (m-1)x2+mx=x-1 是 (1)一元二次方程时(2)一元二次方程时,求:m的取值范围.知识回顾二、一元二次方程的解法
1. 一元二次方程的解.
满足方程,有根就是两个2.一元二次方程的几种解法
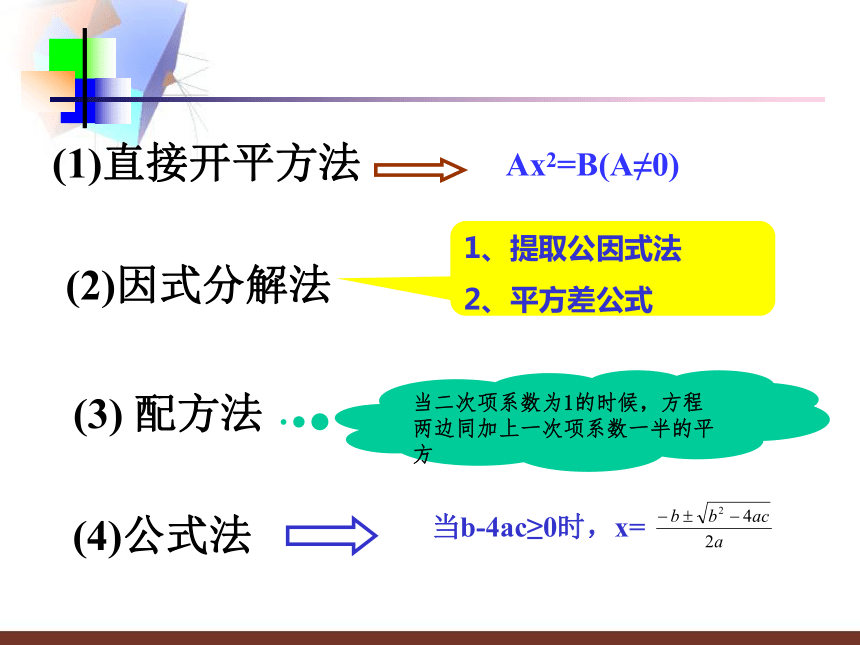
(1)直接开平方法(2)因式分解法
(3) 配方法 (4)公式法(1)直接开平方法Ax2=B(A≠0)(2)因式分解法1、提取公因式法
2、平方差公式(3) 配方法当二次项系数为1的时候,方程两边同加上一次项系数一半的平方(4)公式法当b-4ac≥0时,x=例.选择适当的方法解下列方程: ①
②
③
例. 解方程
① (x+1)(x-1)=2x
② 2(x-2)2+5(x-2)=0
③ (2m+3)2=2(4m+7)总结:方程中有括号时,应先用整体思想考虑有没有简单方法,
若看不出合适的方法时,则把它去括号并整理为一般形式再选
取合理的方法。谁最快选择适当的方法解下列方程:知识回顾对应练习2:
1.一元二次方程3x2=2x的解是 .2.一元二次方程(m-2)x2+3x+m2-4=0有一解为0,则m的值是 .3.已知m是方程x2-x-2=0的一个根,那么代数式m2-m = .x1=0,x2=m=-222知识回顾对应练习3:解下列方程
1.(x+5)(x-5)=7 2.x(x-1)=3-3x3.x2-4x+4=0 4.3x2+x-1=05.x2-x-12=0 6.x2+6x=8
7.m2-10m+24=0返回基础题三、一元二次方程与其他知识结合1.一元二次方程与分式结合知识回顾2.一元二次方程与几何图形结合典型题:若一元二次方程x2-11x+28=0的两根恰好是一等腰三角形的两边,则该三角形的周长是 .知识回顾3.一元二次方程与实际应用结合典型题:
某林场原有森林木材存量为a,木材每年以25%的增长率生长,而每年冬天要砍伐的木材量是x,则经过一年木材存量达到 ,经过两年木材存量达到 .知识回顾返回 某市场销售一批名牌衬衫,平均每天可销售20件,每件赢利40元。为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当降价措施。经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件。 求(1)若商场平均每天要赢利1200元,每件衬衫应降价多少元? (2)要使商场平均每天赢利最多,请你帮助设计方案。X(1)(20+2x)(40-x)=1200Y元(2)y=(20+2x)(40-x)1、若a2+a-1=0,b2+b-1=0,求a/b+b/a的值。拔尖提高2、若 有解,则须满足什么 。3、若关于x的方程(k-1)x2-k2x-1=0的一个根是-1,求 k值,并求其他的根。4、在一次会议上,每两个人相互握一次手,有人统计一共握手66次,问这次会议一共多少人?返回5、如图,AO=BO=50cm,OC是射线,蚂蚁甲以2cm/s的速度从A爬到B,蚂蚁乙以3cm/s的速度从O到C,问:经过几秒两只蚂蚁和O点围成的三角形的面积为450cm2?拔尖提高返回
知识回顾返回一、一元二次方程的概念一般形式:ax2+bx+c=0 (a≠0)对应练习1:
1. 将一元二次方程(x-2)(2x+1)=3x2-5化为一般
形式 .其中二次项系数 ,常数项 . 2. 当m 时,方程mx2-3x=2x2-mx+2 是一元二次方程. 当m 时,方程(m2-4)x2-(m+2)x-3=0是一元一次方程.x2+3x-3=01-3≠2=2 3.已知:关于x的方程 (2m-1)x2-(m-1)x=5m
是一元二次方程, 求:m的取值范围.解:∵ 原方程是一元二次方程,
∴ 2m-1≠0,
∴ m≠ . 4.已知 (m-1)x2+mx=x-1 是 (1)一元二次方程时(2)一元二次方程时,求:m的取值范围.知识回顾二、一元二次方程的解法
1. 一元二次方程的解.
满足方程,有根就是两个2.一元二次方程的几种解法
(1)直接开平方法(2)因式分解法
(3) 配方法 (4)公式法(1)直接开平方法Ax2=B(A≠0)(2)因式分解法1、提取公因式法
2、平方差公式(3) 配方法当二次项系数为1的时候,方程两边同加上一次项系数一半的平方(4)公式法当b-4ac≥0时,x=例.选择适当的方法解下列方程: ①
②
③
例. 解方程
① (x+1)(x-1)=2x
② 2(x-2)2+5(x-2)=0
③ (2m+3)2=2(4m+7)总结:方程中有括号时,应先用整体思想考虑有没有简单方法,
若看不出合适的方法时,则把它去括号并整理为一般形式再选
取合理的方法。谁最快选择适当的方法解下列方程:知识回顾对应练习2:
1.一元二次方程3x2=2x的解是 .2.一元二次方程(m-2)x2+3x+m2-4=0有一解为0,则m的值是 .3.已知m是方程x2-x-2=0的一个根,那么代数式m2-m = .x1=0,x2=m=-222知识回顾对应练习3:解下列方程
1.(x+5)(x-5)=7 2.x(x-1)=3-3x3.x2-4x+4=0 4.3x2+x-1=05.x2-x-12=0 6.x2+6x=8
7.m2-10m+24=0返回基础题三、一元二次方程与其他知识结合1.一元二次方程与分式结合知识回顾2.一元二次方程与几何图形结合典型题:若一元二次方程x2-11x+28=0的两根恰好是一等腰三角形的两边,则该三角形的周长是 .知识回顾3.一元二次方程与实际应用结合典型题:
某林场原有森林木材存量为a,木材每年以25%的增长率生长,而每年冬天要砍伐的木材量是x,则经过一年木材存量达到 ,经过两年木材存量达到 .知识回顾返回 某市场销售一批名牌衬衫,平均每天可销售20件,每件赢利40元。为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当降价措施。经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件。 求(1)若商场平均每天要赢利1200元,每件衬衫应降价多少元? (2)要使商场平均每天赢利最多,请你帮助设计方案。X(1)(20+2x)(40-x)=1200Y元(2)y=(20+2x)(40-x)1、若a2+a-1=0,b2+b-1=0,求a/b+b/a的值。拔尖提高2、若 有解,则须满足什么 。3、若关于x的方程(k-1)x2-k2x-1=0的一个根是-1,求 k值,并求其他的根。4、在一次会议上,每两个人相互握一次手,有人统计一共握手66次,问这次会议一共多少人?返回5、如图,AO=BO=50cm,OC是射线,蚂蚁甲以2cm/s的速度从A爬到B,蚂蚁乙以3cm/s的速度从O到C,问:经过几秒两只蚂蚁和O点围成的三角形的面积为450cm2?拔尖提高返回
同课章节目录
