一元二次方程反思与感悟[上学期]
文档属性
| 名称 | 一元二次方程反思与感悟[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 11.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-09-23 11:37:00 | ||
图片预览








文档简介
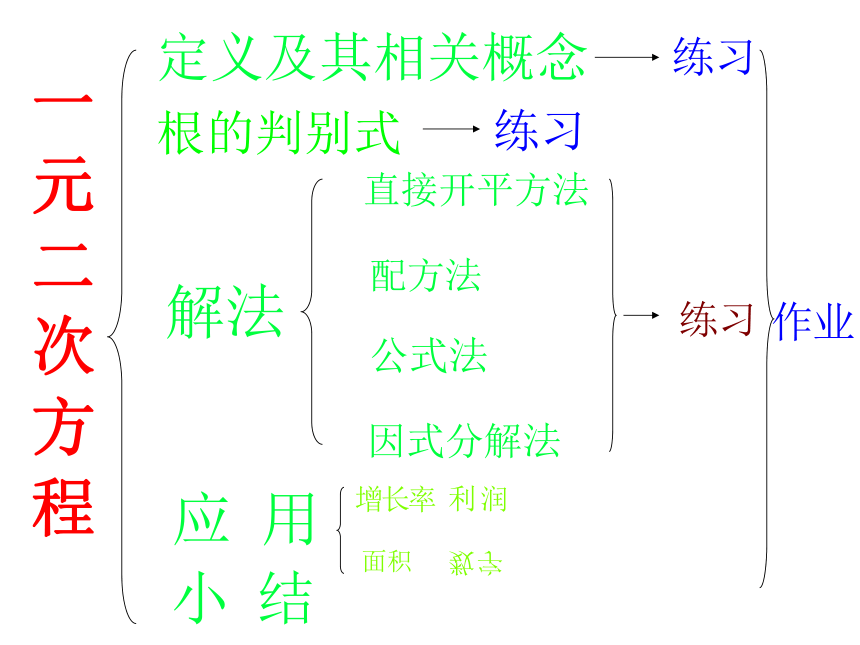
课件25张PPT。教学目标:了解一元二次方程及其相关概念,会用配方法、公式法、分解因式法解简单的一元二次方程(数字系数)
能够利用一元二次方程解决有关的实际问题,并根据具体问题的实际意义检验结果的合理性,进一步培养学生分析问题、解决问题的意识和能力。一 元 二 次 方 程 定义:一元二次方程各项及其系数: 7x2 - 4 =0
4-7x2=0x2 + x –8=0(x+2)(x-1)=63x2 - 5x +1 =0 3x2=5x-1常数项一次项系数二次项系数
一般形式
方程请你完成下列表格配方法配方法解一元二次方程的解题过程1. 把方程化成一元二次方程的一般形式
2. 把二次项系数化为1
3. 把含有未知数的项放在方程的左边,不含未知 数的项放在方程的右边。
4. 方程的两边同加上一次项系数一半的平方
5. 方程的左边化成完全平方的形式,方程的右边化成非负数
6. 利用直接开平方的方法去解公式法公式法解一元二次方程的解题过程
1. 把方程化成一元二次方程的一般形式
写出方程各项的系数
计算出b2-4ac的值,看b2-4ac的值与0的关系,若b2-4ac的值小于0,则此方程没有实数根 。
当b2-4ac的值大于、等于0时, 代入求根公式 计算出方程的值
分解因式法移项,使方程的右边为0。
将方程化为 x(x-a)=0 或x2 –a2 =0 的形式 。
令每个因式分别为零,得到两个一元一次方程。
解这两个一元一次方程,它们的解就是原方程的解。例 1:指出下列方程中,那些是一元二次方程?(1) 5x-6=0(2) (x-2)(x-3)=x2-5 (3) ax2+bx+c=0(4) 3x-2=6x(5)(6)请说出你的判断依据例2.解下列方程
(1) 3x2-48=0???????????????????????????
(2)(x+a)2=225??
? (3) 2x2+7x-4=0????????????????????????????????????
(4) 2x2-x=5??????????????????????????????????????
(5) (3x-1)2=6x-2???????????????????????????
(6) abx2+a2x-b2x-ab=0??同步练习:用恰当的方法解下列方程:
(1) (3x+1)2-2=0
(2) (x+ )2=(1+ )2
(3) 25(x+3)2-16(x+2)2=0
(4) 3x(x+4)=5(x+4)
(5) (2x+1)2+3(2x+1)+2=0
(6) (x+3)(x-1)=5
例4. 某工厂计划在两年内把产量翻一番,如果每年比上年提高的百分数相同,求这个百分数(精确到1%)小结: 本节我们主要学习了一元二次方程的解法和应用,要求大家作到以下几点:
会判断一个方程是不是一元二次方程,能够熟练地将一元二次方程化为一般形式,并准确地写出其各项的系数。
会推导一元二次方程的求根公式,能灵活运用一元二次方程的三种基本解法求方程的解。
能够列出一元二次方程解决面积问题、数字问题、平均增长率(或降低率)问题,特别是平均增长率问题是中考命题的热点。
1.已知关于x的一元二次方程x2-(m+2)x+ m2-2=0 当为何值时,这个方程有两个相等的实数根利润问题某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量减少20千克,现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?解题过程1.当b2-4ac>0时,方程有两个不相 等的实数根;
2.当b2-4ac=0时,方程有两个 相等的实数根;
3.当b2-4ac<0时,方程没有实数根
根的判别式
解:设每千克水果应涨价x元, 依题意得: (500-20x)(10+x)=6000
整理得: x2-15x+50=0
解这个方程得:x1=5 x2=10
要使顾客得到实惠应取x=5
答:每千克水果应涨价 5元.面积有一张长方形的桌子,长6尺,宽3尺,有一块台布的面积是桌面面积的2倍,铺在桌面上时,各边垂下的长度相同,求台布的长和宽各是多少?(精确到0.1尺)数字一个两位数,个位上的数字是十位数字的平方还多1,若把个位上的数字与十位上的数字对调,所得的两位数比原数大27,求原两位数。利润某电视机专卖店出售一种新面市的电视机,平均每天售出50台,每台盈利400元。为了扩 大销售,增加利润,专卖店决定采取适当降价的措施。经调查发现,如果每台电视机每降价 10元,平均每天可多售出5台。专卖店降价第一天,获利30000元。问:每台电视机降价多少 元? ①根据图中所提供的信息回答下列问题:2003年底的绿地面积为 公顷,比2002年底增加了 公顷;在2001年,2002年,2003年这三个中,绿地面积最多的是_______年;
②为满足城市发展的需要,计划到
2005年底使城区绿地面积达到72.6
公顷,试求今明两年绿地面积的
年平均增长率。
?
?
美化城市,改善人们的居住环境已成为城市建设的一项重要内容。我市近几年来,通过拆迁旧房,植草,栽树,修公园等措施,使城区绿地面积不断增加(如图所示)。
相信自己60420031. 审清题意,弄清题中的已知量和未知量找出题中的等量关系。
2. 恰当地设出未知数,用未知数的代数式表示未知量。
3. 根据题中的等量关系列出方程。
4. 解方程得出方程的解。
5. 检验看方程的解是否符合题意。
6. 作答注意单位。列方程解应用题的解题过程。作业:谢谢大家,欢迎批评指正,多提宝贵意见。
能够利用一元二次方程解决有关的实际问题,并根据具体问题的实际意义检验结果的合理性,进一步培养学生分析问题、解决问题的意识和能力。一 元 二 次 方 程 定义:一元二次方程各项及其系数: 7x2 - 4 =0
4-7x2=0x2 + x –8=0(x+2)(x-1)=63x2 - 5x +1 =0 3x2=5x-1常数项一次项系数二次项系数
一般形式
方程请你完成下列表格配方法配方法解一元二次方程的解题过程1. 把方程化成一元二次方程的一般形式
2. 把二次项系数化为1
3. 把含有未知数的项放在方程的左边,不含未知 数的项放在方程的右边。
4. 方程的两边同加上一次项系数一半的平方
5. 方程的左边化成完全平方的形式,方程的右边化成非负数
6. 利用直接开平方的方法去解公式法公式法解一元二次方程的解题过程
1. 把方程化成一元二次方程的一般形式
写出方程各项的系数
计算出b2-4ac的值,看b2-4ac的值与0的关系,若b2-4ac的值小于0,则此方程没有实数根 。
当b2-4ac的值大于、等于0时, 代入求根公式 计算出方程的值
分解因式法移项,使方程的右边为0。
将方程化为 x(x-a)=0 或x2 –a2 =0 的形式 。
令每个因式分别为零,得到两个一元一次方程。
解这两个一元一次方程,它们的解就是原方程的解。例 1:指出下列方程中,那些是一元二次方程?(1) 5x-6=0(2) (x-2)(x-3)=x2-5 (3) ax2+bx+c=0(4) 3x-2=6x(5)(6)请说出你的判断依据例2.解下列方程
(1) 3x2-48=0???????????????????????????
(2)(x+a)2=225??
? (3) 2x2+7x-4=0????????????????????????????????????
(4) 2x2-x=5??????????????????????????????????????
(5) (3x-1)2=6x-2???????????????????????????
(6) abx2+a2x-b2x-ab=0??同步练习:用恰当的方法解下列方程:
(1) (3x+1)2-2=0
(2) (x+ )2=(1+ )2
(3) 25(x+3)2-16(x+2)2=0
(4) 3x(x+4)=5(x+4)
(5) (2x+1)2+3(2x+1)+2=0
(6) (x+3)(x-1)=5
例4. 某工厂计划在两年内把产量翻一番,如果每年比上年提高的百分数相同,求这个百分数(精确到1%)小结: 本节我们主要学习了一元二次方程的解法和应用,要求大家作到以下几点:
会判断一个方程是不是一元二次方程,能够熟练地将一元二次方程化为一般形式,并准确地写出其各项的系数。
会推导一元二次方程的求根公式,能灵活运用一元二次方程的三种基本解法求方程的解。
能够列出一元二次方程解决面积问题、数字问题、平均增长率(或降低率)问题,特别是平均增长率问题是中考命题的热点。
1.已知关于x的一元二次方程x2-(m+2)x+ m2-2=0 当为何值时,这个方程有两个相等的实数根利润问题某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量减少20千克,现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?解题过程1.当b2-4ac>0时,方程有两个不相 等的实数根;
2.当b2-4ac=0时,方程有两个 相等的实数根;
3.当b2-4ac<0时,方程没有实数根
根的判别式
解:设每千克水果应涨价x元, 依题意得: (500-20x)(10+x)=6000
整理得: x2-15x+50=0
解这个方程得:x1=5 x2=10
要使顾客得到实惠应取x=5
答:每千克水果应涨价 5元.面积有一张长方形的桌子,长6尺,宽3尺,有一块台布的面积是桌面面积的2倍,铺在桌面上时,各边垂下的长度相同,求台布的长和宽各是多少?(精确到0.1尺)数字一个两位数,个位上的数字是十位数字的平方还多1,若把个位上的数字与十位上的数字对调,所得的两位数比原数大27,求原两位数。利润某电视机专卖店出售一种新面市的电视机,平均每天售出50台,每台盈利400元。为了扩 大销售,增加利润,专卖店决定采取适当降价的措施。经调查发现,如果每台电视机每降价 10元,平均每天可多售出5台。专卖店降价第一天,获利30000元。问:每台电视机降价多少 元? ①根据图中所提供的信息回答下列问题:2003年底的绿地面积为 公顷,比2002年底增加了 公顷;在2001年,2002年,2003年这三个中,绿地面积最多的是_______年;
②为满足城市发展的需要,计划到
2005年底使城区绿地面积达到72.6
公顷,试求今明两年绿地面积的
年平均增长率。
?
?
美化城市,改善人们的居住环境已成为城市建设的一项重要内容。我市近几年来,通过拆迁旧房,植草,栽树,修公园等措施,使城区绿地面积不断增加(如图所示)。
相信自己60420031. 审清题意,弄清题中的已知量和未知量找出题中的等量关系。
2. 恰当地设出未知数,用未知数的代数式表示未知量。
3. 根据题中的等量关系列出方程。
4. 解方程得出方程的解。
5. 检验看方程的解是否符合题意。
6. 作答注意单位。列方程解应用题的解题过程。作业:谢谢大家,欢迎批评指正,多提宝贵意见。
同课章节目录
