一元二次方程根与系数的关系及其应用(含答案)[上学期]
文档属性
| 名称 | 一元二次方程根与系数的关系及其应用(含答案)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 70.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-02-20 00:00:00 | ||
图片预览


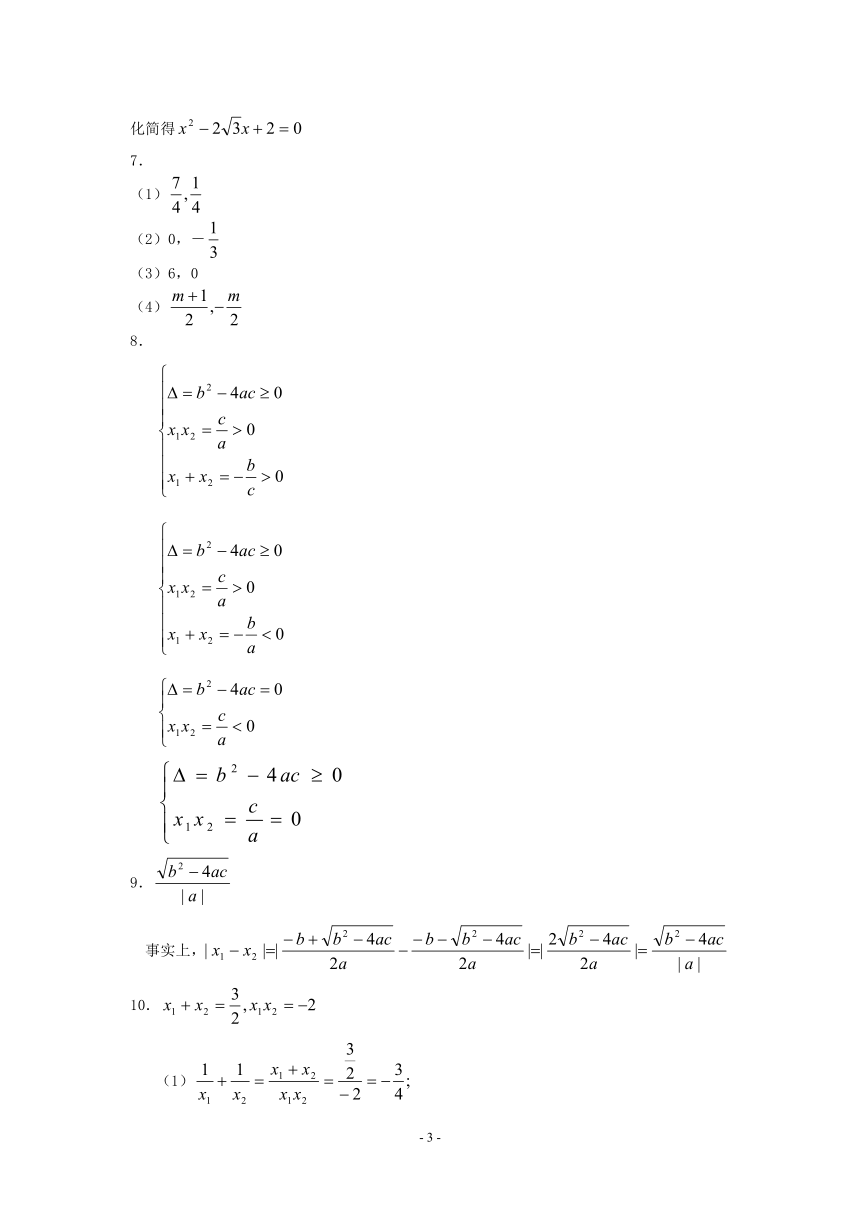
文档简介
一元二次方程根与系数的关系及其应用
A卷
1.如果的两根为,则
2.如果的两根为,那么
3.对于一元二次方程,如果两根互为相反数,那么m = _____________,如果两根互为倒数,那么n = ___________。
4.以两数为根的一元二次方程(二次项系数为1)是______________。
5.若两数和为3,积为-4,则这两个数分别为_____________。
6.的根为方程是______________。
7.不解方程,求下列方程两根之和与两根之积:
(1)
(2)
(3)
(4)
8.设一元二次方程的两根为,若,则___________;若,则______________;若,则___________;若,则___________;
9.设一元二次方程的两根为,则||=_____________。
10.已知方程不解方程求下列各式的值,
(1)=____________;(2)=______________;(3)=____________;
(4)=_________;(5)=__________;(6)=_____;
B卷
1.已知方程的两根的平方和为5,则m=__________。
2.设方程的大根为a,方程的小根为b,则a-b=_____________。
3.设分别是方程的两根,则=_____________。
4.如果方程的根之比等于常数K,则系数a,b,c之间的关系是____________。
5.已知是一元二次方程的两个实数根,且,则m=__________。
6.设的两实数根为,那么为两根的一元二次方程是____________。
7.已知是方程的两实根,是否能适当选取a的值,使得
的值等于________________。
8.关于x的二次方程的两根一个比1大,另一个比1小,则m的取值范围是______________。
9.已知二次方程的两根都是负数,则k的取值范围是____________。
10.方程的两个实根,且这两根的平方和比这两根之积大21,那么m = ______________。
答案
1.
2.-p, q
3.0,1
4.
5.4,-1这两个数是方程的两根
6.
化简得
7.
(1)
(2)0,-
(3)6,0
(4)
8.
9.
事实上,
10.
(1)
(2)
(3)
(4)
(5)
(6)∵
∴
B卷
1. 设 的两根分别为,则
而
即
2.由观察知,1是方程的根,
由韦达定理知,另一根为。
于是a = 1,又从观察知,1也是方程的根,
所以由韦达定理知它的另一根为-1999,
从而 b = - 1999,故a – b = 1 – ( -1999)=2000.
2. 由于分别是方程的根,
故有:
即
从而
而
从而知
4.设方程的两要有为,且由韦达定理知
由此两式消去得即
5.∴方程有两个实数根,由韦达定理知
∵而由知,异号。
故令则得
从上面两式消去k,得
即解之得
6.由韦达定理知
所以
所以,以为两根的一元二次方程为
7.显然a≠0由=得a < 0
由韦达定理知 所以
若有则
∴ a = 9,这与a < 0 矛盾,
故不存在a,使
8.设方程有两个根为,由韦达定理得
又由已知,有
故有
∴
9.高此方程丙实根为,由已知得
∴
即
10.由已知得>0,高两根为,有
由=
∴ m < 0,由,得
即
亦即
∴于是
又∵ m < 0, ∴m = - 1
- 1 -
A卷
1.如果的两根为,则
2.如果的两根为,那么
3.对于一元二次方程,如果两根互为相反数,那么m = _____________,如果两根互为倒数,那么n = ___________。
4.以两数为根的一元二次方程(二次项系数为1)是______________。
5.若两数和为3,积为-4,则这两个数分别为_____________。
6.的根为方程是______________。
7.不解方程,求下列方程两根之和与两根之积:
(1)
(2)
(3)
(4)
8.设一元二次方程的两根为,若,则___________;若,则______________;若,则___________;若,则___________;
9.设一元二次方程的两根为,则||=_____________。
10.已知方程不解方程求下列各式的值,
(1)=____________;(2)=______________;(3)=____________;
(4)=_________;(5)=__________;(6)=_____;
B卷
1.已知方程的两根的平方和为5,则m=__________。
2.设方程的大根为a,方程的小根为b,则a-b=_____________。
3.设分别是方程的两根,则=_____________。
4.如果方程的根之比等于常数K,则系数a,b,c之间的关系是____________。
5.已知是一元二次方程的两个实数根,且,则m=__________。
6.设的两实数根为,那么为两根的一元二次方程是____________。
7.已知是方程的两实根,是否能适当选取a的值,使得
的值等于________________。
8.关于x的二次方程的两根一个比1大,另一个比1小,则m的取值范围是______________。
9.已知二次方程的两根都是负数,则k的取值范围是____________。
10.方程的两个实根,且这两根的平方和比这两根之积大21,那么m = ______________。
答案
1.
2.-p, q
3.0,1
4.
5.4,-1这两个数是方程的两根
6.
化简得
7.
(1)
(2)0,-
(3)6,0
(4)
8.
9.
事实上,
10.
(1)
(2)
(3)
(4)
(5)
(6)∵
∴
B卷
1. 设 的两根分别为,则
而
即
2.由观察知,1是方程的根,
由韦达定理知,另一根为。
于是a = 1,又从观察知,1也是方程的根,
所以由韦达定理知它的另一根为-1999,
从而 b = - 1999,故a – b = 1 – ( -1999)=2000.
2. 由于分别是方程的根,
故有:
即
从而
而
从而知
4.设方程的两要有为,且由韦达定理知
由此两式消去得即
5.∴方程有两个实数根,由韦达定理知
∵而由知,异号。
故令则得
从上面两式消去k,得
即解之得
6.由韦达定理知
所以
所以,以为两根的一元二次方程为
7.显然a≠0由=得a < 0
由韦达定理知 所以
若有则
∴ a = 9,这与a < 0 矛盾,
故不存在a,使
8.设方程有两个根为,由韦达定理得
又由已知,有
故有
∴
9.高此方程丙实根为,由已知得
∴
即
10.由已知得>0,高两根为,有
由=
∴ m < 0,由,得
即
亦即
∴于是
又∵ m < 0, ∴m = - 1
- 1 -
同课章节目录
