苏教版(2019)必修第一册8.1.1函数的零点 课件(共33张PPT)
文档属性
| 名称 | 苏教版(2019)必修第一册8.1.1函数的零点 课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-05 00:00:00 | ||
图片预览










文档简介
(共33张PPT)
第8章
8.1
二分法与求方程近似解
8.1.1 函数的零点
学习目标
1.在二次函数的零点概念基础上,进一步理解一般函数零点的概念.
2. 通过对二次函数的研究,归纳出零点存在定理,并会用零点存在定理分析函数的零点.
核心素养:直观想象、逻辑推理.
新知学习
一、二次函数的零点
一般地,使二次函数y=ax2+bx+c(a,b,c∈R,a≠0)的值为0的实数x称为二次函数y=ax2+bx+c的零点.因此,二次函数y=ax2+bx+c的零点就是关于x的一元二次方程ax2+bx+c=0的实数解,也是二次函数y=ax2+bx+c的图象与x轴交点的横坐标.
二次函数y=ax2+bx+c(a>0)的图象、零点及对应一元二次方程根的关系如下表(a<0,函数图象开口向下,其他同表格).
Δ=b2-4ac ax2+bx+c=0的根 y=ax2+bx+c的图象 图象与x轴交点的横坐标 y=ax2+bx+c的零点
Δ>0 (x1,0), (x2,0) x1,x2
Δ=0
Δ<0 方程无实根 无交点 无零点
二、函数的零点
1.函数的零点
一般地,我们把使函数y=f(x)的值为0的实数x 称为函数y=f(x)的零点.
因此,函数y=f(x)的零点就是方程f(x)=0的实数解.从图象上看,函数y=f(x)的零点,就是它的图象与x轴交点的横坐标.
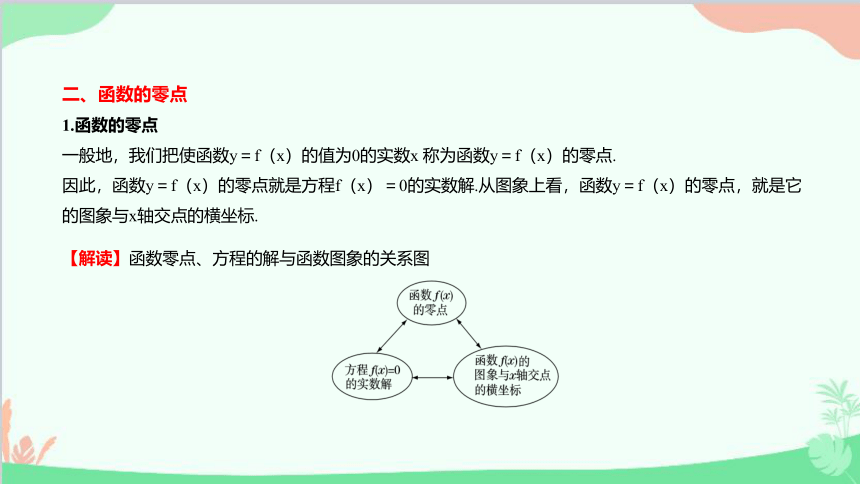
【解读】函数零点、方程的解与函数图象的关系图
2.零点与奇偶性的关系
若定义域包括0的函数y=f (x)具有奇偶性,而且其所有零点组成的集合为A,其中A是一个有限集,则:
(1)若y=f(x)是奇函数,则0∈A,而且A中的元素个数一定是奇数;
(2)若A中的元素个数是偶数,则y=f(x)是偶函数;
(3)若A中的元素个数是奇数且y=f(x)是偶函数,则0∈A;
(4)A中所有元素之和为0.
C
D
【方法技巧】解决函数零点问题的两种方法
(1)代数法:
若方程f(x)=0可解,其实数解就是函数y=f(x)的零点.
(2)几何法:
若方程f(x)=0难以直接求解,将其改写为g(x)- h(x)=0,进一步改写为g(x)=h(x),在同一坐标系中分别作出y=g(x)和y=h(x)的图象,两图象交点的横坐标就是函数y=f(x)的零点,两图象交点的个数就是函数y=f(x)零点的个数.
三、函数零点存在定理
1.函数零点存在定理
若函数y=f(x)在区间[a,b]上的图象是一条不间断的曲线,且f(a)f(b)<0,则函数y=f(x)在区间(a,b)上有零点.
2.函数零点存在定理的几何意义
在闭区间[a,b]上是连续不断的曲线y=f(x),若曲线的起始点(a,f(a))与终点(b,f(b))分别在x轴的两侧,则连续曲线与x轴至少有一个交点.
3.函数零点的性质
对于任意函数y=f(x)的图象是连续不断的一条曲线,则有:
(1)当函数图象通过零点(不是二重零点)且穿过x轴时,函数值变号.
(2)若存在两个或两个以上的零点,那么相邻两个零点之间的所有函数值保持同号.
【概念理解】
(1)函数零点存在定理的两个条件:
①函数f(x)在区间[a,b]上的图象是一条连续不断的曲线;
② f(a)·f(b)<0.这两个条件缺一不可,否则结论不一定成立.
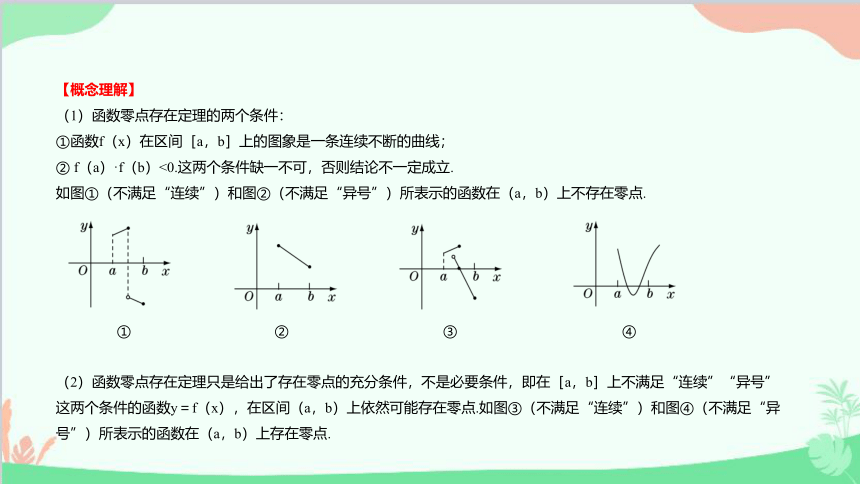
如图①(不满足“连续”)和图②(不满足“异号”)所表示的函数在(a,b)上不存在零点.
① ② ③ ④
(2)函数零点存在定理只是给出了存在零点的充分条件,不是必要条件,即在[a,b]上不满足“连续”“异号”这两个条件的函数y=f(x),在区间(a,b)上依然可能存在零点.如图③(不满足“连续”)和图④(不满足“异号”)所表示的函数在(a,b)上存在零点.
(1,4)
B
2.如果方程f(x)=0有两个相等的实数根x,那么x叫做函数y=f(x)的二重零点.
如,2就是函数f(x)=(x-2)2的二重零点.
【知识拓展】
1.函数零点的分类
(1)变号零点:零点附近两侧的函数值异号,如图①.
(2)不变号零点:零点附近两侧的函数值同号,如图②.
① ②
根的分布 图象 条件
x1k四、一元二次方程根的分布
二次函数零点问题可转化为一元二次方程根的分布问题,可利用二次函数图象与x轴的交点情况来研究.一般从开口方向、对称轴位置、判别式Δ的符号以及端点函数值的符号等方面考虑.
设f(x)=ax2+bx+c(a>0),则f(x)的零点可用一元二次方程ax2+bx+c=0的根来研究.
设x1,x2是方程ax2+bx+c=0(a>0)的两根(不妨设x1根的分布 图象 条件
x1x1,x2∈ (k1,k2)
x1,x2有且 仅有一个在 (k1,k2)内
一元二次方程ax2+bx+c=0(a<0)的根的分布情况可类似得到.
示例 若关于x的方程x2-4x+a=0有两个不相等的正根,则a的取值范围为 .
【方法技巧】解决一元二次方程根的分布问题可以从两个角度思考,一是利用方程本身知识求解,如利用方程的求根公式、根与系数的关系等;二是利用方程对应的函数知识求解,如利用函数的图象、函数的性质等.
(0,4)
典例剖析
0
【方法技巧】求函数零点的方法
(1)可通过解方程,求其实数解;(2)可通过作函数图象,利用数形结合求交点的横坐标;(3)分段函数的零点,需要逐段分别求解.
C
2
(2)当x≤0时,令f(x)=0,即x2+2x-3=0,解得x1=-3,x2=1(舍去).
当x>0时,令f(x)=0,即x-2+ln x=0,∴ ln x=-x+2.
在同一直角坐标系中作出函数y=ln x与y=-x+2(x>0)的图象,如图,
由图可知两图象只有一个交点.
综上可知,函数f(x)的零点个数为2.
(1)C (2)2
【方法总结】求函数零点个数的四种方法
1.方程法:求方程f(x)=0的实数根.
2.图象法:将方程f(x)=0与对应函数的图象联系起来找出零点,对于不易画出f(x)=g(x)-h(x)图象的函数分别画出g(x)和h(x)的图象,看两个图象有几个交点.
3.结合函数的奇偶性判断
存在奇偶性的函数的零点(零除外)是成对出现的.因此,研究奇函数或偶函数在区间[-a,a]上的零点时,可以先研究其在区间(0,a]上的零点情况.
4.应用函数零点存在定理结合单调性判断
判断函数y=f(x)在每个单调区间上是否有零点即可确定函数零点的个数.
三、判断零点所在区间
例 3 方程6-2x=ln x必有一根的区间是( )
A.(2,3) B.(3,4) C.(0,1) D.(4,5)
A
【方法技巧】判断函数零点所在区间的方法和步骤
(1)方法:定理法,即利用函数零点存在定理判断.
(2)步骤:①代入,将区间端点代入函数解析式求出函数值.②判断,把所得函数值相乘,并进行符号判断.
③总结,若符号为正且函数在该区间内是单调函数,则函数在该区间内无零点;若符号为负且函数图象连续,则函数在该区间内至少有一个零点.
【分析】构造函数f (x)=2x+ln x-6,然后利用零点存在定理可判断出方程6-2x= ln x的根所在的区间.
【解析】由6-2x=ln x,得2x+ln x-6=0,构造函数f(x)=2x+ln x-6.
∵ f(2)=ln 2-2<0,f(3)=ln 3>0,∴ f(2)f(3)<0,
∴ 由零点存在定理可知,函数f(x)在区间(2,3)上至少有一个零点.
又∵ 函数f(x)在(0,+∞)上单调递增,∴ f(x)在区间(2,3)上至多有一个零点,
∴ 函数f(x)在区间(2,3)上有唯一零点.即方程6-2x=ln x必有一根的区间是(2,3).
四、与零点相关的参数问题
1.根据零点所在区间求参数范围
例 4 若函数f(x)=x+ax(a∈R)在区间(1,2)上有零点,则a的值可能是( )
A.-2 B. 0 C. 1 D. 3
A
【解析】(方法1:验证法)函数f(x)=x+ax(a∈R)的图象在(1,2)上是连续不断的,逐个选项代入验证,当a=-2时,f(1)=1-2<0,f(2)=2-1=1>0,故f(x)在区间(1,2)上有零点,同理,其他选项不符合,故选A.
(方法2:直接法)令x+ax=0,得x2=-a.
又∵ f(x)在区间(1,2)上有零点,∴ a<0且x=-a∈(1,2),∴ -4(方法3:图象法)令x+ax=0,∴ x2=-a.
又∵ f(x)在区间(1,2)上有零点,∴ 函数y=x2的图象与直线y=-a在区间(1,2)上有交点,
如图所示,∴ 1<-a<4,∴ -4【解题通法】根据函数零点个数或零点所在区间求参数的方法
(1)直接法:直接根据题设条件构建关于参数的不等式(组),通过解不等式(组)确定参数的取值范围.
(2)分离参数法:先将参数分离,然后将原问题转化为求函数值域的问题加以解决.
(3)数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后利用数形结合思想求解.
(0,1)
五、关于一元二次方程根的分布问题
例 6 已知关于x的一元二次方程x2+2mx+2m+1=0.
(1)若方程有两个实数根,其中一个根在区间(-1,0)内,另一个根在区间(1,2)内,求m的取值范围.
(2)若方程有两个不相等的实数根,且均在区间(0,1)内,求m的取值范围.
【方法总结】解一元二次方程根的分布问题的四个方向
(1)抛物线开口方向;
(2)一元二次方程根的判别式;
(3)对应区间端点函数值的符号;
(4)抛物线的对称轴与区间端点的位置关系.
随堂小测
C
C
A
AD
BCD
B
[-1,+∞)
2
解: (1)若λ=2,当x≥2时,令x-4<0,得2≤x<4;当x<2时,令x2-4x+3<0,解得1综上可知,1(2)令f(x)=0,当x≥λ时,x=4,
当x<λ时,x2-4x+3=0,解得x=1或x=3.
因为函数f(x)恰有2个零点,结合如图所示的函数图象知,1<λ≤3或λ>4,
故λ的取值范围为(1,3]∪(4,+∞).
谢 谢!
第8章
8.1
二分法与求方程近似解
8.1.1 函数的零点
学习目标
1.在二次函数的零点概念基础上,进一步理解一般函数零点的概念.
2. 通过对二次函数的研究,归纳出零点存在定理,并会用零点存在定理分析函数的零点.
核心素养:直观想象、逻辑推理.
新知学习
一、二次函数的零点
一般地,使二次函数y=ax2+bx+c(a,b,c∈R,a≠0)的值为0的实数x称为二次函数y=ax2+bx+c的零点.因此,二次函数y=ax2+bx+c的零点就是关于x的一元二次方程ax2+bx+c=0的实数解,也是二次函数y=ax2+bx+c的图象与x轴交点的横坐标.
二次函数y=ax2+bx+c(a>0)的图象、零点及对应一元二次方程根的关系如下表(a<0,函数图象开口向下,其他同表格).
Δ=b2-4ac ax2+bx+c=0的根 y=ax2+bx+c的图象 图象与x轴交点的横坐标 y=ax2+bx+c的零点
Δ>0 (x1,0), (x2,0) x1,x2
Δ=0
Δ<0 方程无实根 无交点 无零点
二、函数的零点
1.函数的零点
一般地,我们把使函数y=f(x)的值为0的实数x 称为函数y=f(x)的零点.
因此,函数y=f(x)的零点就是方程f(x)=0的实数解.从图象上看,函数y=f(x)的零点,就是它的图象与x轴交点的横坐标.
【解读】函数零点、方程的解与函数图象的关系图
2.零点与奇偶性的关系
若定义域包括0的函数y=f (x)具有奇偶性,而且其所有零点组成的集合为A,其中A是一个有限集,则:
(1)若y=f(x)是奇函数,则0∈A,而且A中的元素个数一定是奇数;
(2)若A中的元素个数是偶数,则y=f(x)是偶函数;
(3)若A中的元素个数是奇数且y=f(x)是偶函数,则0∈A;
(4)A中所有元素之和为0.
C
D
【方法技巧】解决函数零点问题的两种方法
(1)代数法:
若方程f(x)=0可解,其实数解就是函数y=f(x)的零点.
(2)几何法:
若方程f(x)=0难以直接求解,将其改写为g(x)- h(x)=0,进一步改写为g(x)=h(x),在同一坐标系中分别作出y=g(x)和y=h(x)的图象,两图象交点的横坐标就是函数y=f(x)的零点,两图象交点的个数就是函数y=f(x)零点的个数.
三、函数零点存在定理
1.函数零点存在定理
若函数y=f(x)在区间[a,b]上的图象是一条不间断的曲线,且f(a)f(b)<0,则函数y=f(x)在区间(a,b)上有零点.
2.函数零点存在定理的几何意义
在闭区间[a,b]上是连续不断的曲线y=f(x),若曲线的起始点(a,f(a))与终点(b,f(b))分别在x轴的两侧,则连续曲线与x轴至少有一个交点.
3.函数零点的性质
对于任意函数y=f(x)的图象是连续不断的一条曲线,则有:
(1)当函数图象通过零点(不是二重零点)且穿过x轴时,函数值变号.
(2)若存在两个或两个以上的零点,那么相邻两个零点之间的所有函数值保持同号.
【概念理解】
(1)函数零点存在定理的两个条件:
①函数f(x)在区间[a,b]上的图象是一条连续不断的曲线;
② f(a)·f(b)<0.这两个条件缺一不可,否则结论不一定成立.
如图①(不满足“连续”)和图②(不满足“异号”)所表示的函数在(a,b)上不存在零点.
① ② ③ ④
(2)函数零点存在定理只是给出了存在零点的充分条件,不是必要条件,即在[a,b]上不满足“连续”“异号”这两个条件的函数y=f(x),在区间(a,b)上依然可能存在零点.如图③(不满足“连续”)和图④(不满足“异号”)所表示的函数在(a,b)上存在零点.
(1,4)
B
2.如果方程f(x)=0有两个相等的实数根x,那么x叫做函数y=f(x)的二重零点.
如,2就是函数f(x)=(x-2)2的二重零点.
【知识拓展】
1.函数零点的分类
(1)变号零点:零点附近两侧的函数值异号,如图①.
(2)不变号零点:零点附近两侧的函数值同号,如图②.
① ②
根的分布 图象 条件
x1
二次函数零点问题可转化为一元二次方程根的分布问题,可利用二次函数图象与x轴的交点情况来研究.一般从开口方向、对称轴位置、判别式Δ的符号以及端点函数值的符号等方面考虑.
设f(x)=ax2+bx+c(a>0),则f(x)的零点可用一元二次方程ax2+bx+c=0的根来研究.
设x1,x2是方程ax2+bx+c=0(a>0)的两根(不妨设x1
x1
x1,x2有且 仅有一个在 (k1,k2)内
一元二次方程ax2+bx+c=0(a<0)的根的分布情况可类似得到.
示例 若关于x的方程x2-4x+a=0有两个不相等的正根,则a的取值范围为 .
【方法技巧】解决一元二次方程根的分布问题可以从两个角度思考,一是利用方程本身知识求解,如利用方程的求根公式、根与系数的关系等;二是利用方程对应的函数知识求解,如利用函数的图象、函数的性质等.
(0,4)
典例剖析
0
【方法技巧】求函数零点的方法
(1)可通过解方程,求其实数解;(2)可通过作函数图象,利用数形结合求交点的横坐标;(3)分段函数的零点,需要逐段分别求解.
C
2
(2)当x≤0时,令f(x)=0,即x2+2x-3=0,解得x1=-3,x2=1(舍去).
当x>0时,令f(x)=0,即x-2+ln x=0,∴ ln x=-x+2.
在同一直角坐标系中作出函数y=ln x与y=-x+2(x>0)的图象,如图,
由图可知两图象只有一个交点.
综上可知,函数f(x)的零点个数为2.
(1)C (2)2
【方法总结】求函数零点个数的四种方法
1.方程法:求方程f(x)=0的实数根.
2.图象法:将方程f(x)=0与对应函数的图象联系起来找出零点,对于不易画出f(x)=g(x)-h(x)图象的函数分别画出g(x)和h(x)的图象,看两个图象有几个交点.
3.结合函数的奇偶性判断
存在奇偶性的函数的零点(零除外)是成对出现的.因此,研究奇函数或偶函数在区间[-a,a]上的零点时,可以先研究其在区间(0,a]上的零点情况.
4.应用函数零点存在定理结合单调性判断
判断函数y=f(x)在每个单调区间上是否有零点即可确定函数零点的个数.
三、判断零点所在区间
例 3 方程6-2x=ln x必有一根的区间是( )
A.(2,3) B.(3,4) C.(0,1) D.(4,5)
A
【方法技巧】判断函数零点所在区间的方法和步骤
(1)方法:定理法,即利用函数零点存在定理判断.
(2)步骤:①代入,将区间端点代入函数解析式求出函数值.②判断,把所得函数值相乘,并进行符号判断.
③总结,若符号为正且函数在该区间内是单调函数,则函数在该区间内无零点;若符号为负且函数图象连续,则函数在该区间内至少有一个零点.
【分析】构造函数f (x)=2x+ln x-6,然后利用零点存在定理可判断出方程6-2x= ln x的根所在的区间.
【解析】由6-2x=ln x,得2x+ln x-6=0,构造函数f(x)=2x+ln x-6.
∵ f(2)=ln 2-2<0,f(3)=ln 3>0,∴ f(2)f(3)<0,
∴ 由零点存在定理可知,函数f(x)在区间(2,3)上至少有一个零点.
又∵ 函数f(x)在(0,+∞)上单调递增,∴ f(x)在区间(2,3)上至多有一个零点,
∴ 函数f(x)在区间(2,3)上有唯一零点.即方程6-2x=ln x必有一根的区间是(2,3).
四、与零点相关的参数问题
1.根据零点所在区间求参数范围
例 4 若函数f(x)=x+ax(a∈R)在区间(1,2)上有零点,则a的值可能是( )
A.-2 B. 0 C. 1 D. 3
A
【解析】(方法1:验证法)函数f(x)=x+ax(a∈R)的图象在(1,2)上是连续不断的,逐个选项代入验证,当a=-2时,f(1)=1-2<0,f(2)=2-1=1>0,故f(x)在区间(1,2)上有零点,同理,其他选项不符合,故选A.
(方法2:直接法)令x+ax=0,得x2=-a.
又∵ f(x)在区间(1,2)上有零点,∴ a<0且x=-a∈(1,2),∴ -4
又∵ f(x)在区间(1,2)上有零点,∴ 函数y=x2的图象与直线y=-a在区间(1,2)上有交点,
如图所示,∴ 1<-a<4,∴ -4
(1)直接法:直接根据题设条件构建关于参数的不等式(组),通过解不等式(组)确定参数的取值范围.
(2)分离参数法:先将参数分离,然后将原问题转化为求函数值域的问题加以解决.
(3)数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后利用数形结合思想求解.
(0,1)
五、关于一元二次方程根的分布问题
例 6 已知关于x的一元二次方程x2+2mx+2m+1=0.
(1)若方程有两个实数根,其中一个根在区间(-1,0)内,另一个根在区间(1,2)内,求m的取值范围.
(2)若方程有两个不相等的实数根,且均在区间(0,1)内,求m的取值范围.
【方法总结】解一元二次方程根的分布问题的四个方向
(1)抛物线开口方向;
(2)一元二次方程根的判别式;
(3)对应区间端点函数值的符号;
(4)抛物线的对称轴与区间端点的位置关系.
随堂小测
C
C
A
AD
BCD
B
[-1,+∞)
2
解: (1)若λ=2,当x≥2时,令x-4<0,得2≤x<4;当x<2时,令x2-4x+3<0,解得1
当x<λ时,x2-4x+3=0,解得x=1或x=3.
因为函数f(x)恰有2个零点,结合如图所示的函数图象知,1<λ≤3或λ>4,
故λ的取值范围为(1,3]∪(4,+∞).
谢 谢!
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
