高一数学人教版A(2019)必修第二册:9.2.1总体取值规律的统计(含答案)
文档属性
| 名称 | 高一数学人教版A(2019)必修第二册:9.2.1总体取值规律的统计(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 402.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-05 17:32:01 | ||
图片预览



文档简介
9.2.1 总体取值规律的估计
学习目标
了解分布的意义和作用。
会列频率分布表,会画频率分布直方图,理解它们的特点。
会画条形图,扇形图,折线图等统计图,理解它们的特点。
会用样本的频率分布估计总体分布。
会用随机抽样的基本方法和用样本估计总体的思想解绝一些简单的实际问题。
基础梳理
频率分布直方图的画法:
1.求极差.极差为一组数据中最大值与最小值的差。
2.决定组距与组数.
3.将数据分组.
4.列频率分布表..
5.画频率分布直方图.
随堂训练
1、从某小学随机抽取100名学生,将他们的身高数据(单位:厘米)按分组,绘制成频率分布直方图(如图).从身高在三组内的学生中,用分层抽样的方法抽取18人参加一项活动,则从身高在内的学生中选取的人数应为( )
A.3 B.4 C.5 D.6
2、要从已编号(1~60)的60枚最新研制的某型导弹中随机抽取6枚来进行发射试验,用每部分选取的号码间隔一样的系统抽样方法确定所选取的6枚导弹的编号可能是( )
A.5,10,15,20,25,30
B.3,13,23,33,43,53
C.1,2,3,4,5,6
D.2,4,8,16,32,48
3、将参加夏令营的600名学生编号为:001,002,…,600.采用系统抽样方法抽取一个容量为50的样本,且随机抽得的号码为003.这600名学生分住在三个营区,从001到300在第Ⅰ营区,从301到495在第Ⅱ营区,从496到600在第Ⅲ营区,三个营区被抽中的人数依次为( )
A.26,16,8 B.25,17,8 C.25,16,9 D.24,17,9
4、某学校为了解1000名新生的近视情况,将这些学生编号为000,001,002,…,999,从这些新生中用系统抽样的方法抽取100名学生进行检查,若036号学生被抽到,则下面4名学生中被抽到的是( )
A. 008号学生 B. 200号学生 C. 616号学生 D. 815号学生
5、2019年4月份居民消费的各类商品及服务价格环比(与 3月份相比)变动情况如下图:
则下列叙述不正确的是( )
A.八大类消费价格环比呈现四涨四平
B.其他用品和服务价格环比涨幅最大
C.生活用品及服务和医疗保健价格环比涨幅相同
D.4月份居民消费平均价格环比持平
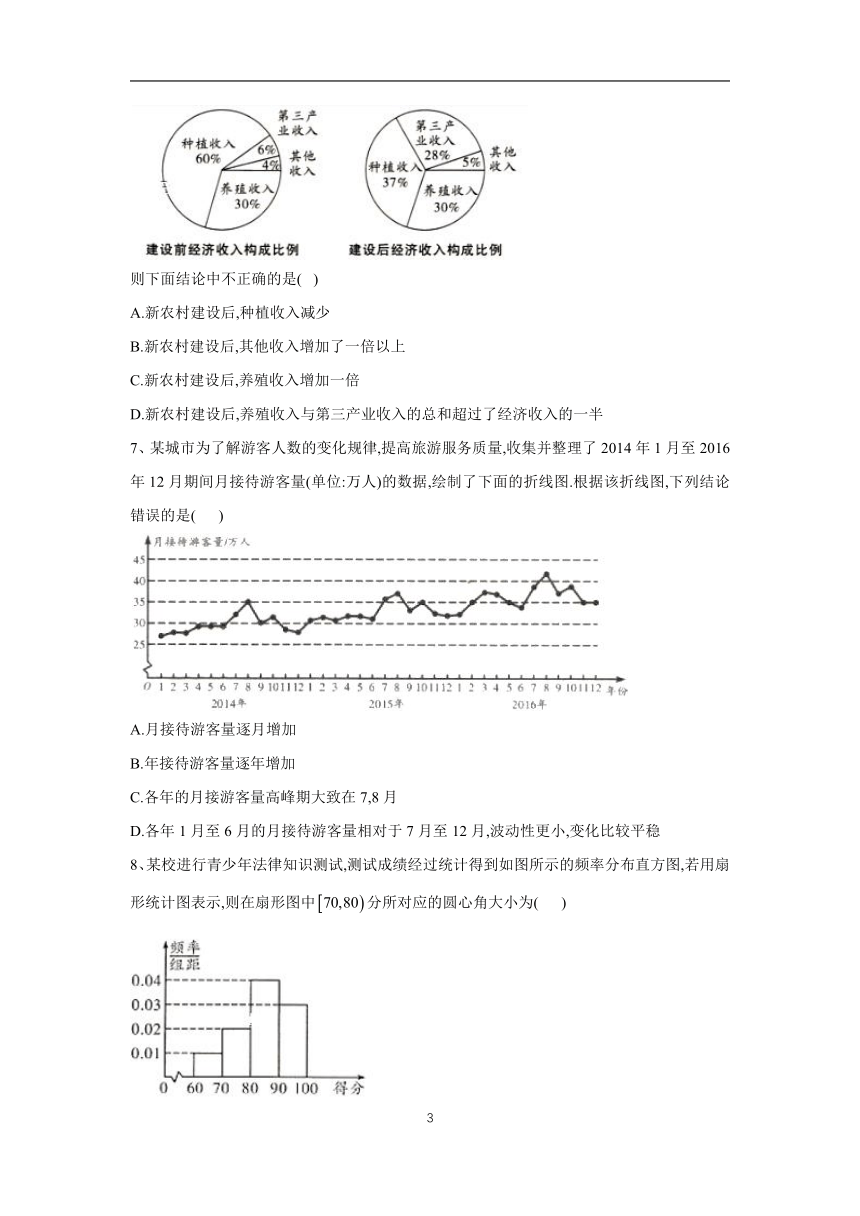
6、某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番。为更好地了解该地区农村的经济收入变化情况,统计了该地区系农村建设前后农村的经济收入构成比例。得到如下饼图:
则下面结论中不正确的是( )
A.新农村建设后,种植收入减少
B.新农村建设后,其他收入增加了一倍以上
C.新农村建设后,养殖收入增加一倍
D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
7、某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是( )
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
8、某校进行青少年法律知识测试,测试成绩经过统计得到如图所示的频率分布直方图,若用扇形统计图表示,则在扇形图中分所对应的圆心角大小为( )
A. B. C. D.
9、学校消防、卫生知识竞赛,将所得成绩制成如图的频率分布直方图(假定每个分数段内的成绩均匀分布),则( )
A.0.200 B.0.020 C.0.150 D.0.015
10、某学校为了解1000名新生的身体素质,将这些学生编号为1,2,…,1000,从这些新生中用系统抽样方法等距抽取100名学生进行体质测验.若46号学生被抽到,则下面4名学生中被抽到的是( )
A.8号学生 B.200号学生 C.616号学生 D.815号学生
11、某单位200名职工的年龄分布情况如图所示.现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1-200编号,并按编号顺序平均分为40组(1-5号,6-10号…,196-200号);若第5组抽出的号码为22,则第8组抽出的号码应是___________.若用分层抽样方法,则40岁以下年龄段应抽取_________人.
12、高三(1)班共有56人,学号依次为1,2,3,…,56,现用系统抽样的方法抽取一个容量为4的样本,已知学号为6,34,48的同学在样本中,那么还有一个同学的学号应为________.
13、某药厂选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:)的分组区间为,将其按从左到右的顺序分别编号为第一组,第二组,…,第五组.如图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,则第三组的人数为__________.
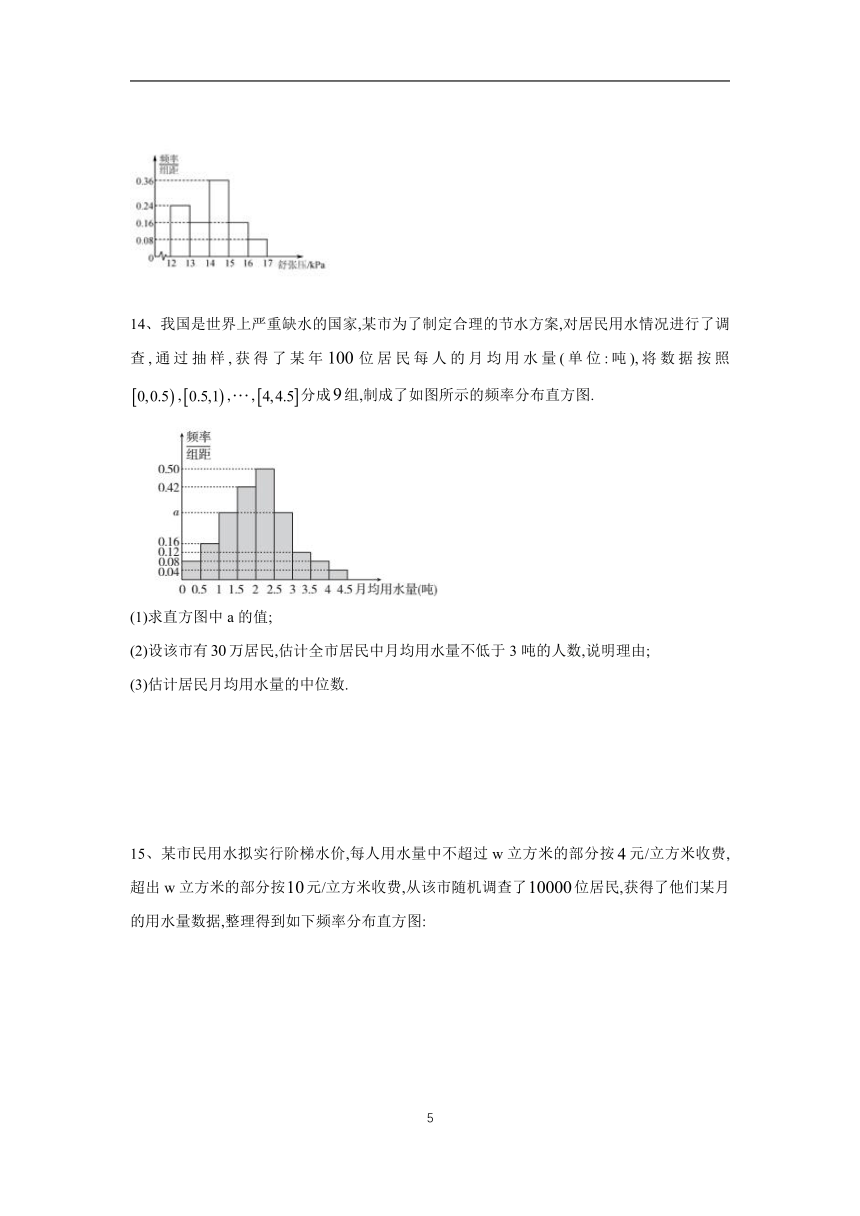
14、我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年位居民每人的月均用水量(单位:吨),将数据按照,,,分成组,制成了如图所示的频率分布直方图.
(1)求直方图中a的值;
(2)设该市有万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由;
(3)估计居民月均用水量的中位数.
15、某市民用水拟实行阶梯水价,每人用水量中不超过w立方米的部分按元/立方米收费,超出w立方米的部分按元/立方米收费,从该市随机调查了位居民,获得了他们某月的用水量数据,整理得到如下频率分布直方图:
(1)如果w为整数,那么根据此次调查,为使以上居民在该月的用水价格为元/立方米,w至少定为多少
(2)假设同组中的每个数据用该组区间的右端点值代替,当时,估计该市居民该月的人均水费.
答案
随堂训练
1答案及解析:
答案:A
解析:各组频率等于各组矩形的面积,所以,
身高在的频率分别为,
身高在的频数分别为,
分层抽样的比例为 .
所以,身高在内的学生中选取的人数为.
故选A.
2答案及解析:
答案:B
解析:采用系统抽样法从枚某型导弹中随机抽取枚抽样间隔应为,只有B选项中导弹的编号间隔为故选B.
3答案及解析:
答案:B
解析:
本题主要考查系统抽样的意义.依题意及系统抽样的意义可知,将这名学生按编号依次分成50组,每一组各有12名学生,第组抽中的号码是.令得,因此第Ⅰ营区被抽中的人数是25;令得,因此第Ⅱ营区被抽中的人数是.结合各选项知,选B.
4答案及解析:
答案:C
解析:由题意得抽样间隔为,因为036号学生被抽到,所以被抽中的初始编号为006号,之后被抽到的编号均是10的整数倍与6的和,
故选:C.
5答案及解析:
答案:D
解析:在八大类消费中,食品烟酒、衣着、居住、交通和通信价格环比持平,另外四类价格环比均上涨,其中其他用品和服务价格环比涨幅最大,为0.4% ,生活用品及服务和医疗保健价格环比涨幅均为0. 1 % . 4月份居民消费平均价格环比涨幅为.故选 D.
6答案及解析:
答案:A
解析:设建设前总经济收入为100则建设后总经济收入为200
对于A,建设前种植收入为,建设后种植收入为故A借误:
对于B,建设前其他收入为,建设后其他收入为,故B正确
对于C,建设前养殖收入为,建设后养殖收入为,故C正确:
对于D,建设后,养殖收入占,第三产业收入占故D正确:
7答案及解析:
答案:A
解析:A项,由折线图可看出2014年9月接待的游客量小于8月接待的游客量,因此月接待游客量并不是逐月增加的,故A项结论错误符合题意.
B项,由折线图可看出2014年每个月接待的游客量小于2015年对应月份接待的游客量,2015年每个月接待的游客量小于2016年对应月份接待的游客量,所以年接待游客量逐年增加,故B项不符合题意.
C项,由折线图可看出每一年的7,8月接待的游客量远高于当年其他月份,因此各年的月接待游客量高峰期大致在7,8月,故C项不符合题意.
D项,由折线图可看出各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳,故D项不符合题意.
故本题正确答案为A.
8答案及解析:
答案:B
解析:由图可得的频率.所以圆心角.
9答案及解析:
答案:B
解析:由已知得,解得,故选B.
10答案及解析:
答案:C
解析:由已知将1000名学生分成100个组,每组10名学生,用系统抽样,46号学生被抽到,
所以第一组抽到6号,且每组抽到的学生号构成等差数列,公差,
所以,
若,则,不合题意;若,则,不合题意;
若,则,符合题意;若,则,不合题意.故选C.
11答案及解析:
答案:37; 20
解析:由分组可知,抽号的间隔为5,又因为第5组抽出的号码为22,所以第6组抽出的号码为27,第7组抽出的号码为32,第8组抽出的号码为37.
40岁以下年龄段的职工数为,则应抽取的人数为(人).
12答案及解析:
答案:20
解析:从56个学生中用系统抽样的方法抽取一个容量为4的样本,则分组时要分成4个小组,每一个小组有14人.∵学号为6,34,48的同学在样本中,即第一个学号是6,∴第二个抽取的学号是.
13答案及解析:
答案:18
解析:由频率= 以及直方图可得出分布在区间第一组与第二组共有20人,分布在区间第一组与第二组的频率分别为0.24,0.16,设总的人数为n,则,∴,所以第三小组人数为(人).
14答案及解析:
答案:(1)由频率分布直方图可知,月均用水量在的频率为.
同理,在
等组的频率分别为.
由,
解得.
(2).由(1)知, 位居民月均用水量不低于吨的频率为
.
由以上样本的频率分布,
可以估计万居民中月均用水量不低于吨的人数为
.
(3)设中位数为吨.
因为前组的频率之和为
,
而前组的频率之和为,
所以.
由,解得.
故可估计居民月均用水量的中位数为吨.
15答案及解析:
答案:(1)3(2)10.5元
解析: (1)由用水量的频率分布直方图知,该市居民该月用水量在区间,,,,内的频率依次为,所以该月用水量不超过立方米的居民占,用数量不超过立方米的居民占,依题意, 至少定为.
(2)由用水量的频率分布直方图及题意,得居民该月用水费用的数据分组与频率分布表:
组号 1 2 3 4 5 6 7 8
分组
频率 0.1 0.15 0.2 0.25 0.15 0.05 0.05 0.05
根据题意,该市居民该月的人均水费估计为: (元)
2
学习目标
了解分布的意义和作用。
会列频率分布表,会画频率分布直方图,理解它们的特点。
会画条形图,扇形图,折线图等统计图,理解它们的特点。
会用样本的频率分布估计总体分布。
会用随机抽样的基本方法和用样本估计总体的思想解绝一些简单的实际问题。
基础梳理
频率分布直方图的画法:
1.求极差.极差为一组数据中最大值与最小值的差。
2.决定组距与组数.
3.将数据分组.
4.列频率分布表..
5.画频率分布直方图.
随堂训练
1、从某小学随机抽取100名学生,将他们的身高数据(单位:厘米)按分组,绘制成频率分布直方图(如图).从身高在三组内的学生中,用分层抽样的方法抽取18人参加一项活动,则从身高在内的学生中选取的人数应为( )
A.3 B.4 C.5 D.6
2、要从已编号(1~60)的60枚最新研制的某型导弹中随机抽取6枚来进行发射试验,用每部分选取的号码间隔一样的系统抽样方法确定所选取的6枚导弹的编号可能是( )
A.5,10,15,20,25,30
B.3,13,23,33,43,53
C.1,2,3,4,5,6
D.2,4,8,16,32,48
3、将参加夏令营的600名学生编号为:001,002,…,600.采用系统抽样方法抽取一个容量为50的样本,且随机抽得的号码为003.这600名学生分住在三个营区,从001到300在第Ⅰ营区,从301到495在第Ⅱ营区,从496到600在第Ⅲ营区,三个营区被抽中的人数依次为( )
A.26,16,8 B.25,17,8 C.25,16,9 D.24,17,9
4、某学校为了解1000名新生的近视情况,将这些学生编号为000,001,002,…,999,从这些新生中用系统抽样的方法抽取100名学生进行检查,若036号学生被抽到,则下面4名学生中被抽到的是( )
A. 008号学生 B. 200号学生 C. 616号学生 D. 815号学生
5、2019年4月份居民消费的各类商品及服务价格环比(与 3月份相比)变动情况如下图:
则下列叙述不正确的是( )
A.八大类消费价格环比呈现四涨四平
B.其他用品和服务价格环比涨幅最大
C.生活用品及服务和医疗保健价格环比涨幅相同
D.4月份居民消费平均价格环比持平
6、某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番。为更好地了解该地区农村的经济收入变化情况,统计了该地区系农村建设前后农村的经济收入构成比例。得到如下饼图:
则下面结论中不正确的是( )
A.新农村建设后,种植收入减少
B.新农村建设后,其他收入增加了一倍以上
C.新农村建设后,养殖收入增加一倍
D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
7、某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是( )
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
8、某校进行青少年法律知识测试,测试成绩经过统计得到如图所示的频率分布直方图,若用扇形统计图表示,则在扇形图中分所对应的圆心角大小为( )
A. B. C. D.
9、学校消防、卫生知识竞赛,将所得成绩制成如图的频率分布直方图(假定每个分数段内的成绩均匀分布),则( )
A.0.200 B.0.020 C.0.150 D.0.015
10、某学校为了解1000名新生的身体素质,将这些学生编号为1,2,…,1000,从这些新生中用系统抽样方法等距抽取100名学生进行体质测验.若46号学生被抽到,则下面4名学生中被抽到的是( )
A.8号学生 B.200号学生 C.616号学生 D.815号学生
11、某单位200名职工的年龄分布情况如图所示.现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1-200编号,并按编号顺序平均分为40组(1-5号,6-10号…,196-200号);若第5组抽出的号码为22,则第8组抽出的号码应是___________.若用分层抽样方法,则40岁以下年龄段应抽取_________人.
12、高三(1)班共有56人,学号依次为1,2,3,…,56,现用系统抽样的方法抽取一个容量为4的样本,已知学号为6,34,48的同学在样本中,那么还有一个同学的学号应为________.
13、某药厂选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:)的分组区间为,将其按从左到右的顺序分别编号为第一组,第二组,…,第五组.如图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,则第三组的人数为__________.
14、我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年位居民每人的月均用水量(单位:吨),将数据按照,,,分成组,制成了如图所示的频率分布直方图.
(1)求直方图中a的值;
(2)设该市有万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由;
(3)估计居民月均用水量的中位数.
15、某市民用水拟实行阶梯水价,每人用水量中不超过w立方米的部分按元/立方米收费,超出w立方米的部分按元/立方米收费,从该市随机调查了位居民,获得了他们某月的用水量数据,整理得到如下频率分布直方图:
(1)如果w为整数,那么根据此次调查,为使以上居民在该月的用水价格为元/立方米,w至少定为多少
(2)假设同组中的每个数据用该组区间的右端点值代替,当时,估计该市居民该月的人均水费.
答案
随堂训练
1答案及解析:
答案:A
解析:各组频率等于各组矩形的面积,所以,
身高在的频率分别为,
身高在的频数分别为,
分层抽样的比例为 .
所以,身高在内的学生中选取的人数为.
故选A.
2答案及解析:
答案:B
解析:采用系统抽样法从枚某型导弹中随机抽取枚抽样间隔应为,只有B选项中导弹的编号间隔为故选B.
3答案及解析:
答案:B
解析:
本题主要考查系统抽样的意义.依题意及系统抽样的意义可知,将这名学生按编号依次分成50组,每一组各有12名学生,第组抽中的号码是.令得,因此第Ⅰ营区被抽中的人数是25;令得,因此第Ⅱ营区被抽中的人数是.结合各选项知,选B.
4答案及解析:
答案:C
解析:由题意得抽样间隔为,因为036号学生被抽到,所以被抽中的初始编号为006号,之后被抽到的编号均是10的整数倍与6的和,
故选:C.
5答案及解析:
答案:D
解析:在八大类消费中,食品烟酒、衣着、居住、交通和通信价格环比持平,另外四类价格环比均上涨,其中其他用品和服务价格环比涨幅最大,为0.4% ,生活用品及服务和医疗保健价格环比涨幅均为0. 1 % . 4月份居民消费平均价格环比涨幅为.故选 D.
6答案及解析:
答案:A
解析:设建设前总经济收入为100则建设后总经济收入为200
对于A,建设前种植收入为,建设后种植收入为故A借误:
对于B,建设前其他收入为,建设后其他收入为,故B正确
对于C,建设前养殖收入为,建设后养殖收入为,故C正确:
对于D,建设后,养殖收入占,第三产业收入占故D正确:
7答案及解析:
答案:A
解析:A项,由折线图可看出2014年9月接待的游客量小于8月接待的游客量,因此月接待游客量并不是逐月增加的,故A项结论错误符合题意.
B项,由折线图可看出2014年每个月接待的游客量小于2015年对应月份接待的游客量,2015年每个月接待的游客量小于2016年对应月份接待的游客量,所以年接待游客量逐年增加,故B项不符合题意.
C项,由折线图可看出每一年的7,8月接待的游客量远高于当年其他月份,因此各年的月接待游客量高峰期大致在7,8月,故C项不符合题意.
D项,由折线图可看出各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳,故D项不符合题意.
故本题正确答案为A.
8答案及解析:
答案:B
解析:由图可得的频率.所以圆心角.
9答案及解析:
答案:B
解析:由已知得,解得,故选B.
10答案及解析:
答案:C
解析:由已知将1000名学生分成100个组,每组10名学生,用系统抽样,46号学生被抽到,
所以第一组抽到6号,且每组抽到的学生号构成等差数列,公差,
所以,
若,则,不合题意;若,则,不合题意;
若,则,符合题意;若,则,不合题意.故选C.
11答案及解析:
答案:37; 20
解析:由分组可知,抽号的间隔为5,又因为第5组抽出的号码为22,所以第6组抽出的号码为27,第7组抽出的号码为32,第8组抽出的号码为37.
40岁以下年龄段的职工数为,则应抽取的人数为(人).
12答案及解析:
答案:20
解析:从56个学生中用系统抽样的方法抽取一个容量为4的样本,则分组时要分成4个小组,每一个小组有14人.∵学号为6,34,48的同学在样本中,即第一个学号是6,∴第二个抽取的学号是.
13答案及解析:
答案:18
解析:由频率= 以及直方图可得出分布在区间第一组与第二组共有20人,分布在区间第一组与第二组的频率分别为0.24,0.16,设总的人数为n,则,∴,所以第三小组人数为(人).
14答案及解析:
答案:(1)由频率分布直方图可知,月均用水量在的频率为.
同理,在
等组的频率分别为.
由,
解得.
(2).由(1)知, 位居民月均用水量不低于吨的频率为
.
由以上样本的频率分布,
可以估计万居民中月均用水量不低于吨的人数为
.
(3)设中位数为吨.
因为前组的频率之和为
,
而前组的频率之和为,
所以.
由,解得.
故可估计居民月均用水量的中位数为吨.
15答案及解析:
答案:(1)3(2)10.5元
解析: (1)由用水量的频率分布直方图知,该市居民该月用水量在区间,,,,内的频率依次为,所以该月用水量不超过立方米的居民占,用数量不超过立方米的居民占,依题意, 至少定为.
(2)由用水量的频率分布直方图及题意,得居民该月用水费用的数据分组与频率分布表:
组号 1 2 3 4 5 6 7 8
分组
频率 0.1 0.15 0.2 0.25 0.15 0.05 0.05 0.05
根据题意,该市居民该月的人均水费估计为: (元)
2
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
