【专题】全等三角形辅助线做法汇总 课件(14张PPT)
文档属性
| 名称 | 【专题】全等三角形辅助线做法汇总 课件(14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 732.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-07 16:38:36 | ||
图片预览


文档简介
(共14张PPT)
八年级全等三角形
辅助线的一般作法
八年级全等辅助线作法
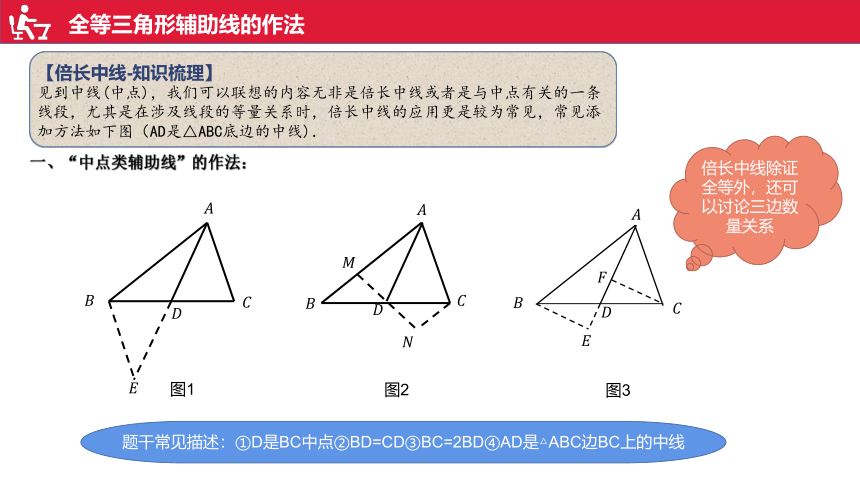
全等三角形辅助线的作法
【倍长中线-知识梳理】
见到中线(中点),我们可以联想的内容无非是倍长中线或者是与中点有关的一条线段,尤其是在涉及线段的等量关系时,倍长中线的应用更是较为常见,常见添加方法如下图(AD是△ABC底边的中线).
一、“中点类辅助线”的作法:
图1
图2
图3
题干常见描述:①D是BC中点②BD=CD③BC=2BD④AD是△ABC边BC上的中线
倍长中线除证全等外,还可以讨论三边数量关系
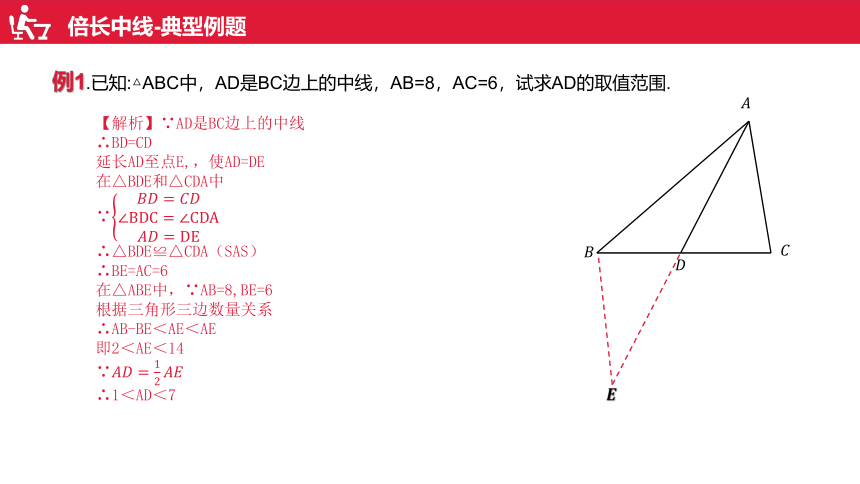
倍长中线-典型例题
例1.已知:△ABC中,AD是BC边上的中线,AB=8,AC=6,试求AD的取值范围.
【解析】∵AD是BC边上的中线
∴BD=CD
延长AD至点E,,使AD=DE
在△BDE和△CDA中
∵
∴△BDE≌△CDA(SAS)
∴BE=AC=6
在△ABE中,∵AB=8,BE=6
根据三角形三边数量关系
∴AB-BE<AE<AE
即2<AE<14
∵
∴1<AD<7
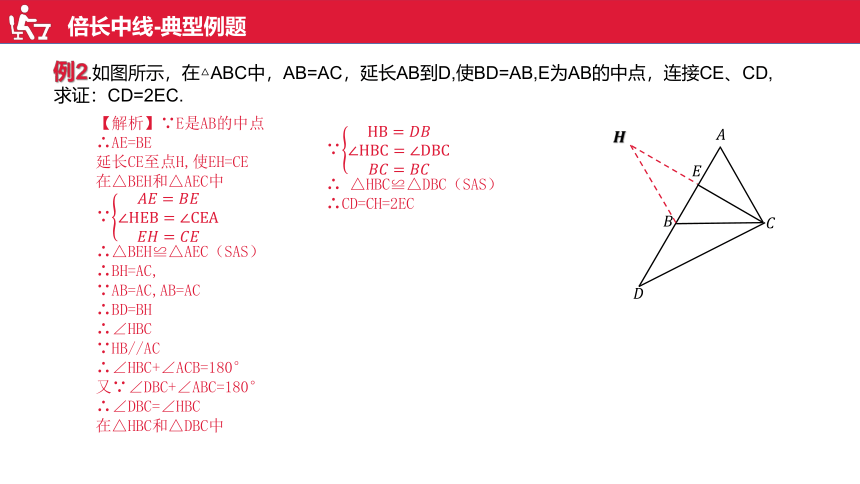
倍长中线-典型例题
例2.如图所示,在△ABC中,AB=AC,延长AB到D,使BD=AB,E为AB的中点,连接CE、CD,
求证:CD=2EC.
【解析】∵E是AB的中点
∴AE=BE
延长CE至点H,使EH=CE
在△BEH和△AEC中
∵
∴△BEH≌△AEC(SAS)
∴BH=AC,
∵AB=AC,AB=AC
∴BD=BH
∴∠HBC
∵HB//AC
∴∠HBC+∠ACB=180°
又∵∠DBC+∠ABC=180°
∴∠DBC=∠HBC
在△HBC和△DBC中
∵
∴ △HBC≌△DBC(SAS)
∴CD=CH=2EC
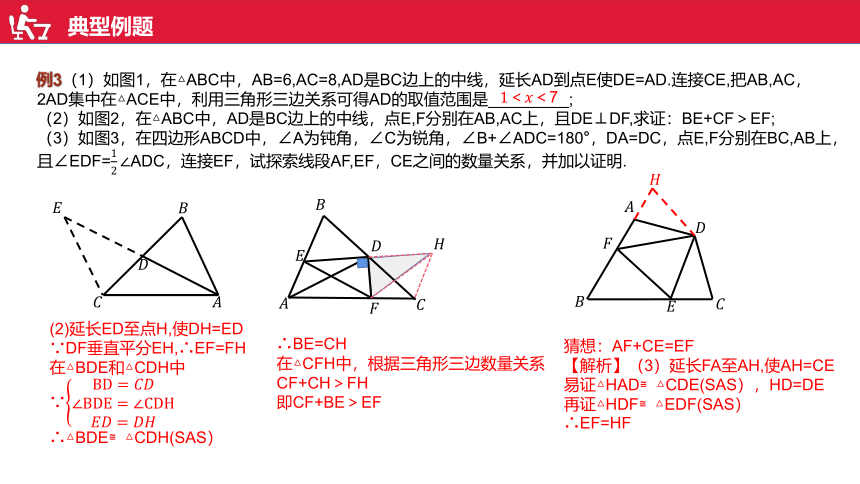
典型例题
例3(1)如图1,在△ABC中,AB=6,AC=8,AD是BC边上的中线,延长AD到点E使DE=AD.连接CE,把AB,AC,
2AD集中在△ACE中,利用三角形三边关系可得AD的取值范围是_________;
(2)如图2,在△ABC中,AD是BC边上的中线,点E,F分别在AB,AC上,且DE⊥DF,求证:BE+CF>EF;
(3)如图3,在四边形ABCD中,∠A为钝角,∠C为锐角,∠B+∠ADC=180°,DA=DC,点E,F分别在BC,AB上,
且∠EDF=ADC,连接EF,试探索线段AF,EF,CE之间的数量关系,并加以证明.
7
(2)延长ED至点H,使DH=ED
∵DF垂直平分EH,∴EF=FH
在△BDE和△CDH中
∵
∴△BDE≌△CDH(SAS)
∴BE=CH
在△CFH中,根据三角形三边数量关系
CF+CH>FH
即CF+BE>EF
猜想:AF+CE=EF
【解析】(3)延长FA至AH,使AH=CE
易证△HAD≌△CDE(SAS),HD=DE
再证△HDF≌△EDF(SAS)
∴EF=HF
全等三角形辅助线的作法
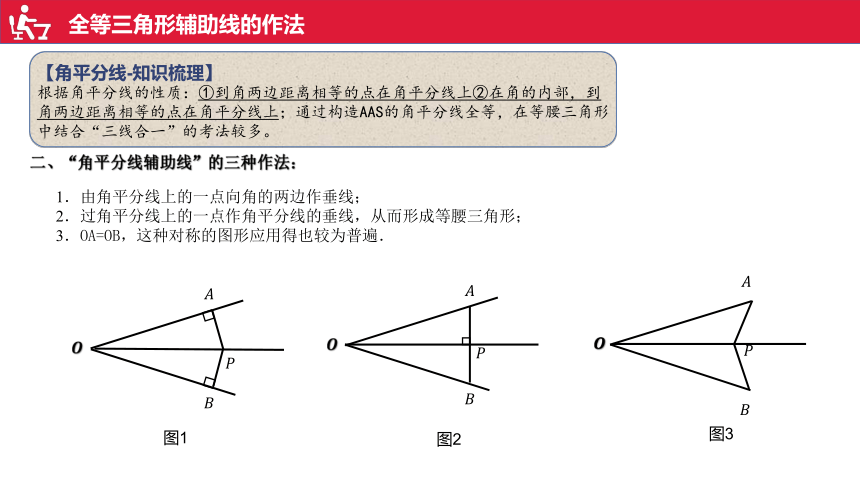
【角平分线-知识梳理】
根据角平分线的性质:①到角两边距离相等的点在角平分线上②在角的内部,到角两边距离相等的点在角平分线上;通过构造AAS的角平分线全等,在等腰三角形中结合“三线合一”的考法较多。
二、“角平分线辅助线”的三种作法:
1.由角平分线上的一点向角的两边作垂线;
2.过角平分线上的一点作角平分线的垂线,从而形成等腰三角形;
3.OA=OB,这种对称的图形应用得也较为普遍.
图1
图2
图3
全等三角形辅助线的作法
“角平分线辅助线”的应用(补充说明):
法一:如图,在△ABC中,AD平分∠BAC。在AB上截取AE=AC,连接DE。
(可以利用角平分线所在直线作对称轴,翻折三角形来构造全等三角形.)
结论:ED=CD,∠AED=∠C,∠ADE=∠ADC
法二:如图,在△ABC中, AD平分∠BAC 。延长AC到F,使AF=AB,连接DF。
(可以利用角平分线所在直线作对称轴,翻折三角形来构造全等三角形.)
结论:BD=FD,∠B=∠F,∠ADB=∠ADF
法三:在△ABC中,AD平分∠BAC。作DM⊥AB于M,DN⊥AC于N。
(还可以用“角平分线上的点到角的两边距离相等”来证DM=DN)
结论:DM=DN,AM=AN,∠ADM=∠AND
.
法1:在BC上截取BE,使BE=AB,连接DE 法2:延长BA到F,使BF=BC,连接DF
法3:作DM⊥BC于M,DN⊥BA交BA的延长线于N
典型例题
例4.已知:如图,在四边形ABC中,BD是∠ABC的角平分线,AD=CD,求证:∠A+∠C=180°
典型例题
例5 如图,已知在△ABC中,∠BAC的平分线与线段BC的垂直平分线PQ相较于点P,过点P分别作PN垂直于
AB于点N,PM垂直于AC于点M.求证:BN=CM.
∵AP平分∠BAC
∴∠NAP=∠MAP
又∵过点P分别作PN垂直于AB于点N,PM垂直于AC于点M
∴∠ANP=∠AMP=90°
在Rt△ANP和Rt△AMP中
∵
∴ Rt△ANP≌Rt△AMP(AAS)
∴NP=MP
∵PQ垂直平分BC
∴BP=PC
在Rt△BNP和Rt△CMP中
∵
∴ Rt△BNP≌Rt△CMP(HL)
∴BN=CM
典型例题
例6 在△ABC中,∠ACB=2∠B,如图①,当∠C=90°时,AD为∠BAC的平分线时,在AB上截取AE=AC,连接DE,
易证AB=AC+CD
①
②
③
(1)如图②,当∠C≠90°时,AD为△ABC的角平分线时,线段AB,AC,CD之间又有怎样的数量关系?
不需要说明理由,请直接写出你的猜想。
(2)如图③,当∠ABC≠90°时,AD为△ABC的外角平分线时,线段AB,AC,CD之间又有怎样的数量关系?
请写出你的猜想,并对你的猜想进行说明。
【解析】
(1)猜想:AB=AC+CD 证明:方法如题①,在AB上截取AE=AC。
(2)猜想:AC+AB=CD 在AF上截取AH=AC易证△ACD≌△AHD(SAS)∴CD=HD再根据∠ACB=2∠B
得∠BHD=180°-2∠B ∴△BHD为等腰三角形,HD=BH
全等三角形辅助线的作法
【截长补短-知识梳理】
初中几何常见的一种辅助线添加方式。在于“去繁从简”,体现转化与划归的数学思想;所谓“截长”,即将三者线段中最长的一段一分为二,分别等于求证的另外两条已知线段;所谓“补短”,即延长较短的线段,直至等于最长的线段
三、“截长补短辅助线”的作法:
Eq: 在正方形ABCD中,∠EDF=45°,求证AE+FC=EF
①如图1,2进行补短,构造△HDE≌△FDE(SAS)
②图3在EF上截取,使得FH=EA,FH=CF
1
2
3
例7 已知:在△ABC中,AB=AC,∠BAC=90° ,过点A作直线l,过B,C分别作BD⊥l于点D,CE⊥l于点E.
(1)如图1,当直线l在△ABC的外部时,求证:DE= BD+CE;
(2)当直线l在△ABC的内部如图2所示时,求证:DE=BD-CE;
(3)当直线l在△ABC的内部如图3所示时,直接写出DE, BD,CE三者之间的数量关系式为____________.
课堂练习
1
2
3
【解析】(1)(2)问中,利用角度的和差关系,等角的余角相等,间接求证Rt△ADB≌Rt△AEC(AAS)
DE+BD=CE
课堂练习
例8 如图所示,△ABC是边长为1的正三角形,△BDC是顶角为120°的等腰三角形,以D为顶点作一个60°的∠MDN,点M,N分别在AB,AC上,求△AMN的周长。
【解析】延长MB至点H,使BH=CN
利用同角的余角相等,易证△BDH≌△NCD(SAS)
∴HD=MD,CN=BH
再证△HDM≌△NDM(SAS)
∴MN=MH
∴AM+MN+AN=AM+MH+AN=AM+MB+BH+AN
=AB+CN+AN=AB+AC=1+1=2
课堂练习
如图,在△ABC中,AB=AC,D是三角形外一点,且∠ABD=60°,BD+DC=AB,求证:∠ACD=60°
延长BD至H,使DH=DC;易证△ADC≌△ADH(SSS)
八年级全等三角形
辅助线的一般作法
八年级全等辅助线作法
全等三角形辅助线的作法
【倍长中线-知识梳理】
见到中线(中点),我们可以联想的内容无非是倍长中线或者是与中点有关的一条线段,尤其是在涉及线段的等量关系时,倍长中线的应用更是较为常见,常见添加方法如下图(AD是△ABC底边的中线).
一、“中点类辅助线”的作法:
图1
图2
图3
题干常见描述:①D是BC中点②BD=CD③BC=2BD④AD是△ABC边BC上的中线
倍长中线除证全等外,还可以讨论三边数量关系
倍长中线-典型例题
例1.已知:△ABC中,AD是BC边上的中线,AB=8,AC=6,试求AD的取值范围.
【解析】∵AD是BC边上的中线
∴BD=CD
延长AD至点E,,使AD=DE
在△BDE和△CDA中
∵
∴△BDE≌△CDA(SAS)
∴BE=AC=6
在△ABE中,∵AB=8,BE=6
根据三角形三边数量关系
∴AB-BE<AE<AE
即2<AE<14
∵
∴1<AD<7
倍长中线-典型例题
例2.如图所示,在△ABC中,AB=AC,延长AB到D,使BD=AB,E为AB的中点,连接CE、CD,
求证:CD=2EC.
【解析】∵E是AB的中点
∴AE=BE
延长CE至点H,使EH=CE
在△BEH和△AEC中
∵
∴△BEH≌△AEC(SAS)
∴BH=AC,
∵AB=AC,AB=AC
∴BD=BH
∴∠HBC
∵HB//AC
∴∠HBC+∠ACB=180°
又∵∠DBC+∠ABC=180°
∴∠DBC=∠HBC
在△HBC和△DBC中
∵
∴ △HBC≌△DBC(SAS)
∴CD=CH=2EC
典型例题
例3(1)如图1,在△ABC中,AB=6,AC=8,AD是BC边上的中线,延长AD到点E使DE=AD.连接CE,把AB,AC,
2AD集中在△ACE中,利用三角形三边关系可得AD的取值范围是_________;
(2)如图2,在△ABC中,AD是BC边上的中线,点E,F分别在AB,AC上,且DE⊥DF,求证:BE+CF>EF;
(3)如图3,在四边形ABCD中,∠A为钝角,∠C为锐角,∠B+∠ADC=180°,DA=DC,点E,F分别在BC,AB上,
且∠EDF=ADC,连接EF,试探索线段AF,EF,CE之间的数量关系,并加以证明.
7
(2)延长ED至点H,使DH=ED
∵DF垂直平分EH,∴EF=FH
在△BDE和△CDH中
∵
∴△BDE≌△CDH(SAS)
∴BE=CH
在△CFH中,根据三角形三边数量关系
CF+CH>FH
即CF+BE>EF
猜想:AF+CE=EF
【解析】(3)延长FA至AH,使AH=CE
易证△HAD≌△CDE(SAS),HD=DE
再证△HDF≌△EDF(SAS)
∴EF=HF
全等三角形辅助线的作法
【角平分线-知识梳理】
根据角平分线的性质:①到角两边距离相等的点在角平分线上②在角的内部,到角两边距离相等的点在角平分线上;通过构造AAS的角平分线全等,在等腰三角形中结合“三线合一”的考法较多。
二、“角平分线辅助线”的三种作法:
1.由角平分线上的一点向角的两边作垂线;
2.过角平分线上的一点作角平分线的垂线,从而形成等腰三角形;
3.OA=OB,这种对称的图形应用得也较为普遍.
图1
图2
图3
全等三角形辅助线的作法
“角平分线辅助线”的应用(补充说明):
法一:如图,在△ABC中,AD平分∠BAC。在AB上截取AE=AC,连接DE。
(可以利用角平分线所在直线作对称轴,翻折三角形来构造全等三角形.)
结论:ED=CD,∠AED=∠C,∠ADE=∠ADC
法二:如图,在△ABC中, AD平分∠BAC 。延长AC到F,使AF=AB,连接DF。
(可以利用角平分线所在直线作对称轴,翻折三角形来构造全等三角形.)
结论:BD=FD,∠B=∠F,∠ADB=∠ADF
法三:在△ABC中,AD平分∠BAC。作DM⊥AB于M,DN⊥AC于N。
(还可以用“角平分线上的点到角的两边距离相等”来证DM=DN)
结论:DM=DN,AM=AN,∠ADM=∠AND
.
法1:在BC上截取BE,使BE=AB,连接DE 法2:延长BA到F,使BF=BC,连接DF
法3:作DM⊥BC于M,DN⊥BA交BA的延长线于N
典型例题
例4.已知:如图,在四边形ABC中,BD是∠ABC的角平分线,AD=CD,求证:∠A+∠C=180°
典型例题
例5 如图,已知在△ABC中,∠BAC的平分线与线段BC的垂直平分线PQ相较于点P,过点P分别作PN垂直于
AB于点N,PM垂直于AC于点M.求证:BN=CM.
∵AP平分∠BAC
∴∠NAP=∠MAP
又∵过点P分别作PN垂直于AB于点N,PM垂直于AC于点M
∴∠ANP=∠AMP=90°
在Rt△ANP和Rt△AMP中
∵
∴ Rt△ANP≌Rt△AMP(AAS)
∴NP=MP
∵PQ垂直平分BC
∴BP=PC
在Rt△BNP和Rt△CMP中
∵
∴ Rt△BNP≌Rt△CMP(HL)
∴BN=CM
典型例题
例6 在△ABC中,∠ACB=2∠B,如图①,当∠C=90°时,AD为∠BAC的平分线时,在AB上截取AE=AC,连接DE,
易证AB=AC+CD
①
②
③
(1)如图②,当∠C≠90°时,AD为△ABC的角平分线时,线段AB,AC,CD之间又有怎样的数量关系?
不需要说明理由,请直接写出你的猜想。
(2)如图③,当∠ABC≠90°时,AD为△ABC的外角平分线时,线段AB,AC,CD之间又有怎样的数量关系?
请写出你的猜想,并对你的猜想进行说明。
【解析】
(1)猜想:AB=AC+CD 证明:方法如题①,在AB上截取AE=AC。
(2)猜想:AC+AB=CD 在AF上截取AH=AC易证△ACD≌△AHD(SAS)∴CD=HD再根据∠ACB=2∠B
得∠BHD=180°-2∠B ∴△BHD为等腰三角形,HD=BH
全等三角形辅助线的作法
【截长补短-知识梳理】
初中几何常见的一种辅助线添加方式。在于“去繁从简”,体现转化与划归的数学思想;所谓“截长”,即将三者线段中最长的一段一分为二,分别等于求证的另外两条已知线段;所谓“补短”,即延长较短的线段,直至等于最长的线段
三、“截长补短辅助线”的作法:
Eq: 在正方形ABCD中,∠EDF=45°,求证AE+FC=EF
①如图1,2进行补短,构造△HDE≌△FDE(SAS)
②图3在EF上截取,使得FH=EA,FH=CF
1
2
3
例7 已知:在△ABC中,AB=AC,∠BAC=90° ,过点A作直线l,过B,C分别作BD⊥l于点D,CE⊥l于点E.
(1)如图1,当直线l在△ABC的外部时,求证:DE= BD+CE;
(2)当直线l在△ABC的内部如图2所示时,求证:DE=BD-CE;
(3)当直线l在△ABC的内部如图3所示时,直接写出DE, BD,CE三者之间的数量关系式为____________.
课堂练习
1
2
3
【解析】(1)(2)问中,利用角度的和差关系,等角的余角相等,间接求证Rt△ADB≌Rt△AEC(AAS)
DE+BD=CE
课堂练习
例8 如图所示,△ABC是边长为1的正三角形,△BDC是顶角为120°的等腰三角形,以D为顶点作一个60°的∠MDN,点M,N分别在AB,AC上,求△AMN的周长。
【解析】延长MB至点H,使BH=CN
利用同角的余角相等,易证△BDH≌△NCD(SAS)
∴HD=MD,CN=BH
再证△HDM≌△NDM(SAS)
∴MN=MH
∴AM+MN+AN=AM+MH+AN=AM+MB+BH+AN
=AB+CN+AN=AB+AC=1+1=2
课堂练习
如图,在△ABC中,AB=AC,D是三角形外一点,且∠ABD=60°,BD+DC=AB,求证:∠ACD=60°
延长BD至H,使DH=DC;易证△ADC≌△ADH(SSS)
