一元二次方程复习[上学期]
文档属性
| 名称 | 一元二次方程复习[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 654.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-12 00:00:00 | ||
图片预览








文档简介
课件22张PPT。一元二次方程
(复习课)一元二次方程一般形式解法根的判别式:根与系数的关系:应用配方法求最值问题
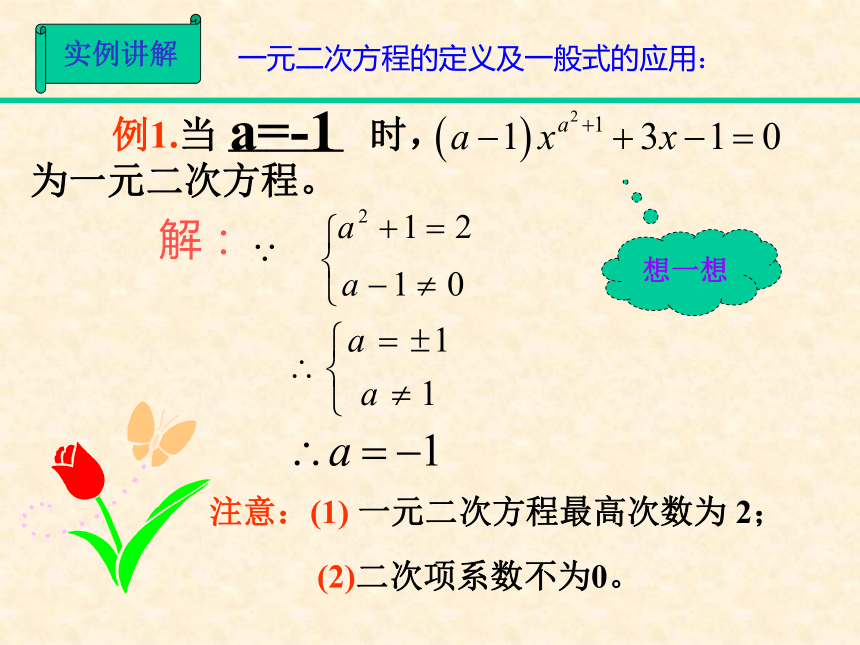
实际应用思想方法转化思想; 配方法、换元法直接开平方法配方法公式法因式分解法ax2+bx+c=0(a≠0)知识结构一元二次方程的解法 (复习)知识点1.一元二次方程的定义: 只含有一个未知数,并且未知数的最高次数为2的整式方程.2.一元二次方程的一般式:3.一元二次方程的常见解法:(1)直接开平方法(2)配方法(3)公式法(4)因式分解法一元二次方程的解法:实例讲解想一想? 例1.当 时,
为一元二次方程。解:注意:(1) 一元二次方程最高次数为 2;一元二次方程的定义及一般式的应用:(2)二次项系数不为0。———a=-1实例讲解想一想? 例2.用a、b、c表示下列一元二次方程的
二 次项系数、一次项系数和常数项解: a=3,(1) 与一元二次方程系数有关的问题都要先化为一般形式;一元二次方程的定义及一般式的应用:b=6,c=-7注意:(2)一般式右边为0。例3:解下列方程(1)实例讲解一元二次方程的解法:解: 注:当一元二次方程缺一次项时常用直接开平方法。(直接开平方法)例3:解下列方程(2)实例讲解一元二次方程的解法:解: 注:当一元二次方程二次项系数为1且一次项系数为偶数时常用配方法比较简便。(配方法)——例3:解下列方程(3)实例讲解一元二次方程的解法:解:(1)用公式法时应先将方程化为一般式;注:(2)系数包括前边的符号。(公式法)例3:解下列方程(1)实例讲解一元二次方程的解法(用适当解法):解:注:观察两边都有 宜用因式分解法。课堂练习1一元二次方程的解法例4:解下列方程(2)实例讲解一元二次方程的解法(用适当解法):解: 注:常数项绝对值较大不宜分解因式,也不易用公式法求解,却易配方,从而用配方法。例4:解下列方程(3)实例讲解一元二次方程的解法(用适当解法):解: 注:可见,化简繁,但左边两式形式相似,故考虑换元。课堂练习2一元二次方程的解法解:分析:1.2.1.2.跳跳,看看你能跳多高?用配方法证明:
例1.关于x的方程(2m2 -12m +37)x 2 +3mx+1=0,无论m取何值,此方程都是一元二次方程例2.代数式2x2-8x+9何时能取得最小值,最小值是多少?1.配方问题题型分析 例1、某商场今年2月份的营业额为400万元,3月份的营业额比2月份增加10%,5月份的营业额达到633.6万元,求3月份到5月份营业额的平均月增长率.一、增长率问题 例2、李先生将10000元存入银行一年,到期后取出2000元购买彩电,剩余8000元和利息又全部按一年定期存入银行,若存款的年利率不变,则到期后本息和是8925元,试求这种存款的年利率.(不计利息税) 例3、用12m长的一根铁丝围成长方形.
(1)如果长方形的面积为5m2,那么此时长方形的长是多少?宽是多少?如果面积是8m2呢?
(2)能否围成面积是10m2的长方形?为什么?
(3)能围成的长方形的最大面积是多少?二、面积问题 例5、某商店如果将进货价为8元的商品按每件10元售出,每天可销售200件,现采用提高售价,减少进货量的方法增加利润,如果这种商品每件涨0.5元,其销售量就会减少10件,那么,将售价定为多少时,才能使所赚利润为640元?四、销售问题 拓展:每件商品售价定为多少时,商店每天盈利最多? 2、设某人驾车正以108km/h的速度沿平直高速公路行驶,根据有关人员推算和测试,该汽车行驶时的安全距离(从刹车到车完全停止行驶的距离)为90m,
(1)从开始刹车减速到完全停止约用了多长时间?
(2)那么该车减速后平均每秒减少多少米?
(3)从开始刹车后滑行到45m处时约用了多长时间?运动与方程某军舰以20节的速度由西向东航行,一艘电子侦察船以30节的速度由南向北航行,它能侦察出周围50海里(包括50海里)范围内的目标.如图,当该军舰行至A处时,电子侦察船正位于A处的正南方向的B处,瓶AB=90海里.如果军舰和侦察船仍按原来速度沿原方向继续航行,那么航行途中侦察船能否侦察到这艘军舰 ?如果能,最早何时能侦察到?如果不能,请说明理由.运动与方程祝学有所获再
见
(复习课)一元二次方程一般形式解法根的判别式:根与系数的关系:应用配方法求最值问题
实际应用思想方法转化思想; 配方法、换元法直接开平方法配方法公式法因式分解法ax2+bx+c=0(a≠0)知识结构一元二次方程的解法 (复习)知识点1.一元二次方程的定义: 只含有一个未知数,并且未知数的最高次数为2的整式方程.2.一元二次方程的一般式:3.一元二次方程的常见解法:(1)直接开平方法(2)配方法(3)公式法(4)因式分解法一元二次方程的解法:实例讲解想一想? 例1.当 时,
为一元二次方程。解:注意:(1) 一元二次方程最高次数为 2;一元二次方程的定义及一般式的应用:(2)二次项系数不为0。———a=-1实例讲解想一想? 例2.用a、b、c表示下列一元二次方程的
二 次项系数、一次项系数和常数项解: a=3,(1) 与一元二次方程系数有关的问题都要先化为一般形式;一元二次方程的定义及一般式的应用:b=6,c=-7注意:(2)一般式右边为0。例3:解下列方程(1)实例讲解一元二次方程的解法:解: 注:当一元二次方程缺一次项时常用直接开平方法。(直接开平方法)例3:解下列方程(2)实例讲解一元二次方程的解法:解: 注:当一元二次方程二次项系数为1且一次项系数为偶数时常用配方法比较简便。(配方法)——例3:解下列方程(3)实例讲解一元二次方程的解法:解:(1)用公式法时应先将方程化为一般式;注:(2)系数包括前边的符号。(公式法)例3:解下列方程(1)实例讲解一元二次方程的解法(用适当解法):解:注:观察两边都有 宜用因式分解法。课堂练习1一元二次方程的解法例4:解下列方程(2)实例讲解一元二次方程的解法(用适当解法):解: 注:常数项绝对值较大不宜分解因式,也不易用公式法求解,却易配方,从而用配方法。例4:解下列方程(3)实例讲解一元二次方程的解法(用适当解法):解: 注:可见,化简繁,但左边两式形式相似,故考虑换元。课堂练习2一元二次方程的解法解:分析:1.2.1.2.跳跳,看看你能跳多高?用配方法证明:
例1.关于x的方程(2m2 -12m +37)x 2 +3mx+1=0,无论m取何值,此方程都是一元二次方程例2.代数式2x2-8x+9何时能取得最小值,最小值是多少?1.配方问题题型分析 例1、某商场今年2月份的营业额为400万元,3月份的营业额比2月份增加10%,5月份的营业额达到633.6万元,求3月份到5月份营业额的平均月增长率.一、增长率问题 例2、李先生将10000元存入银行一年,到期后取出2000元购买彩电,剩余8000元和利息又全部按一年定期存入银行,若存款的年利率不变,则到期后本息和是8925元,试求这种存款的年利率.(不计利息税) 例3、用12m长的一根铁丝围成长方形.
(1)如果长方形的面积为5m2,那么此时长方形的长是多少?宽是多少?如果面积是8m2呢?
(2)能否围成面积是10m2的长方形?为什么?
(3)能围成的长方形的最大面积是多少?二、面积问题 例5、某商店如果将进货价为8元的商品按每件10元售出,每天可销售200件,现采用提高售价,减少进货量的方法增加利润,如果这种商品每件涨0.5元,其销售量就会减少10件,那么,将售价定为多少时,才能使所赚利润为640元?四、销售问题 拓展:每件商品售价定为多少时,商店每天盈利最多? 2、设某人驾车正以108km/h的速度沿平直高速公路行驶,根据有关人员推算和测试,该汽车行驶时的安全距离(从刹车到车完全停止行驶的距离)为90m,
(1)从开始刹车减速到完全停止约用了多长时间?
(2)那么该车减速后平均每秒减少多少米?
(3)从开始刹车后滑行到45m处时约用了多长时间?运动与方程某军舰以20节的速度由西向东航行,一艘电子侦察船以30节的速度由南向北航行,它能侦察出周围50海里(包括50海里)范围内的目标.如图,当该军舰行至A处时,电子侦察船正位于A处的正南方向的B处,瓶AB=90海里.如果军舰和侦察船仍按原来速度沿原方向继续航行,那么航行途中侦察船能否侦察到这艘军舰 ?如果能,最早何时能侦察到?如果不能,请说明理由.运动与方程祝学有所获再
见
同课章节目录
