一元二次方程复习课[上学期]
文档属性
| 名称 | 一元二次方程复习课[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 27.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-13 19:38:00 | ||
图片预览


文档简介
一元二次方程复习课
设计:许滨 审核:黄亚军 姓名
1.一元二次方程的概念
方程中只含一个未知数,并且未知数最高次数是二次,这样的整式方程叫一元二次方程。下列方程是一元二次方程吗?为什么?
①2x2-3x+1=0 ②x2+y+2=3x ③ ④(2x+1)2-(4x+1)(x+1)=2
2.一元二次方程的解
能够使方程左右两边相等的未知数的值叫方程的解,这与一元一次方程,二元一次方程的解的意义一样。
判断方程后面的数是否是方程的解:
(1)2x2-3x+1=0 (,1) (2)x2-=0 () (3)(2x-1)2=3 ()
例1.求出下列方程二次项,一次项及常数项:(1)6x2=5x+2,(2)(3x-1)(x+2)=
例2.如图所示,要建一个面积为130平方米的仓库,仓库的 一边靠墙(墙长16米)并在与墙平行的一边开一道1米宽的门,现有能围成32米长的木板,求仓库的长和宽,对于这个问题,你能列出方程吗?试着求其解来,并与同伴交流一下自己的心得。
3.直接开平方法解一元二次方程.
对于形如x2=m或(ax+n)2=m(a≠0,m≥0)的型的一元二次方程,即一元二次方程的一边是含有未知数的一次式的平方,而另一边是一个非负数,可用直接开平方法求解.
因为负数没有平方根,所以当m<0时,x2=m或(ax+n)2=m无解
你能解下列方程吗 并结合自己解方程的过程与结果探索方程的解的情况.
① ②(3x-1)2=0 ③
4.运用配方法解一元二次方程
通过配方的方法把一元二次方程转化成形如(ax+b)2=m的形式,再运用直接开平方的方法求解.用配方法解一元二次方程的步骤如下:
(1)把方程中含有未知数的项移到方程的左边,常数项移到方程的右边.
(2)根据等式的性质把二次项的系数化为1.
(3)把方程两边都加上一次项系数一半的平方,使左边配成一个完全平方式.
这时,方程右边如果是一个非负数,就可直接用开平方的方法求出它的解,如果方程右边是负数,则这个方程无解.
5.运用求根公式解一元二次方程。
运用公式解一元二次方程的步骤:(1)将方程化为一元二次方程一般形式。(2)确定a、b、c的值。(3)求出b2-4ac的值,确定方程是否有实根.(4)代入求根公式求根。
例3.运用求根公式解下列方程:
(1)5x2=3x (2)x2-+2=0 (3)(y-1)(y+3)+5=0
例4.已知一个直角三角形的两直角边的长恰当方程2x2-8x+7=0的两个根,则这个直角三角形的斜边长是
A. B.3 C.6 D.9
6.因式分解法解一元二次方程的根据:
如果两个因式的积等于0,那么这两个因式至少有一个为0,反过来,如果两个因式中有一个因式为0那么它们之积为0.
例如: (2-7x)(5x-3)=0,则 或
因式分解法解一元二次方程的方法及步骤:
(1)将方程的右边化为0;(2)把方程的左边分解为两个一次因式的积;(3)令每个因式为0,得到两个一元一次方程;(4)解这两个一元一次方程得原方程的解.
例5.用因式分解法解下列方程:
(1)(2x-1)2+3(1-2x)=0 (2)(1-3x)2=16(2x+3)2 (3)x2+6x-7=0
7.建立一元二次方程模型解决实际问题
列一元二次方程解应用题步骤:
(1)审题:弄清题意,找出已知量和未知量,并分清数量关系,明确所求的量.
(2)设出未知数,根据题意,设出合适的未知数,根据所设未知数,列出有关的代数式.
(3)分析等量关系:即找到能反映全部意义的相等关系.
(4)列方程:根据等量关系列出方程。
(5)解方程
(6)检验:检验所求得的解是否符合题意,正确取舍。
(7)写出答案
例6.某商店如果将进货为8元的商品每件10元售出,每天可销售200件,通过一段时间的摸索,该店主发现这种商品每涨价0.5元,其销售量就减少10件,每降价0.5元,其销售量就增加10件.
(1)你能帮助店主设计一种方案,使每天的利润达到700元吗
(2)将售价定为每价多少元时,能使这天所获利润最大 最大利润是多少
例7.某网络公司2000年各项经营收入中,经营电脑配件收入600万元,占全部经营总收入的40%,该公司预计2002年经营总收入达到2160万元,且计划从2000到2002年每年经营总收入的年增长率相同,问2001年的预计经营总收入为多少万元
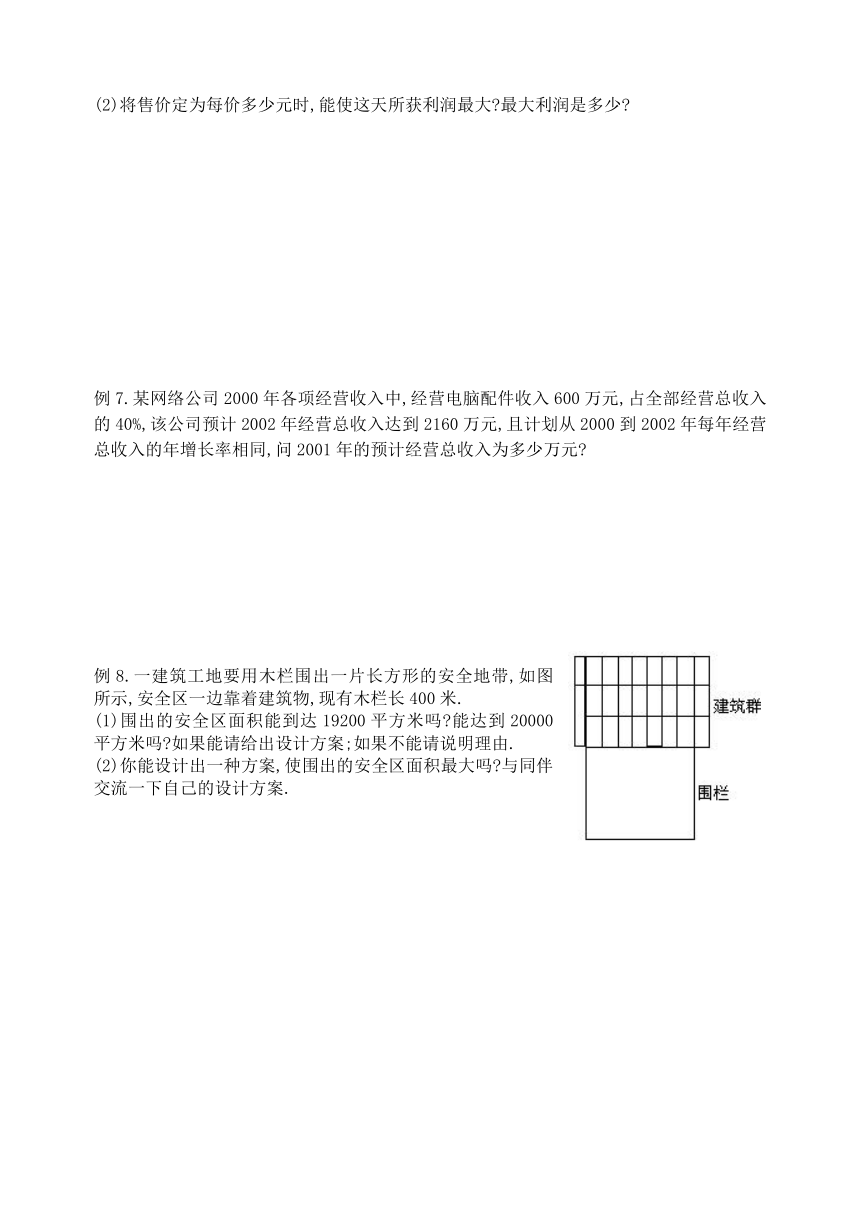
例8.一建筑工地要用木栏围出一片长方形的安全地带,如图所示,安全区一边靠着建筑物,现有木栏长400米.
(1)围出的安全区面积能到达19200平方米吗 能达到20000平方米吗 如果能请给出设计方案;如果不能请说明理由.
(2)你能设计出一种方案,使围出的安全区面积最大吗 与同伴交流一下自己的设计方案.
课堂练习
一、选择题。
1.关于x的一元二次方程2mx2-x+m2=0有一根为-1,则m的值应为
A.1,-1 B.-1 C.1 D.
2.方程(x+1)2-2=0的根是
A. B.
C. D.
3.若x2-mx+是一个完全平方式,则m=
A.1 B.-1 C.±1 D.以上均不对
4.方程(x-2)2=(3-2x)2可化为
A.x-2=3-2x B.x-2=2x-3
C.x-2=3-2x或x-2=2x-3 D.以上均不对
5.对于二次三项式2x2+4x+5的值,下列叙述正确的是
A.一定为正数 B.可为正数,也可能为负数
C.一定为负数 D.其值的符号与x值有关
6.若代数式4x2-2x-5与2x2+1的值互为相反数,则x的值为
A.1或 B.1或 C.-1或 D.1或
7.利用求根公式求的根时,a,b,c的值分别是
A.5, ,6 B.5,6, C.5,-6, D.5,-6,-
8.对于一元二次方程ax2+bx+c=0,下列叙述正确的是
A.方程总有两个实数根 B.只有当b2-4ac≥0时,才有两实根
C.当b2-4ac<0时,方程只有一个实根 D.当b2-4ac=0时,方程无实根
9.已知三角形两边长分别是1和2,第三边的长为2x2-5x+3=0的根,则这个三角形的周长是
A.4 B. C.4或 D.不存在
10.某超市一月份的营业额为200万元,一,二,三月份的营业额为1000万元,设平均每月的营业额为增长率为x,则由题意列方程为
A.200+200×2x=1000 B.200(1+x)2=1000
C.200+200×3x=1000 D.200[1+(1+x)+(1+x)2]=1000
11.北京市政府为迎接2008年奥运会,决定改善城市面貌,绿化环境,计划经过两年时间,绿地面积增加44%,则这两年平均每年绿地面积的增长率是
A.19% B.20% C.21% D.25%
二、填空题。
12.① =(x- )2 ② =(x+ )2
13.某种手表的成本在两年内以100元降低到81元,那么平均每年降低成本的百分率是 .
14.请写出一个一元二次方程,使其没有实数根,你写的方程是
15.已知(x2+y2+1)2=4,则x2+y2=
16.有一间长20米,宽15米的会议室,在它的中间铺一块地毯,地毯的面积是会议室面积的 ,四周未铺地毯的留空宽度相同,则留空的宽度为
三、解答题。
17.一次会议上,每两个参加会议的人都相互握了一次手,有人统计一共握了210次手,你能根据上述提供的信息求出参加此次会议的有多少人吗
18.要建一个面积为150m2的长方形养鸡场,为了节约材料,鸡场的一边靠着原有的一堵墙,墙长为a米,另三边用竹篱笆围成,如果篱笆长为35米
(1)你能求出鸡场的长与宽吗 试试看. (2)题中的墙的长度a对解题有什么作用.
19.某商场销售一批名牌衬衫,平均每天可以售出20件,每件盈利40元,为了扩大销售,增加利润,尽量减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫降价1元,商场平均每天多售出2件,若商场平均每天要盈利1200元,每件衬衫应降价多少元
20.某儿童玩具商店将进货价为30元的一种玩具以40元售出,平均每月能售出600个.调查表明:这种玩具售价每上涨1元,其销售量将减少10个,为了实现平均每月12000元的销售利润,这种玩具的售价应定为多少 这时进这种玩具多少个
21.据2001年中国环境状况公报,我国由水蚀和风蚀造成的水土流失面积达356万平方公里,其中风蚀造成水土流失面积比水蚀造成的水土流失面积多26万平方公里.(1)问水蚀,风蚀造成的水土流失面积各是多少平方公里 (2)西北某省重视水土流失问题,2001年治理了水土流失面积400平方公里,该省逐年加大治理力度,计划今明两年治理水土流失面积都比前一年增长 一个相同的百分数,到2003年底,使这三年治理水土流失面积达到1324平方公里,求该省今明两年治理水土流失面积每年增长的百分数.
22.某玩具厂生产一种玩具熊猫,每日最高产量为40只,且每日产出的产品全部售出,已知生产x只玩具熊猫的成本为R(元),售价为每只P(元),且R,P与x的关系式为R=500+30x,P=170-2x,当日产量为多少时,每日获得的利润为1750元
23.某公司向银行贷款20万元资金,约定两年到期时一次性还本付息,利息是本金的12%,该公司利用这笔贷款经营,两年到期时除还清贷款的本金及利息外,还盈余6.4万元,若在经营期间每一年比前一年资金增长百分数相同,试求出这个百分数.
24.宏达汽车租货公司共有出租车120辆,每辆汽车的日租金为160元,出租业务天\天供不应求,为适应市场需求,经有关部门批准,公司准备适当提高日租金,经市场调查发现,一辆汽车日租金每增加10元,每天出租的汽车相应地减少6辆.若不考虑其它因素,公司将每辆汽车的日租金提高几个10元 (1)能使公司的日租金总收入达到19380元 (2)使公司的日租金总收入最高 最高是多少
25.某商场第一年初投入50万元进行商品经营,以后每年年终将当年获得的年利润与当年年初投入资金相加所得的总资金,作为下一年年初投入资金继续进行经营.
(1)如果第一年的年利率为p,则第一年年终的总金可用代数式表示为 万元.
(2)如果第二年的年获利率比第一年的年获利率多10个百分点,第二年年终的总资金为66万元,求第一年的年获利率.
设计:许滨 审核:黄亚军 姓名
1.一元二次方程的概念
方程中只含一个未知数,并且未知数最高次数是二次,这样的整式方程叫一元二次方程。下列方程是一元二次方程吗?为什么?
①2x2-3x+1=0 ②x2+y+2=3x ③ ④(2x+1)2-(4x+1)(x+1)=2
2.一元二次方程的解
能够使方程左右两边相等的未知数的值叫方程的解,这与一元一次方程,二元一次方程的解的意义一样。
判断方程后面的数是否是方程的解:
(1)2x2-3x+1=0 (,1) (2)x2-=0 () (3)(2x-1)2=3 ()
例1.求出下列方程二次项,一次项及常数项:(1)6x2=5x+2,(2)(3x-1)(x+2)=
例2.如图所示,要建一个面积为130平方米的仓库,仓库的 一边靠墙(墙长16米)并在与墙平行的一边开一道1米宽的门,现有能围成32米长的木板,求仓库的长和宽,对于这个问题,你能列出方程吗?试着求其解来,并与同伴交流一下自己的心得。
3.直接开平方法解一元二次方程.
对于形如x2=m或(ax+n)2=m(a≠0,m≥0)的型的一元二次方程,即一元二次方程的一边是含有未知数的一次式的平方,而另一边是一个非负数,可用直接开平方法求解.
因为负数没有平方根,所以当m<0时,x2=m或(ax+n)2=m无解
你能解下列方程吗 并结合自己解方程的过程与结果探索方程的解的情况.
① ②(3x-1)2=0 ③
4.运用配方法解一元二次方程
通过配方的方法把一元二次方程转化成形如(ax+b)2=m的形式,再运用直接开平方的方法求解.用配方法解一元二次方程的步骤如下:
(1)把方程中含有未知数的项移到方程的左边,常数项移到方程的右边.
(2)根据等式的性质把二次项的系数化为1.
(3)把方程两边都加上一次项系数一半的平方,使左边配成一个完全平方式.
这时,方程右边如果是一个非负数,就可直接用开平方的方法求出它的解,如果方程右边是负数,则这个方程无解.
5.运用求根公式解一元二次方程。
运用公式解一元二次方程的步骤:(1)将方程化为一元二次方程一般形式。(2)确定a、b、c的值。(3)求出b2-4ac的值,确定方程是否有实根.(4)代入求根公式求根。
例3.运用求根公式解下列方程:
(1)5x2=3x (2)x2-+2=0 (3)(y-1)(y+3)+5=0
例4.已知一个直角三角形的两直角边的长恰当方程2x2-8x+7=0的两个根,则这个直角三角形的斜边长是
A. B.3 C.6 D.9
6.因式分解法解一元二次方程的根据:
如果两个因式的积等于0,那么这两个因式至少有一个为0,反过来,如果两个因式中有一个因式为0那么它们之积为0.
例如: (2-7x)(5x-3)=0,则 或
因式分解法解一元二次方程的方法及步骤:
(1)将方程的右边化为0;(2)把方程的左边分解为两个一次因式的积;(3)令每个因式为0,得到两个一元一次方程;(4)解这两个一元一次方程得原方程的解.
例5.用因式分解法解下列方程:
(1)(2x-1)2+3(1-2x)=0 (2)(1-3x)2=16(2x+3)2 (3)x2+6x-7=0
7.建立一元二次方程模型解决实际问题
列一元二次方程解应用题步骤:
(1)审题:弄清题意,找出已知量和未知量,并分清数量关系,明确所求的量.
(2)设出未知数,根据题意,设出合适的未知数,根据所设未知数,列出有关的代数式.
(3)分析等量关系:即找到能反映全部意义的相等关系.
(4)列方程:根据等量关系列出方程。
(5)解方程
(6)检验:检验所求得的解是否符合题意,正确取舍。
(7)写出答案
例6.某商店如果将进货为8元的商品每件10元售出,每天可销售200件,通过一段时间的摸索,该店主发现这种商品每涨价0.5元,其销售量就减少10件,每降价0.5元,其销售量就增加10件.
(1)你能帮助店主设计一种方案,使每天的利润达到700元吗
(2)将售价定为每价多少元时,能使这天所获利润最大 最大利润是多少
例7.某网络公司2000年各项经营收入中,经营电脑配件收入600万元,占全部经营总收入的40%,该公司预计2002年经营总收入达到2160万元,且计划从2000到2002年每年经营总收入的年增长率相同,问2001年的预计经营总收入为多少万元
例8.一建筑工地要用木栏围出一片长方形的安全地带,如图所示,安全区一边靠着建筑物,现有木栏长400米.
(1)围出的安全区面积能到达19200平方米吗 能达到20000平方米吗 如果能请给出设计方案;如果不能请说明理由.
(2)你能设计出一种方案,使围出的安全区面积最大吗 与同伴交流一下自己的设计方案.
课堂练习
一、选择题。
1.关于x的一元二次方程2mx2-x+m2=0有一根为-1,则m的值应为
A.1,-1 B.-1 C.1 D.
2.方程(x+1)2-2=0的根是
A. B.
C. D.
3.若x2-mx+是一个完全平方式,则m=
A.1 B.-1 C.±1 D.以上均不对
4.方程(x-2)2=(3-2x)2可化为
A.x-2=3-2x B.x-2=2x-3
C.x-2=3-2x或x-2=2x-3 D.以上均不对
5.对于二次三项式2x2+4x+5的值,下列叙述正确的是
A.一定为正数 B.可为正数,也可能为负数
C.一定为负数 D.其值的符号与x值有关
6.若代数式4x2-2x-5与2x2+1的值互为相反数,则x的值为
A.1或 B.1或 C.-1或 D.1或
7.利用求根公式求的根时,a,b,c的值分别是
A.5, ,6 B.5,6, C.5,-6, D.5,-6,-
8.对于一元二次方程ax2+bx+c=0,下列叙述正确的是
A.方程总有两个实数根 B.只有当b2-4ac≥0时,才有两实根
C.当b2-4ac<0时,方程只有一个实根 D.当b2-4ac=0时,方程无实根
9.已知三角形两边长分别是1和2,第三边的长为2x2-5x+3=0的根,则这个三角形的周长是
A.4 B. C.4或 D.不存在
10.某超市一月份的营业额为200万元,一,二,三月份的营业额为1000万元,设平均每月的营业额为增长率为x,则由题意列方程为
A.200+200×2x=1000 B.200(1+x)2=1000
C.200+200×3x=1000 D.200[1+(1+x)+(1+x)2]=1000
11.北京市政府为迎接2008年奥运会,决定改善城市面貌,绿化环境,计划经过两年时间,绿地面积增加44%,则这两年平均每年绿地面积的增长率是
A.19% B.20% C.21% D.25%
二、填空题。
12.① =(x- )2 ② =(x+ )2
13.某种手表的成本在两年内以100元降低到81元,那么平均每年降低成本的百分率是 .
14.请写出一个一元二次方程,使其没有实数根,你写的方程是
15.已知(x2+y2+1)2=4,则x2+y2=
16.有一间长20米,宽15米的会议室,在它的中间铺一块地毯,地毯的面积是会议室面积的 ,四周未铺地毯的留空宽度相同,则留空的宽度为
三、解答题。
17.一次会议上,每两个参加会议的人都相互握了一次手,有人统计一共握了210次手,你能根据上述提供的信息求出参加此次会议的有多少人吗
18.要建一个面积为150m2的长方形养鸡场,为了节约材料,鸡场的一边靠着原有的一堵墙,墙长为a米,另三边用竹篱笆围成,如果篱笆长为35米
(1)你能求出鸡场的长与宽吗 试试看. (2)题中的墙的长度a对解题有什么作用.
19.某商场销售一批名牌衬衫,平均每天可以售出20件,每件盈利40元,为了扩大销售,增加利润,尽量减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫降价1元,商场平均每天多售出2件,若商场平均每天要盈利1200元,每件衬衫应降价多少元
20.某儿童玩具商店将进货价为30元的一种玩具以40元售出,平均每月能售出600个.调查表明:这种玩具售价每上涨1元,其销售量将减少10个,为了实现平均每月12000元的销售利润,这种玩具的售价应定为多少 这时进这种玩具多少个
21.据2001年中国环境状况公报,我国由水蚀和风蚀造成的水土流失面积达356万平方公里,其中风蚀造成水土流失面积比水蚀造成的水土流失面积多26万平方公里.(1)问水蚀,风蚀造成的水土流失面积各是多少平方公里 (2)西北某省重视水土流失问题,2001年治理了水土流失面积400平方公里,该省逐年加大治理力度,计划今明两年治理水土流失面积都比前一年增长 一个相同的百分数,到2003年底,使这三年治理水土流失面积达到1324平方公里,求该省今明两年治理水土流失面积每年增长的百分数.
22.某玩具厂生产一种玩具熊猫,每日最高产量为40只,且每日产出的产品全部售出,已知生产x只玩具熊猫的成本为R(元),售价为每只P(元),且R,P与x的关系式为R=500+30x,P=170-2x,当日产量为多少时,每日获得的利润为1750元
23.某公司向银行贷款20万元资金,约定两年到期时一次性还本付息,利息是本金的12%,该公司利用这笔贷款经营,两年到期时除还清贷款的本金及利息外,还盈余6.4万元,若在经营期间每一年比前一年资金增长百分数相同,试求出这个百分数.
24.宏达汽车租货公司共有出租车120辆,每辆汽车的日租金为160元,出租业务天\天供不应求,为适应市场需求,经有关部门批准,公司准备适当提高日租金,经市场调查发现,一辆汽车日租金每增加10元,每天出租的汽车相应地减少6辆.若不考虑其它因素,公司将每辆汽车的日租金提高几个10元 (1)能使公司的日租金总收入达到19380元 (2)使公司的日租金总收入最高 最高是多少
25.某商场第一年初投入50万元进行商品经营,以后每年年终将当年获得的年利润与当年年初投入资金相加所得的总资金,作为下一年年初投入资金继续进行经营.
(1)如果第一年的年利率为p,则第一年年终的总金可用代数式表示为 万元.
(2)如果第二年的年获利率比第一年的年获利率多10个百分点,第二年年终的总资金为66万元,求第一年的年获利率.
同课章节目录
