高中数学必修第一册人教A版(2019)4.2《指数函数的图象和性质》名师课件(共38张PPT)
文档属性
| 名称 | 高中数学必修第一册人教A版(2019)4.2《指数函数的图象和性质》名师课件(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-05 16:50:39 | ||
图片预览






文档简介
(共38张PPT)
复习引入
指数函数的概念
定义:形式定义
结构特征
系数
底数
指数
函数叫做指数函数,其中x是自变量,函数的定义域是R.
指数函数的概念
复习引入
人教A版同步教材名师课件
指数函数的图象和性质
学习目标
学 习 目 标 核心素养
通过画指数函数的图象,初步掌握指数函数的性质 直观想象
利用函数的单调性比较大小、解不等式 逻辑推理
课程目标
1、掌握指数函数的图象和性质,培养学生实际应用函数的能力;
2、通过观察图象,分析、归纳、总结指数函数的性质;
3、在指数函数的学习过程中,体验数学的科学价值并养成勇于探索的良好习惯.
数学学科素养
1.数学抽象:指数函数的图像与性质;
2.逻辑推理:图像平移问题;
3.数学运算:求函数的定义域与值域;
4.数据分析:利用指数函数的性质比较两个函数值的大小:
5.数学建模:通过由抽象到具体,由具体到一般的数形结合思想总结指数函数性质.
学习目标
研究初等函数性质的基本方法和步骤:
描点法
1、画出函数图象
2、研究函数性质
探究新知
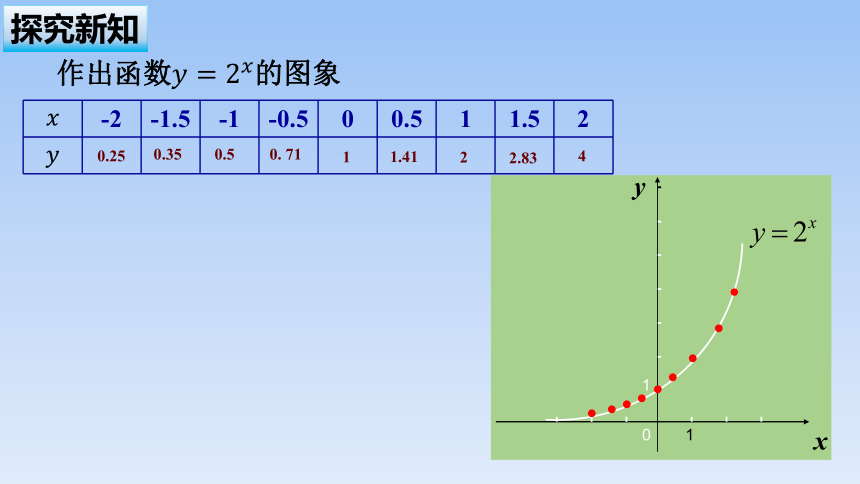
-2 -1.5 -1 -0.5 0 0.5 1 1.5 2
作出函数的图象
0
1
1
.
.
.
.
.
.
.
.
.
0.35
0.25
0. 71
4
2
2.83
1
1.41
0.5
探究新知
0
1
1
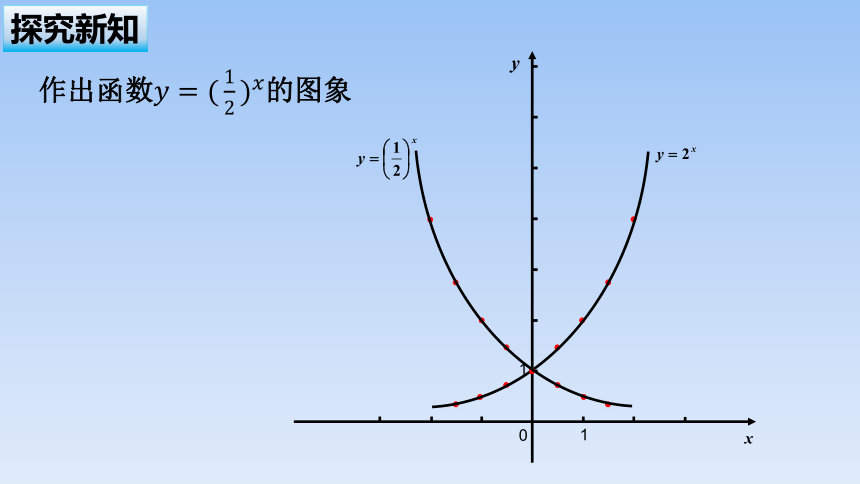
作出函数的图象
探究新知
0
1
1
探究新知
0
1
1
0
1
1
0
1
0
1
探究新知
y
x
0
· (0,1)
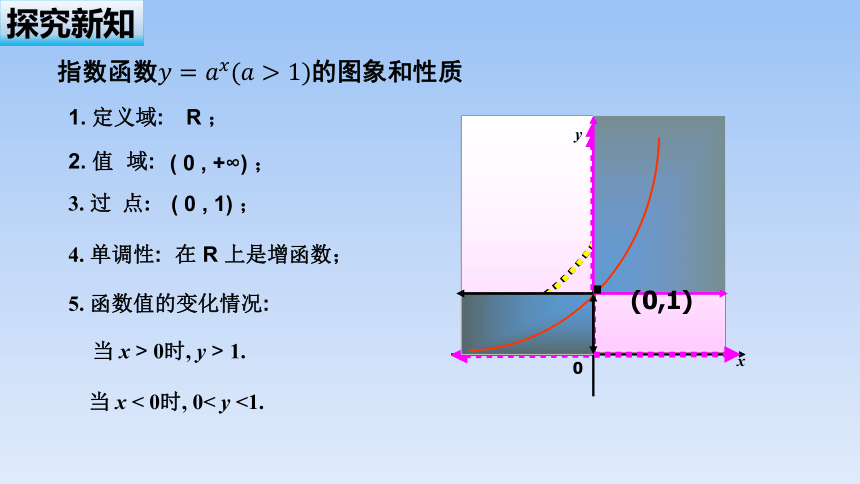
指数函数的图象和性质
1. 定义域:
2. 值 域:
3. 过 点:
4. 单调性:
5. 函数值的变化情况:
当 x < 0时, 0< y <1.
R ;
( 0 , +∞) ;
( 0 , 1) ;
在 R 上是增函数;
当 x > 0时, y > 1.
探究新知
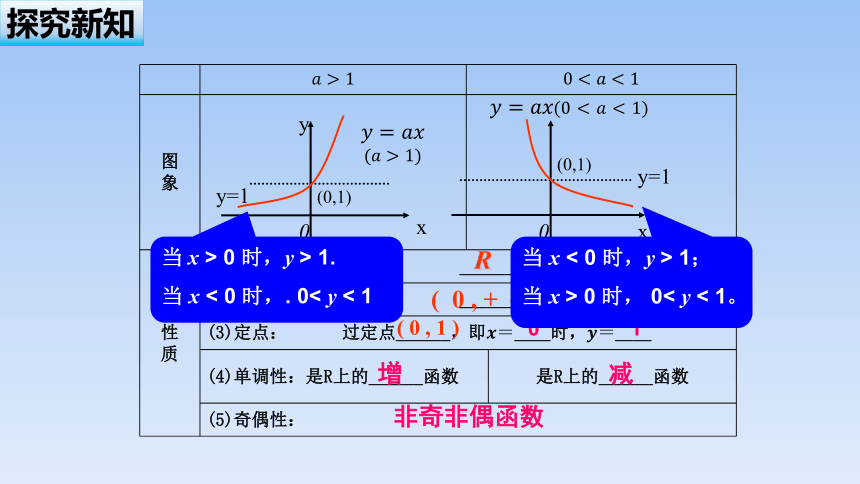
图 象
性 质 (1)定义域: ______
(2)值域: ______
(3)定点: 过定点______,即____时,____
(4)单调性:是R上的______函数 是R上的______函数
(5)奇偶性:
y
x
0
y=1
(0,1)
x
(0,1)
y=1
0
R
( 0 , + ∞ )
( 0 , 1 )
0
1
增
减
非奇非偶函数
当 x > 0 时,y > 1.
当 x < 0 时,. 0< y < 1
当 x < 0 时,y > 1;
当 x > 0 时, 0< y < 1。
探究新知
指数函数性质
左右无限上无天,
永于横轴不沾边,
大1增,小1减,
图像恒过(0,1)点.
探究新知
0
1
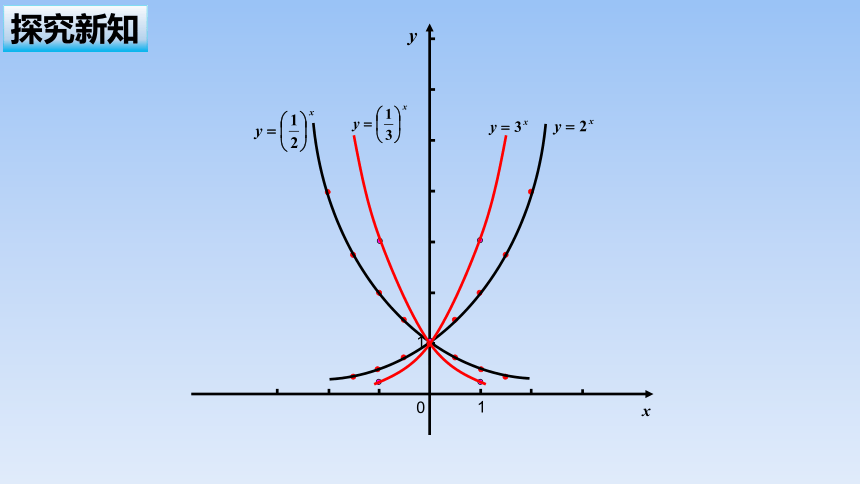
在第一象限当取同一个数值时,函数值随底数的增大而增大
底数互为倒数,图象关于轴对称
观察图象特征与底数关系:
探究新知
典例讲解
例1、求下列函数的定义域和值域:
(1) ;(2) ;(3)
解析
(1)由得,
∴函数的定义域为, , 的值域为
(2)要使函数有意义,则,解得,
∴函数的定义域为.
, 即函数的值域为.
典例讲解
例1、求下列函数的定义域和值域:
(1) ;(2) ;(3)
解析
(3)易知函数的定义域为R.
又, 函数的值域为(0,16].
方法归纳
求指数型函数的定义域时,先观察函数是还是型(且).
(1)由于指数函数的定义域是R,所以函数的定义域与的定义域相同.
(2)的定义域与函数的定义域不一定相同.函数的定义域为[0,+∞),而的定义域为R.求的定义域时,应由的定义域与的值域的等价性,建立关于的不等式,利用指数函数的相关性质求解.
(3)求型函数的定义域时,往往转化为解指数不等式(组)
求指数型函数的定义域的一般方法
变式训练
1.求函数的定义域.
解析
要使函数有意义,则应满足
在R上是增函数,
.
故所求函数的定义域为.
典例讲解
例2、已知函数在[-1,1]上有最大值14,求的值.
解析
令则原函数可化为,其图象的对称轴为
当>1时,因为,所以又上单调递增,
所以,解得=3或= 5(舍去).
当0< <1时,因为,所以,又在上单调递增,
所以,解得= 或= (舍去).
综上可知, 的值为3或
利用换元法,令,构造关于的一元二次函数,再配方求最值,让其最大值为14,构建与有关的方程,进而求得的值.
分析
方法归纳
(1)指数型函数的值域问题一般可分为两类:一类是型,求这类复合函数的值域,应先求出的取值范围,再由指数函数的单调性来确定其值域;另一类是型的复合函数,求这类复合函数的值域,应先令,求出的范围,再结合确定的值域即可.
(2)求函数的值域仍应坚持“定义域优先”的原则.
变式训练
2.函数的值域是( )
解析
令则
B
变式训练
3.当时,函数的最小值为______.
解析
,
,
时,函数有最小值,且.
故函数
典例讲解
例3、比较下列各组中两个值的大小.
(1) ;(2) (3)
解析
(1)∵ , 函数在定义域R上单调递减,又,
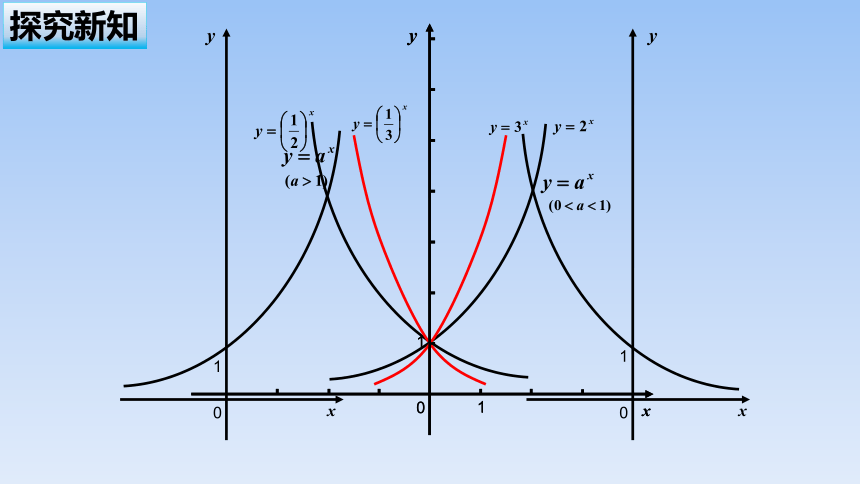
(2)在同一平面直角坐标系中画出指数函数的图象,如图所示.
当时,由图象观察可得.
典例讲解
例3、比较下列各组中两个值的大小.
(1) ;(2) (3)
解析
(3)∵
指数函数在定义域R上均是减函数,且在区间(0,+∞)上函数的图象在函数的图象的下方,
.
又指数函数在R上是减函数,可得
.
典例讲解
例3、比较下列各组中两个值的大小.
(1) ;(2) (3)
解析
(3)∵指数函数在定义域R上均是减函数,且在区间(0,+∞)上函数的图象在函数的图象的下方, .
又根据指数函数在R上是减函数可得.
.
方法归纳
比较幂值大小的三种类型及处理方法
变式训练
4.比较下列各组中两个数的大小:
(1) ;(2)
解析
(1)构造函数在上是增函数.
.
(2)分别构造函数,
上分别为增函数和减函数.
,
.
典例讲解
例4、函数在上的最大值比最小值大,求的值.
解析
分情况讨论:
①当时,函数在[1,2]上的最大值为,最小值为,解得或(舍去).
②当时,函数上的最大值为,最小值为,解得(舍去)
综上所述,
方法归纳
指数函数在定义域R上是单调函数,因此在R的子集上也是单调函数,在区间的两个端点处分别取到最大值和最小值.应特别注意的是,当底数未知时,要对底数分情况讨论.
变式训练
5.已知函数在区间[1,2]上有最大值9和最小值1.
(1)求的值;
(2)若不等式在上有解,求实数的取值范围.
解析
(1)令,
对应图象的对称轴为直线,
, 解得.
(2)由(1)知上有解,
.
故实数的取值范围为
典例讲解
例5、(1)解不等式
(2)已知,求的取值范围.
解析
(1) , 原不等式可转化为
在R上是减函数, 故原不等式的解集是
(2)分情况讨论:
①当时,函数在R上是减函数,
,解得或.
②当时,函数在R上是增函数,
综上所述,当时,的取值范围是
当时,的取值范围是.
方法归纳
指数不等式的类型及求解时应注意的问题
(1)形如的不等式,借助于函数的单调性求解,如果的取值不确定,要对分和两种情况讨论.
(2)形如的不等式,注意将转化为以为底数的指数幂的形式,再借助函数的单调性求解.
(3)形如的不等式,可利用函数图象求解.
变式训练
解析
6.(1)已知,求实数的取值范围;
(2)求不等式的解集.
(1)
(2)当时,由,解得;
当时,由,解得.
综上所述,当时,此不等式的解集为,
当时,此不等式的解集为.
当堂练习
1、已知,则指数函数① ,②的大致图象为( )
C
当堂练习
2、若函数是实数集R上的增函数,则实数的取值范围为( )
A、
3、若函数是指数函数,则的值为( )
A、2 B、-2
B
D
当堂练习
4、函数的定义域为( )
= ( )
A
C
归纳小结
指数函数的性质
定义域 R
单调性
值域
过定点(0,1)
增函数,>1
减函数,0<<1
作 业
P118练习:1、2、3
复习引入
指数函数的概念
定义:形式定义
结构特征
系数
底数
指数
函数叫做指数函数,其中x是自变量,函数的定义域是R.
指数函数的概念
复习引入
人教A版同步教材名师课件
指数函数的图象和性质
学习目标
学 习 目 标 核心素养
通过画指数函数的图象,初步掌握指数函数的性质 直观想象
利用函数的单调性比较大小、解不等式 逻辑推理
课程目标
1、掌握指数函数的图象和性质,培养学生实际应用函数的能力;
2、通过观察图象,分析、归纳、总结指数函数的性质;
3、在指数函数的学习过程中,体验数学的科学价值并养成勇于探索的良好习惯.
数学学科素养
1.数学抽象:指数函数的图像与性质;
2.逻辑推理:图像平移问题;
3.数学运算:求函数的定义域与值域;
4.数据分析:利用指数函数的性质比较两个函数值的大小:
5.数学建模:通过由抽象到具体,由具体到一般的数形结合思想总结指数函数性质.
学习目标
研究初等函数性质的基本方法和步骤:
描点法
1、画出函数图象
2、研究函数性质
探究新知
-2 -1.5 -1 -0.5 0 0.5 1 1.5 2
作出函数的图象
0
1
1
.
.
.
.
.
.
.
.
.
0.35
0.25
0. 71
4
2
2.83
1
1.41
0.5
探究新知
0
1
1
作出函数的图象
探究新知
0
1
1
探究新知
0
1
1
0
1
1
0
1
0
1
探究新知
y
x
0
· (0,1)
指数函数的图象和性质
1. 定义域:
2. 值 域:
3. 过 点:
4. 单调性:
5. 函数值的变化情况:
当 x < 0时, 0< y <1.
R ;
( 0 , +∞) ;
( 0 , 1) ;
在 R 上是增函数;
当 x > 0时, y > 1.
探究新知
图 象
性 质 (1)定义域: ______
(2)值域: ______
(3)定点: 过定点______,即____时,____
(4)单调性:是R上的______函数 是R上的______函数
(5)奇偶性:
y
x
0
y=1
(0,1)
x
(0,1)
y=1
0
R
( 0 , + ∞ )
( 0 , 1 )
0
1
增
减
非奇非偶函数
当 x > 0 时,y > 1.
当 x < 0 时,. 0< y < 1
当 x < 0 时,y > 1;
当 x > 0 时, 0< y < 1。
探究新知
指数函数性质
左右无限上无天,
永于横轴不沾边,
大1增,小1减,
图像恒过(0,1)点.
探究新知
0
1
在第一象限当取同一个数值时,函数值随底数的增大而增大
底数互为倒数,图象关于轴对称
观察图象特征与底数关系:
探究新知
典例讲解
例1、求下列函数的定义域和值域:
(1) ;(2) ;(3)
解析
(1)由得,
∴函数的定义域为, , 的值域为
(2)要使函数有意义,则,解得,
∴函数的定义域为.
, 即函数的值域为.
典例讲解
例1、求下列函数的定义域和值域:
(1) ;(2) ;(3)
解析
(3)易知函数的定义域为R.
又, 函数的值域为(0,16].
方法归纳
求指数型函数的定义域时,先观察函数是还是型(且).
(1)由于指数函数的定义域是R,所以函数的定义域与的定义域相同.
(2)的定义域与函数的定义域不一定相同.函数的定义域为[0,+∞),而的定义域为R.求的定义域时,应由的定义域与的值域的等价性,建立关于的不等式,利用指数函数的相关性质求解.
(3)求型函数的定义域时,往往转化为解指数不等式(组)
求指数型函数的定义域的一般方法
变式训练
1.求函数的定义域.
解析
要使函数有意义,则应满足
在R上是增函数,
.
故所求函数的定义域为.
典例讲解
例2、已知函数在[-1,1]上有最大值14,求的值.
解析
令则原函数可化为,其图象的对称轴为
当>1时,因为,所以又上单调递增,
所以,解得=3或= 5(舍去).
当0< <1时,因为,所以,又在上单调递增,
所以,解得= 或= (舍去).
综上可知, 的值为3或
利用换元法,令,构造关于的一元二次函数,再配方求最值,让其最大值为14,构建与有关的方程,进而求得的值.
分析
方法归纳
(1)指数型函数的值域问题一般可分为两类:一类是型,求这类复合函数的值域,应先求出的取值范围,再由指数函数的单调性来确定其值域;另一类是型的复合函数,求这类复合函数的值域,应先令,求出的范围,再结合确定的值域即可.
(2)求函数的值域仍应坚持“定义域优先”的原则.
变式训练
2.函数的值域是( )
解析
令则
B
变式训练
3.当时,函数的最小值为______.
解析
,
,
时,函数有最小值,且.
故函数
典例讲解
例3、比较下列各组中两个值的大小.
(1) ;(2) (3)
解析
(1)∵ , 函数在定义域R上单调递减,又,
(2)在同一平面直角坐标系中画出指数函数的图象,如图所示.
当时,由图象观察可得.
典例讲解
例3、比较下列各组中两个值的大小.
(1) ;(2) (3)
解析
(3)∵
指数函数在定义域R上均是减函数,且在区间(0,+∞)上函数的图象在函数的图象的下方,
.
又指数函数在R上是减函数,可得
.
典例讲解
例3、比较下列各组中两个值的大小.
(1) ;(2) (3)
解析
(3)∵指数函数在定义域R上均是减函数,且在区间(0,+∞)上函数的图象在函数的图象的下方, .
又根据指数函数在R上是减函数可得.
.
方法归纳
比较幂值大小的三种类型及处理方法
变式训练
4.比较下列各组中两个数的大小:
(1) ;(2)
解析
(1)构造函数在上是增函数.
.
(2)分别构造函数,
上分别为增函数和减函数.
,
.
典例讲解
例4、函数在上的最大值比最小值大,求的值.
解析
分情况讨论:
①当时,函数在[1,2]上的最大值为,最小值为,解得或(舍去).
②当时,函数上的最大值为,最小值为,解得(舍去)
综上所述,
方法归纳
指数函数在定义域R上是单调函数,因此在R的子集上也是单调函数,在区间的两个端点处分别取到最大值和最小值.应特别注意的是,当底数未知时,要对底数分情况讨论.
变式训练
5.已知函数在区间[1,2]上有最大值9和最小值1.
(1)求的值;
(2)若不等式在上有解,求实数的取值范围.
解析
(1)令,
对应图象的对称轴为直线,
, 解得.
(2)由(1)知上有解,
.
故实数的取值范围为
典例讲解
例5、(1)解不等式
(2)已知,求的取值范围.
解析
(1) , 原不等式可转化为
在R上是减函数, 故原不等式的解集是
(2)分情况讨论:
①当时,函数在R上是减函数,
,解得或.
②当时,函数在R上是增函数,
综上所述,当时,的取值范围是
当时,的取值范围是.
方法归纳
指数不等式的类型及求解时应注意的问题
(1)形如的不等式,借助于函数的单调性求解,如果的取值不确定,要对分和两种情况讨论.
(2)形如的不等式,注意将转化为以为底数的指数幂的形式,再借助函数的单调性求解.
(3)形如的不等式,可利用函数图象求解.
变式训练
解析
6.(1)已知,求实数的取值范围;
(2)求不等式的解集.
(1)
(2)当时,由,解得;
当时,由,解得.
综上所述,当时,此不等式的解集为,
当时,此不等式的解集为.
当堂练习
1、已知,则指数函数① ,②的大致图象为( )
C
当堂练习
2、若函数是实数集R上的增函数,则实数的取值范围为( )
A、
3、若函数是指数函数,则的值为( )
A、2 B、-2
B
D
当堂练习
4、函数的定义域为( )
= ( )
A
C
归纳小结
指数函数的性质
定义域 R
单调性
值域
过定点(0,1)
增函数,>1
减函数,0<<1
作 业
P118练习:1、2、3
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
