高中数学必修第一册人教A版(2019)4.2.2《指数函数的图象和性质---习题课》名师课件(共35张PPT)
文档属性
| 名称 | 高中数学必修第一册人教A版(2019)4.2.2《指数函数的图象和性质---习题课》名师课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-05 16:51:26 | ||
图片预览











文档简介
(共35张PPT)
人教A版同步教材名师课件
指数函数的图象和性质
---习题课
一、指数函数的图象
二、指数型函数的单调区间
三、指数方程的解法
四、指数函数的综合问题
一、指数函数的图象
典例讲解
例1、函数的图象可能是 ( )
解析
若>1,则0<<1,所以在R上是增函数,且图象可以由的图象向下平移个单位长度得到,其中0<<1,因此选项A,B排除;若0<<1,则>1,所以在R上是减函数,且图象可以由的图象向下平移个单位长度得到,其中>1,故排除选项C,选项D正确.
D
方法归纳
函数图象识辨的求解思路
(1)根据图象“上升”或“下降”确定底数>1或0< <1;
(2)在轴右侧,指数函数的图象从下到上相应的底数由小到大;在轴左侧,指数函数的图象从下到上相应的底数由大到小;
(3)根据“左加右减,上加下减”的原则,确定图象的平移变换,从而确定指数型函数的图象与两坐标轴的交点位置.
变式训练
1.二次函数与指数函数的图象可能是 ( )
解析
二次函数的方程是其图象的顶点坐标为,由各选项中指数函数的图象知,再观察四个选项,只有A中的二次函数图象的顶点的横坐标在和0之间.
A
典例讲解
例2、函数的图象过定点______.
解析
解法一:因为指数函数的图象过定点(0,1),所以在函数中,令,得,得,即函数的图象过定点(3,4)
解法二:将原函数解析式变形,得,把看作的指数函数,所以当时,,解得所以原函数的图象过定点(3,4).
令,得定点的横坐标,进而求得函数值,即得定点的纵坐标.
(3,4)
思路分析
方法归纳
指数函数的图象过定点(0,1),据此可解决形如的函数图象过定点的问题,即令,得,则函数图象过定点.
变式训练
2.已知函数的图象恒过定点A,则点A的坐标为_____.
解析
+1=2,
所以函数的图象恒过定点A(2,2).
(2,2)
典例讲解
例3、若函数的图象在第一、三、四象限,则必有( )
A. B. C. D.
解析
由指数函数的图象知函数的图象在第一、二象限,且恒过点(0,1),而函数的图象是由的图象向上或向下平移个单位长度得到的.故若函数的图象在第一、三、四象限,则,且,∴ ,b>0.
D
方法归纳
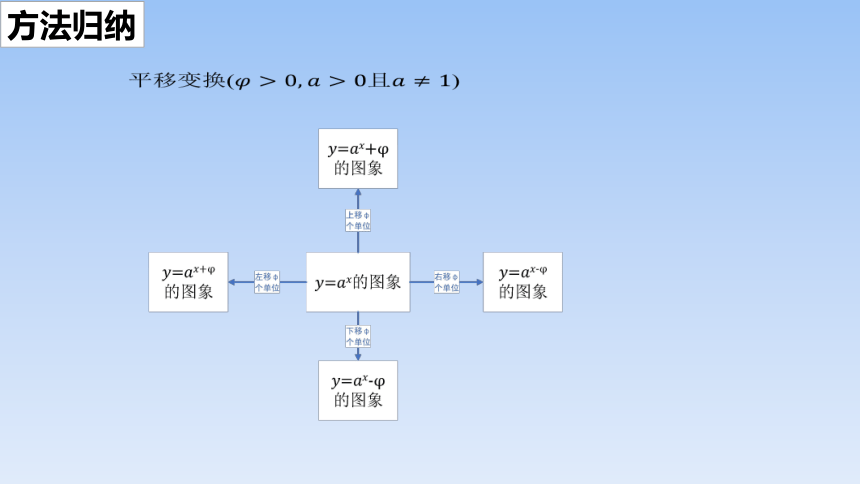
平移变换(且)
变式训练
3.为了得到函数的图象,只需把函数图象上所有的点( )
A、向右平移3个单位长度,再向下平移1个单位长度
B、向左平移3个单位长度,再向下平移1个单位长度
C、向右平移3个单位长度,再向上平移1个单位长度
D、向左平移3个单位长度,再向上平移1个单位长度
解析
把函数的图象向右平移3个单位长度,得到函数的图象,将所得的图象向下平移1个单位长度,得到函数 1的图象.
A
典例讲解
例4、画出函数的图象,并根据图象求函数的单调区间.
解析
,的图象如图所示
由图象可得函数的单调递增区间为(-∞,0],单调递减区间为(0,+∞).
先去绝对值符号化为分段函数,再画出分段函数的图象,从而求得函数的单调区间.
思路分析
方法归纳
翻折变换
变式训练
4.函数的图象是( )
解析
易知是偶函数,先画出时的图象,再作关于轴对称的图象.
C
典例讲解
例5、画出下列函数的图象,并说明它们是由函数的图象经过怎样的变换得到的.
(1);(2);(3)
解析
(1) 的图象是由的图象作关于轴对称的图象得到的,如图1
(2) 的图象是由的图象作关于轴对称的图象得到的,如图2
(3) 的图象是由的图象作关于原点对称的图象得到的,如图3
方法归纳
对称变换
典例讲解
例6、在平面直角坐标系中,若直线与函数的图象只有1个交点,则实数的取值范围是____________________________.
解析
画出函数的图象,如图所示:
若直线与函数的图象只有1个交点,则或,即实数的取值范围是
方法归纳
函数的图象广泛应用于解题过程中,利用数形结合的思想解题可以把数学关系(代数关系)与几何图形有机地结合起来,从而充分地显示条件与结论的内在联系,达到“以形助数,以数解形”的目的,数形结合的思想常常用于解方程,解不等式,求函数的值域、单调性,求参数的取值范围.
变式训练
5、若直线与函数)的图象有两个交点,则的取值范围是_____.
解析
当时,函数的图象如图(1)所示,要使直线与的图象有两个交点, .
当时,函数的图象如图(2)所示,由于,所以直线的图象有一个交点,故的取值范围为
二、指数型函数的单调区间
典例讲解
例7、求函数的值域与单调区间.
解析
定义域为R,故在上是增函数,在上是减函数,又为减函数,所以根据复合函数的“同增异减”得上是减函数,在(1,+∞)上是增函数,所以值域为,单调递增区间为,单调递减区间为.
用换元法将其化为指数函数,利用指数函数的图象与性质及复合函数的单调性与值域的求法求解.
思路
分析
方法归纳
(1)对于形如的函数的单调性,可将函数转化为函数与函数的复合,再利用复合函数的单调性法则来处理.
(2)对于形如的复合函数的单调性,可令,利用内层函数及外层函数的单调性来确定函数的单调性.
以上
变式训练
解析
6.求函数的单调区间.
令,则在上单调递减,在上单调递增,且为R上的减函数,故函数的单调增区间为,单调减区间为.
三、指数方程的解法
典例讲解
例8、解下列方程
解析
.
(2)则方程可化为,解得
(1)观察方程可知:等号两边可化成同底的指数式,利用指数相等解方程.(2)先将等式变形,再利用换元法求解.
思路
分析
方法归纳
指数方程的类型
(1)形如的方程化为求解;
(2)形如的方程,用换元法求解.
变式训练
解析
7.解下列方程:
.
.
(3)令,则原方程可化为
四、指数函数的综合问题
典例讲解
例9、已知函数
(1)讨论函数的奇偶性;
(2)证明: >0
解析
(1)由已知得,则定义域为(-∞,0)∪(0,+∞),定义域关于原点对称.
所以函数为偶函数.
(2)证明:当 ,因而,由于函数为偶函数,则当
方法归纳
指数函数综合问题的解题策略
指数函数是一种基本初等函数,常与第一章学习的函数的单调性、奇偶性等知识点融合在一起,此时按照求解函数的单调性、奇偶性的办法分析、解决问题即可.
指数函数是非奇非偶函数,但与指数函数有关且具有奇偶性的函数也是常见的与指数函数有关的函数的奇偶性问题主要是通过奇偶性定义来求解,其难点在于指数式的化简与变形,比如函数的奇偶性.
变式训练
8.已知函数且).
(1)判断函数的奇偶性;
(2)当求实数的取值范围.
解析
(1)由题可知函数的定义域为R, ,
为R上的奇函数
.
典例讲解
例10、已知,
(1)求函数的定义域和值域;
(2)讨论函数的单调性.
解析
(1)由题意,可得的定义域为R.
,
(2)解法一: 在R上为增函数;
同理,当时,在R上为减函数.
典例讲解
例10、已知,
(1)求函数的定义域和值域;
(2)讨论函数的单调性.
解析
(1)由题意,可得的定义域为R.
,
(2)解法二:由(1)知为增函数, 同理, 在R上为减函数.
变式训练
9.设是定义在R上的偶函数.
(1)求的值;
(2)证明:上是增函数.
解析
(1)依题意,对一切
对一切恒成立.由此可得∴ =1.
(2)证明:任取,则 . ,,
,上是增函数.
人教A版同步教材名师课件
指数函数的图象和性质
---习题课
一、指数函数的图象
二、指数型函数的单调区间
三、指数方程的解法
四、指数函数的综合问题
一、指数函数的图象
典例讲解
例1、函数的图象可能是 ( )
解析
若>1,则0<<1,所以在R上是增函数,且图象可以由的图象向下平移个单位长度得到,其中0<<1,因此选项A,B排除;若0<<1,则>1,所以在R上是减函数,且图象可以由的图象向下平移个单位长度得到,其中>1,故排除选项C,选项D正确.
D
方法归纳
函数图象识辨的求解思路
(1)根据图象“上升”或“下降”确定底数>1或0< <1;
(2)在轴右侧,指数函数的图象从下到上相应的底数由小到大;在轴左侧,指数函数的图象从下到上相应的底数由大到小;
(3)根据“左加右减,上加下减”的原则,确定图象的平移变换,从而确定指数型函数的图象与两坐标轴的交点位置.
变式训练
1.二次函数与指数函数的图象可能是 ( )
解析
二次函数的方程是其图象的顶点坐标为,由各选项中指数函数的图象知,再观察四个选项,只有A中的二次函数图象的顶点的横坐标在和0之间.
A
典例讲解
例2、函数的图象过定点______.
解析
解法一:因为指数函数的图象过定点(0,1),所以在函数中,令,得,得,即函数的图象过定点(3,4)
解法二:将原函数解析式变形,得,把看作的指数函数,所以当时,,解得所以原函数的图象过定点(3,4).
令,得定点的横坐标,进而求得函数值,即得定点的纵坐标.
(3,4)
思路分析
方法归纳
指数函数的图象过定点(0,1),据此可解决形如的函数图象过定点的问题,即令,得,则函数图象过定点.
变式训练
2.已知函数的图象恒过定点A,则点A的坐标为_____.
解析
+1=2,
所以函数的图象恒过定点A(2,2).
(2,2)
典例讲解
例3、若函数的图象在第一、三、四象限,则必有( )
A. B. C. D.
解析
由指数函数的图象知函数的图象在第一、二象限,且恒过点(0,1),而函数的图象是由的图象向上或向下平移个单位长度得到的.故若函数的图象在第一、三、四象限,则,且,∴ ,b>0.
D
方法归纳
平移变换(且)
变式训练
3.为了得到函数的图象,只需把函数图象上所有的点( )
A、向右平移3个单位长度,再向下平移1个单位长度
B、向左平移3个单位长度,再向下平移1个单位长度
C、向右平移3个单位长度,再向上平移1个单位长度
D、向左平移3个单位长度,再向上平移1个单位长度
解析
把函数的图象向右平移3个单位长度,得到函数的图象,将所得的图象向下平移1个单位长度,得到函数 1的图象.
A
典例讲解
例4、画出函数的图象,并根据图象求函数的单调区间.
解析
,的图象如图所示
由图象可得函数的单调递增区间为(-∞,0],单调递减区间为(0,+∞).
先去绝对值符号化为分段函数,再画出分段函数的图象,从而求得函数的单调区间.
思路分析
方法归纳
翻折变换
变式训练
4.函数的图象是( )
解析
易知是偶函数,先画出时的图象,再作关于轴对称的图象.
C
典例讲解
例5、画出下列函数的图象,并说明它们是由函数的图象经过怎样的变换得到的.
(1);(2);(3)
解析
(1) 的图象是由的图象作关于轴对称的图象得到的,如图1
(2) 的图象是由的图象作关于轴对称的图象得到的,如图2
(3) 的图象是由的图象作关于原点对称的图象得到的,如图3
方法归纳
对称变换
典例讲解
例6、在平面直角坐标系中,若直线与函数的图象只有1个交点,则实数的取值范围是____________________________.
解析
画出函数的图象,如图所示:
若直线与函数的图象只有1个交点,则或,即实数的取值范围是
方法归纳
函数的图象广泛应用于解题过程中,利用数形结合的思想解题可以把数学关系(代数关系)与几何图形有机地结合起来,从而充分地显示条件与结论的内在联系,达到“以形助数,以数解形”的目的,数形结合的思想常常用于解方程,解不等式,求函数的值域、单调性,求参数的取值范围.
变式训练
5、若直线与函数)的图象有两个交点,则的取值范围是_____.
解析
当时,函数的图象如图(1)所示,要使直线与的图象有两个交点, .
当时,函数的图象如图(2)所示,由于,所以直线的图象有一个交点,故的取值范围为
二、指数型函数的单调区间
典例讲解
例7、求函数的值域与单调区间.
解析
定义域为R,故在上是增函数,在上是减函数,又为减函数,所以根据复合函数的“同增异减”得上是减函数,在(1,+∞)上是增函数,所以值域为,单调递增区间为,单调递减区间为.
用换元法将其化为指数函数,利用指数函数的图象与性质及复合函数的单调性与值域的求法求解.
思路
分析
方法归纳
(1)对于形如的函数的单调性,可将函数转化为函数与函数的复合,再利用复合函数的单调性法则来处理.
(2)对于形如的复合函数的单调性,可令,利用内层函数及外层函数的单调性来确定函数的单调性.
以上
变式训练
解析
6.求函数的单调区间.
令,则在上单调递减,在上单调递增,且为R上的减函数,故函数的单调增区间为,单调减区间为.
三、指数方程的解法
典例讲解
例8、解下列方程
解析
.
(2)则方程可化为,解得
(1)观察方程可知:等号两边可化成同底的指数式,利用指数相等解方程.(2)先将等式变形,再利用换元法求解.
思路
分析
方法归纳
指数方程的类型
(1)形如的方程化为求解;
(2)形如的方程,用换元法求解.
变式训练
解析
7.解下列方程:
.
.
(3)令,则原方程可化为
四、指数函数的综合问题
典例讲解
例9、已知函数
(1)讨论函数的奇偶性;
(2)证明: >0
解析
(1)由已知得,则定义域为(-∞,0)∪(0,+∞),定义域关于原点对称.
所以函数为偶函数.
(2)证明:当 ,因而,由于函数为偶函数,则当
方法归纳
指数函数综合问题的解题策略
指数函数是一种基本初等函数,常与第一章学习的函数的单调性、奇偶性等知识点融合在一起,此时按照求解函数的单调性、奇偶性的办法分析、解决问题即可.
指数函数是非奇非偶函数,但与指数函数有关且具有奇偶性的函数也是常见的与指数函数有关的函数的奇偶性问题主要是通过奇偶性定义来求解,其难点在于指数式的化简与变形,比如函数的奇偶性.
变式训练
8.已知函数且).
(1)判断函数的奇偶性;
(2)当求实数的取值范围.
解析
(1)由题可知函数的定义域为R, ,
为R上的奇函数
.
典例讲解
例10、已知,
(1)求函数的定义域和值域;
(2)讨论函数的单调性.
解析
(1)由题意,可得的定义域为R.
,
(2)解法一: 在R上为增函数;
同理,当时,在R上为减函数.
典例讲解
例10、已知,
(1)求函数的定义域和值域;
(2)讨论函数的单调性.
解析
(1)由题意,可得的定义域为R.
,
(2)解法二:由(1)知为增函数, 同理, 在R上为减函数.
变式训练
9.设是定义在R上的偶函数.
(1)求的值;
(2)证明:上是增函数.
解析
(1)依题意,对一切
对一切恒成立.由此可得∴ =1.
(2)证明:任取,则 . ,,
,上是增函数.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
